Формулировка задач оптимизации в терминах математического программирования предполагает, прежде, всего, четкую классификацию параметров, на которых построены математические модели оптимизируемых объектов. При этом различают три характерные группы параметров.
1. Конструктивные параметры. Это независимые друг от друга (или слабо зависимые, взаимной зависимостью которых можно пренебречь) конструктивно настраиваемые, переменные. В процессе проектирования стремятся выбрать численные значения этих параметров так, чтобы наилучшим образом удовлетворить техническим требованиям, предъявляемым к конструкции. Указанные переменные, таким образом, можно изменять воздействуя тем самым па выходные свойства проектируемой конструкции в желаемом направлении. На конструктивные параметры, как правило, накладываются двусторонние ограничения, обусловленные конструктивно-компоновочной, технологической или эксплуатационной осуществимостью проектируемого объекта.
2. Параметры состояния. Это выходные свойства конструкции, ее отклик. Они характеризуют поведение. объекта. Параметры состояния регламентируются техническими требованиями. Последние представляются в виде односторонних или двусторонних ограничений на параметры состояния.
3. Параметры внешней среды. Это независимые друг от друга (или слабо зависимые, взаимной зависимостью которых можно пренебречь) параметры, характеризующие среду, в которой протекает жизненный цикл проектируемого объекта. Параметры среды, так же, как и конструктивные параметры, определяют его поведение. Параметры среды обычно задаются на некотором интервале в виде двусторонних ограничений. К числу подобного рода параметров относят и промежуток времени, в котором развиваются анализируемые процессы, режимы функционирования объекта и т. п. Одной из особенностей свойств внешней среды является то, что они могут быть случайными факторами. В процессе анализа поведения конструкции пытаются найти такие значения параметров внешней среды, при которых конструкция проявляет свои предельные состояния.
Конструктивно-настраиваемые параметры и параметры состояния определяют объект проектирования, а параметры среды — внешние условия, в которых этот объект находится.
Обозначим вектором х=(  ) —конструктивно-настраиваемые параметры, вектором g =
) —конструктивно-настраиваемые параметры, вектором g =  ) — параметры состояния, а вектором у=
) — параметры состояния, а вектором у=  ) —параметры среды, где п, m, l — общее число учитываемых параметров.
) —параметры среды, где п, m, l — общее число учитываемых параметров.
Поскольку конструктивно-настраиваемые параметры и внешние факторы играют роль независимых переменных, а параметры состояния зависимы от них, то для детерминированных моделей функционирования проектируемого объекта g = g(x), а для стохастических моделей вероятностной природы g = g(x, у). При этом в задачах параметрического синтеза в роли параметров управления (оптимизируемых параметров) выступают конструктивно-настраиваемые переменные х, а в задачах анализа — переменные внешней среды у.
Нахождение наилучшего решения при детермированном синтезе конструкции связано с решением задачи математического программирования: найти такие значения конструктивно-настраиваемых параметров  которые минимизируют или максимизируют критерий (целевую функцию) Q (
которые минимизируют или максимизируют критерий (целевую функцию) Q (  ) в области R, определяемой ограничениями.
) в области R, определяемой ограничениями.
min {Q(x): gt(x) < О, i = 1, т;  , j = 1, п}.
, j = 1, п}.
Здесь  значения j-й управляемой переменной, характеризующие область ее возможных изменений.
значения j-й управляемой переменной, характеризующие область ее возможных изменений.
Эта задача относится к классу задач нелинейного невыпуклого программирования, поскольку Q(x) и g(x) в моделях функционирования орудий представляются обычно неявными нелинейными, невыпуклыми (многоэкстремальными) функциями параметров х.
Как уже отмечалось, задача синтеза конструкции сопряжена с поиском наилучших решений одновременно по нескольким противоречивым показателям Qi(x). Оптимизация по каждому из них приводит к различным значениям управляемых переменных х. Векторный критерий оптимальности Q (х) = ( 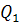 (x),...,
(x),...,  (x)) приходится при этом свертывать, конструируя с помощью приведенных ранее компромиссов скалярные функции Q(x) = f(Ql(x),..., Qn(x)).
(x)) приходится при этом свертывать, конструируя с помощью приведенных ранее компромиссов скалярные функции Q(x) = f(Ql(x),..., Qn(x)).
Рассмотрим, на примере аддитивного критерия возможные подходы к объединению частных критериев в обобщенный скалярный критерий. Для количественно соизмеримых критериев обобщенный скалярный критерий получается как взвешенная сумма:
Q(x)= 
Где 
Размерность весовых коэффициентов  такова, что в числителе стоит общая размерность, а в знаменателе — размерность соответствующего критерия
такова, что в числителе стоит общая размерность, а в знаменателе — размерность соответствующего критерия  .
.
В некоторых случаях целесообразно сравнивать между собой не критерии оптимальности, а потери по каждому из них. Потерн вводятся как разность между значениями  и его оптимальной величиной:
и его оптимальной величиной:
Qk* = min  , x
, x 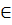 R.
R.
В этом случае аддитивный критерий имеет вид
Q(x)= 
В первом случае Q(x) объединяет частные критерии в одной размерности, а во втором случае приводит эти критерии, кроме того, и к общему началу отсчета.
Недостатком метода взвешенных сумм является то, что компромиссное решение, оптимальное по критерию Q{x), может оказаться неудовлетворительным по некоторым из частных критериев  . В связи с этим приходится вводить дополнительные ограничения на частные критерии:
. В связи с этим приходится вводить дополнительные ограничения на частные критерии:  . Тогда определение эффективного вектора оптимизируемых параметров сведется к решению задачи нелинейного программирования:
. Тогда определение эффективного вектора оптимизируемых параметров сведется к решению задачи нелинейного программирования:
minQ(x) 
где p — число ограничений на частные критерии.
Выбор весовых коэффициентов  может быть основан на физических представлениях, предпочтении частных критериев по важности, экспертной оценке и, вообще говоря, связан с наличием определенного опыта и экспериментальной проверки.
может быть основан на физических представлениях, предпочтении частных критериев по важности, экспертной оценке и, вообще говоря, связан с наличием определенного опыта и экспериментальной проверки.
При отсутствии информации о важности частных критериев можно предположить, что они равноценны. Это позволяет в качестве обобщенного критерия использовать сумму относительных отклонений частных критериев от их оптимальных значений:
Q(x)= 
В этом случае обеспечивается получение компромиссного решения, которое является наилучшим в среднем. Для получения решения, обеспечивающего наилучшие приближения для критерия, наиболее удаленного от своего оптимального значения, рассматривают обобщенный критерий
Q(x) = max 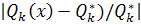 .
.
Если относительно весовых коэффициентов известно только, что они принадлежат множеству

то обобщенный критерий оптимальности можно ввести следующим образом:
Q (х) = max 
или
Q (х) = max 
Решение задачи нелинейной оптимизации с такими критериями оптимальности позволяет получить наилучшее гарантированное значение х* для наилучшего сочетания весовых коэффициентов 
Как уже отмечалось, из-за наличия внешней среды, характеризуемой довольно широким спектром внешних факторов, артиллерийские орудия как объекты для оптимального анализа и синтеза носят стохастический характер. В этом случае критерии оптимальности и ограничения являются случайными величинами, зависящими от вектора внешних факторов у:
min{Q(x, y):x 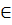 R;R = (x:gt(x, у) > 0, i=
R;R = (x:gt(x, у) > 0, i=  )}.
)}.
В нашей задаче в большинстве случаев известно лишь, что у принадлежит некоторой области Ry. Критерий оптимальности здесь назначается из условия обеспечения наилучшего результата в наихудшем по неопределенности y случае:
Q (x) = max { Q (x, у): у 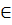 Ry; gt (x)=min (gi (x, y): y
Ry; gt (x)=min (gi (x, y): y 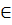 Ry;i=
Ry;i=  )}.
)}.
Таким образом, приходим к детерминированной минимаксной задаче оптимизации:
min max { Q (х, у): х 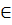 R; у
R; у 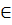 Ry;R=[x: min gt (x, у)>0,y
Ry;R=[x: min gt (x, у)>0,y 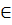 Ry;i=
Ry;i=  }.
}.
При известных законах распределения f(y) в качестве критерия оптимальности можно использовать математическое ожидание случайной функции Q(x, у):
Q(x) =M 
или квадрат стандартного отклонения значения функции от заданного
уровня
Q(x) = М | [Q (х, у) - Q+]2} = 
либо вероятность того, что случайная величина Q{x, у) превысит некоторый
заданный уровень Q-.
Q(x) = p{Q(x, у) >Q-}.
Используя эти выражения, можно в терминах математического программирования сформулировать следующие задачи стохастической оптимизации:
— найти вектор управляемых непеременных х, обеспечивающий
min  ;
;
— найти вектор управляемых переменных х, обеспечивающий
min 
где 0<p<1 — некоторая заданная вероятность выполнения системы ограничений;
— найти вектор управляемых переменных х, обеспечивающий
max  .
.
Оптимальный анализ



 ) —конструктивно-настраиваемые параметры, вектором g =
) —конструктивно-настраиваемые параметры, вектором g =  ) — параметры состояния, а вектором у=
) — параметры состояния, а вектором у=  ) —параметры среды, где п, m, l — общее число учитываемых параметров.
) —параметры среды, где п, m, l — общее число учитываемых параметров. которые минимизируют или максимизируют критерий (целевую функцию) Q (
которые минимизируют или максимизируют критерий (целевую функцию) Q (  , j = 1, п}.
, j = 1, п}. значения j-й управляемой переменной, характеризующие область ее возможных изменений.
значения j-й управляемой переменной, характеризующие область ее возможных изменений.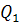 (x),...,
(x),...,  (x)) приходится при этом свертывать, конструируя с помощью приведенных ранее компромиссов скалярные функции Q(x) = f(Ql(x),..., Qn(x)).
(x)) приходится при этом свертывать, конструируя с помощью приведенных ранее компромиссов скалярные функции Q(x) = f(Ql(x),..., Qn(x)).

 такова, что в числителе стоит общая размерность, а в знаменателе — размерность соответствующего критерия
такова, что в числителе стоит общая размерность, а в знаменателе — размерность соответствующего критерия  .
. и его оптимальной величиной:
и его оптимальной величиной: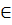 R.
R.
 . Тогда определение эффективного вектора оптимизируемых параметров сведется к решению задачи нелинейного программирования:
. Тогда определение эффективного вектора оптимизируемых параметров сведется к решению задачи нелинейного программирования:
 может быть основан на физических представлениях, предпочтении частных критериев по важности, экспертной оценке и, вообще говоря, связан с наличием определенного опыта и экспериментальной проверки.
может быть основан на физических представлениях, предпочтении частных критериев по важности, экспертной оценке и, вообще говоря, связан с наличием определенного опыта и экспериментальной проверки.
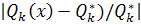 .
.



 )}.
)}.

 ;
;
 .
.


