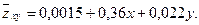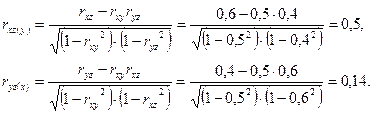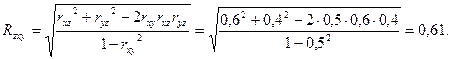Таблица 1
Используя данные, полученные в таблице 1, определим значение коэффициента корреляции по следующей зависимости:
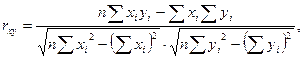
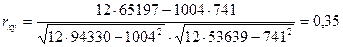
Для вывода уравнения регрессии рассчитаем математическое ожидание значений 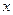 и
и 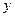 и СКО соответствующих величин:
и СКО соответствующих величин:
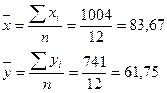

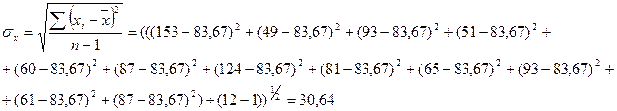
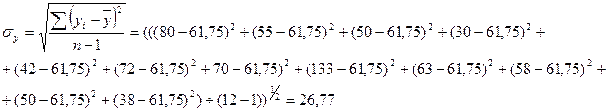
Полученные данные подставим в уравнение регрессии:
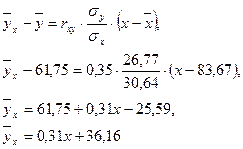
ЗАДЩАНИЕ 5
Криволинейная корреляционная связь
Если коэффициент корреляции 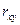 очень мал и прямолинейная связь
очень мал и прямолинейная связь 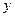 с
с 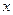 отсутствует, то возможна криволинейная связь. Для криволинейных корреляционных связей мерой силы связи является корреляционное отношение, которое определяется зависимостями:
отсутствует, то возможна криволинейная связь. Для криволинейных корреляционных связей мерой силы связи является корреляционное отношение, которое определяется зависимостями:
- для связи 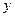 с
с 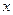
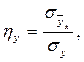
- для связи 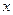 с
с 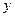
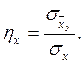
Если 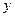 с
с 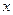 связаны однозначной связью, то
связаны однозначной связью, то 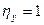 . Если связи нет, то
. Если связи нет, то 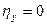 . Аналогичные свойства относятся и к
. Аналогичные свойства относятся и к 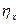 . Корреляционная связь между
. Корреляционная связь между 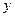 и
и 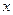 будет тем теснее, чем ближе
будет тем теснее, чем ближе 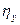 к 1, и тем слабее, чем
к 1, и тем слабее, чем 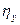 ближе к нулю.
ближе к нулю.
Наиболее часто наблюдающейся в различных технических исследованиях криволинейной корреляционной связью является параболическая связь, которая выражается параболой 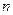 -го порядка. Рассмотрим случай, когда уравнение регрессии
-го порядка. Рассмотрим случай, когда уравнение регрессии 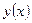 имеет вид второго порядка:
имеет вид второго порядка:
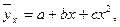
где 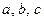 - постоянные коэффициенты,
- постоянные коэффициенты,
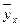 - частное среднее значение
- частное среднее значение 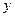 , соответствующее различным заданным значениям
, соответствующее различным заданным значениям 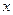 .
.
Для определения коэффициентов 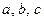 составляются три уравнения:
составляются три уравнения:
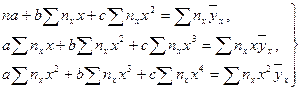 (1)
(1)
где 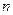 - общее число наблюдений,
- общее число наблюдений,
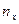 - частота каждого значения
- частота каждого значения 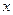 .
.
Решение этих трех уравнений дает значения коэффициентов 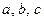 .
.
Задание. Вычислить параболическую регрессию 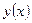 для данных, сведенных в корреляционную таблицу.
для данных, сведенных в корреляционную таблицу.
Таблица 1
Значения 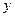
| Значения 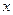
| 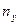
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
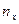
|
|
|
|
|
|
|
|
|
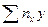
|
|
|
|
|
|
|
| -
|
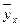
|
|
| 32,32
| 43,45
| 44,57
|
|
| -
|
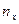
| 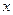
| 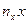
| 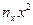
| 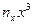
| 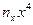
| 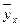
| 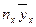
| 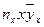
| 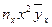
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 32,32
| 614,08
| 17194,24
| 481438,72
|
|
|
|
|
|
|
| 43,45
| 477,95
| 16250,30
| 552510,20
|
|
|
|
|
|
|
| 44,57
| 267,42
| 10696,80
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
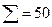
| -
|
|
|
|
| -
| 1907,45
| 56617,34
| 1771092,92
|
Подставим полученные данные в систему уравнений (1):
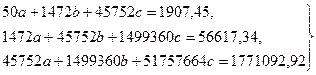
В каждом из уравнений разделим числовые коэффициенты на коэффициент при  :
:
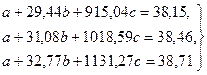
Вычтем из второго уравнения первое, а из третьего уравнения – второе:
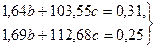
Разделим каждое из этих уравнений на соответствующий коэффициент при 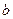 :
:

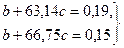
Вычтем из второго уравнения первое:
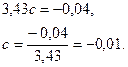
Подставим 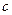 в уравнение
в уравнение 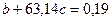 , получим:
, получим:
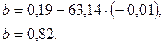
Подставим найденные значения 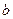 и
и 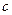 в уравнение
в уравнение 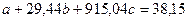 , получим:
, получим:
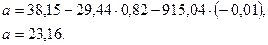
Таким образом, уравнение регрессии будет иметь вид:
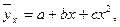
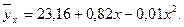
Подставив в полученное уравнение значения 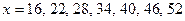 , получим теоретические значения частных средних:
, получим теоретические значения частных средних:
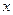
|
|
|
|
|
|
|
|
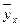
| 33,72
| 36,36
| 38,28
| 39,48
| 39,96
| 39,72
| 38,76
|
ЗАДАНИЕ 6
Множественная корреляция
Корреляционные связи могут существовать не только между двумя, но и между несколькими признаками. Например, овальность после чистового шлифования зависит от припуска на чистовое шлифование и от овальности после предварительного шлифования. Припуск на шлифование зубьев зависит от величины деформации заготовок шестерен после термической обработки и от погрешности обработки, полученной после зубонарезания.
Исследование статистических связей между многими величинами является предметом теории множественной корреляции. В практике механической обработки деталей на металлорежущих станках чаще всего встречаются случаи линейной корреляционной связи между тремя величинами или тремя факторами.
Рассмотрим простейший случай линейной корреляционной связи между тремя величинами 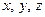 . Причем будем считать
. Причем будем считать 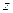 - величиной, зависящей от
- величиной, зависящей от 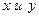 . Линейную корреляционную связь между этими величинами можно записать в виде уравнения:
. Линейную корреляционную связь между этими величинами можно записать в виде уравнения:
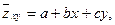
где 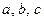 - постоянные коэффициенты, которые вычисляются с помощью коэффициентов корреляции между
- постоянные коэффициенты, которые вычисляются с помощью коэффициентов корреляции между 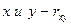 , между
, между 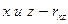 , между
, между 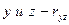 , а также СКО
, а также СКО 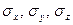 по формулам:
по формулам:
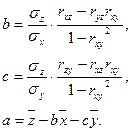
Мерой силы линейной связи между 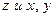 в совокупности служит коэффициент множественной корреляции или сводный коэффициент корреляции, который вычисляется следующим образом:
в совокупности служит коэффициент множественной корреляции или сводный коэффициент корреляции, который вычисляется следующим образом:
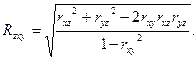
Примечание: коэффициент 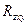 всегда положителен, его значение лежит в пределах от 0 до +1. Если
всегда положителен, его значение лежит в пределах от 0 до +1. Если 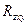 равен 0, то
равен 0, то 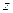 не имеет линейной связи с
не имеет линейной связи с 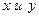 , но возможна криволинейная связь. Если
, но возможна криволинейная связь. Если 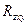 равен 1, то между
равен 1, то между 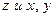 существует точно линейная связь вида
существует точно линейная связь вида 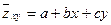 .
.
Для исследования наличия связи между 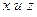 ,
, 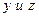 , а также для оценки влияния
, а также для оценки влияния 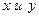 в отдельности на
в отдельности на 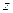 пользуются частными коэффициентами, которые обозначаются
пользуются частными коэффициентами, которые обозначаются
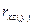 - связь между
- связь между 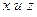 при постоянном значении
при постоянном значении 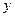 ,
,
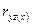 - связь между
- связь между 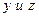 при постоянном значении
при постоянном значении 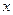 .
.
Эти коэффициенты вычисляются по формулам:
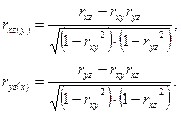
Смысл частных коэффициентов заключается в том, что они служат мерой линейной связи между 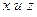 при постоянном значении
при постоянном значении 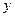 и
и 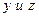 при постоянном значении
при постоянном значении 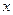 . Значения частных коэффициентов корреляции заключены в пределах от -1 до +1. Когда они равны 0, частная связь между
. Значения частных коэффициентов корреляции заключены в пределах от -1 до +1. Когда они равны 0, частная связь между 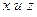 ,
, 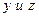 не может быть линейной. Если они равны
не может быть линейной. Если они равны 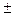 1, то связь точно линейная. Чем ближе значения частных коэффициентов к
1, то связь точно линейная. Чем ближе значения частных коэффициентов к 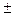 1, тем теснее связь, тем ближе она к линейной.
1, тем теснее связь, тем ближе она к линейной.
Сравнивая 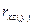 и
и 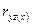 , можно установить, какой из факторов
, можно установить, какой из факторов 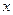 или
или 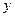 оказывает более сильное влияние на
оказывает более сильное влияние на 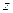 . Чем больше величина частного коэффициента корреляции, тем теснее связь данного фактора с
. Чем больше величина частного коэффициента корреляции, тем теснее связь данного фактора с 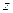 и тем сильнее его влияние на
и тем сильнее его влияние на 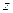 .
.
Для определения коэффициентов корреляции 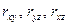 необходимо составить корреляционные таблицы для
необходимо составить корреляционные таблицы для 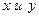 ,
, 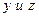 ,
, 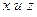 и произвести аналогичные вычисления, как было рассмотрено выше.
и произвести аналогичные вычисления, как было рассмотрено выше.
Пример. Кольца подшипников подвергаются предварительному и окончательному шлифованию на двух бесцентровых шлифовальных станках. Статистическими исследованиями установлено, что овальность после предварительного шлифования - 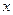 , припуск под окончательное шлифование -
, припуск под окончательное шлифование - 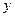 , овальность после окончательного шлифования -
, овальность после окончательного шлифования - 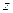 характеризуются следующими показателями:
характеризуются следующими показателями:
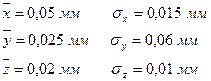
Установлены следующие величины коэффициентов корреляции между 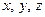 :
:
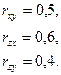
Необходимо определить:
- коэффициент множественной корреляции 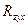 ;
;
- уравнение регрессии 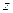 по
по 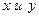 ;
;
- частные коэффициенты корреляции 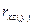 и
и 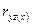 .
.
Вычислим значения коэффициентов 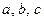 :
:
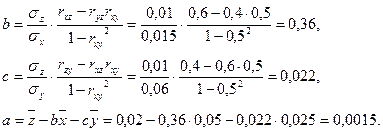
Уравнение корреляционной связи 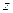 с
с 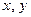 :
:
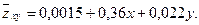
Вычислим частные коэффициенты корреляции:
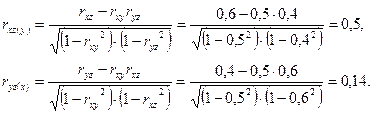
Коэффициент множественной корреляции
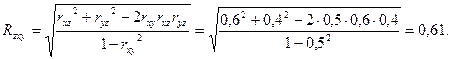
Этот коэффициент достаточно велик и свидетельствует о наличии линейной связи между 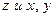 .
.
Частные коэффициенты корреляции показывают, что влияние 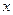 на
на 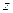 сильнее влияния
сильнее влияния 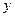 на
на 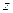 , так как связь между
, так как связь между 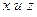 теснее, чем связь между
теснее, чем связь между 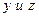 . То же вытекает из анализа уравнения регрессии
. То же вытекает из анализа уравнения регрессии 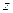 по
по 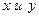 . Следовательно, влияние овальности колец после предварительного шлифования сильнее, чем влияние припуска под чистовое шлифование на величину овальности после окончательной обработки.
. Следовательно, влияние овальности колец после предварительного шлифования сильнее, чем влияние припуска под чистовое шлифование на величину овальности после окончательной обработки.
ЗАДАНИЕ 7



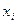
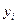
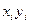
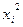
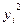
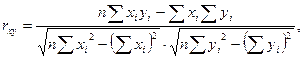
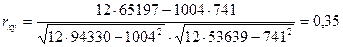
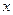 и
и 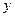 и СКО соответствующих величин:
и СКО соответствующих величин: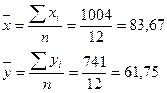

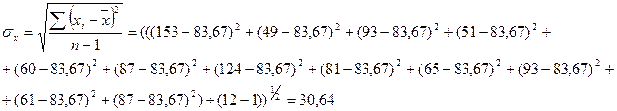
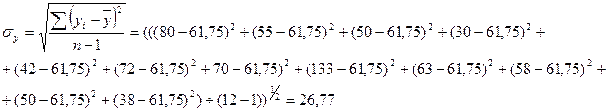
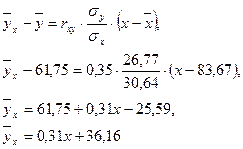
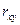 очень мал и прямолинейная связь
очень мал и прямолинейная связь 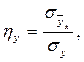

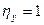 . Если связи нет, то
. Если связи нет, то 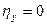 . Аналогичные свойства относятся и к
. Аналогичные свойства относятся и к 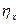 . Корреляционная связь между
. Корреляционная связь между 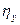 к 1, и тем слабее, чем
к 1, и тем слабее, чем 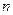 -го порядка. Рассмотрим случай, когда уравнение регрессии
-го порядка. Рассмотрим случай, когда уравнение регрессии 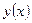 имеет вид второго порядка:
имеет вид второго порядка: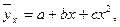
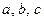 - постоянные коэффициенты,
- постоянные коэффициенты,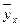 - частное среднее значение
- частное среднее значение 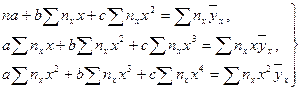 (1)
(1)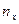 - частота каждого значения
- частота каждого значения 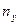
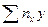
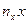
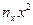
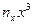
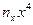
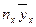
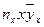
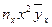
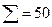
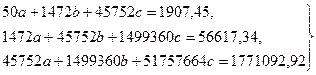
 :
: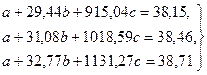
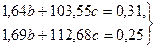
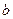 :
: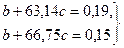
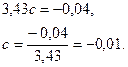
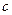 в уравнение
в уравнение 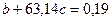 , получим:
, получим: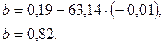
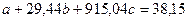 , получим:
, получим: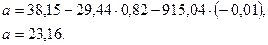
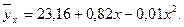
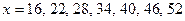 , получим теоретические значения частных средних:
, получим теоретические значения частных средних:
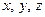 . Причем будем считать
. Причем будем считать 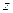 - величиной, зависящей от
- величиной, зависящей от 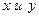 . Линейную корреляционную связь между этими величинами можно записать в виде уравнения:
. Линейную корреляционную связь между этими величинами можно записать в виде уравнения: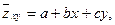
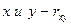 , между
, между 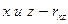 , между
, между 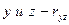 , а также СКО
, а также СКО 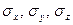 по формулам:
по формулам: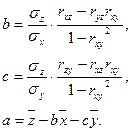
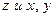 в совокупности служит коэффициент множественной корреляции или сводный коэффициент корреляции, который вычисляется следующим образом:
в совокупности служит коэффициент множественной корреляции или сводный коэффициент корреляции, который вычисляется следующим образом: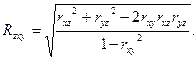
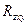 всегда положителен, его значение лежит в пределах от 0 до +1. Если
всегда положителен, его значение лежит в пределах от 0 до +1. Если 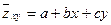 .
.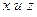 ,
, 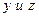 , а также для оценки влияния
, а также для оценки влияния 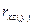 - связь между
- связь между 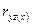 - связь между
- связь между 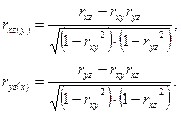
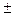 1, то связь точно линейная. Чем ближе значения частных коэффициентов к
1, то связь точно линейная. Чем ближе значения частных коэффициентов к 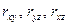 необходимо составить корреляционные таблицы для
необходимо составить корреляционные таблицы для 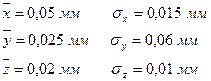
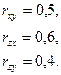
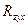 ;
;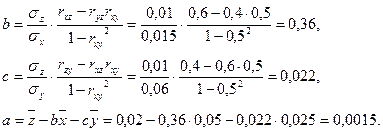
 :
: