Эмпирические формулы – это приближенные значения аналитических формул или формулы, описывающие закономерности результатов эксперимента.
На основании экспериментальных данных можно подобрать алгебраическое выражение функции
 ,
,
которое называется эмпирической формулой в пределах измеренных значений аргументов х 1… хn.
Замену точных выражении приближенными, более простыми называют аппроксимацией, а сами функции – аппроксимирующими. Они имеют ограниченную область применения, которая не должна выходить за пределы опытных данных, т.е. по ним надёжно можно проводить только интерполяцию, но не экстраполяцию.
Процесс подбора эмпирических формул состоит из следующих этапов.
1) Данные измерений наносят на сетку прямоугольных координат; по экспериментальным точкам проводят плавную кривую и выбирают ориентировочно вид формулы.
2) Вычисляют параметры формулы, которые наилучшим образом соответствовали бы принятой формуле и результатам измерений.
Подбор необходимо начинать с уравнения прямой линии
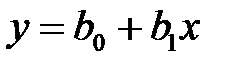 ,
,
где b 0, b 1 – постоянные коэффициенты.
Оно представляет собой простое выражение. Поэтому при анализе графического материала необходимо по возможности использовать линейную функцию. Если в равномерных координатах экспериментальные данные ложатся в виде кривой, то применяют метод выравнивания, т.е. кривую представляют в виде линейной функции
 ,
,
где  ;
;  , т.е. новые оси координат имеют не равномерную, а функциональную сетку.
, т.е. новые оси координат имеют не равномерную, а функциональную сетку.
Далее строят прямую в координатах «X - Y», по которой вычисляют параметры b 0, b 1 (рис.14).
 (или Yi при X = 0)
(или Yi при X = 0)
 .
.



Рис.14. Выравнивание нелинейной зависимости
с помощью функциональных осей координат
Прямую целесообразно проводить, используя метод наименьших квадратов, т.е. для лучшей прямой сумма квадратов отклонений εi от прямой должна быть наименьшей
 .
.
Для облегчения и упрощения расчётов часто используется метод нулевых средних, когда
 .
.
Когда экспериментальная кривая на равномерной сетке прямоугольных координат имеет плавный вид, целесообразно использовать графический метод выравнивания.
Рассмотрим некоторые характерные кривые, их функциональные зависимости и способы выравнивания. На рис.15 представлены 4 вида кривых. Кривые вида 1 могут быть аппроксимированы зависимостью
 .
.
Логарифмируя правую и левую часть, получаем
 .
.
Или в новой системе координат
 ,
,
где  ,
,  , т.е. на двойной логарифмической сетке будет прямая линия, у которой
, т.е. на двойной логарифмической сетке будет прямая линия, у которой
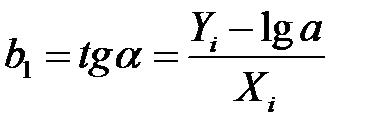 .
.

Рис.15. Характерные кривые для графического выравнивания
Однако графическое выравнивание (спрямление) с помощью логарифмических сеток можно использовать, когда значение аргумента X > 0 и X ≠ 1.
Пример: В результате эксперимента получены следующие данные
| x
|
|
|
|
|
|
|
|
|
| yэ
| 1,06
| 1,36
| 1,51
| 1,71
| 1,78
| 1,92
| 2,00
| 2,11
|
| y
| 1,06
| 1,33
| 1,52
| 1,68
| 1,81
| 1,92
| 2,02
| 2,11
|
где yэ – экспериментальные значения;
y – расчётные значения по зависимости
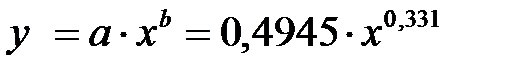 .
.
Приведённая зависимость получена следующим образом. На график в равномерной системе координат «х-у» наносятся экспериментальные точки «х-уэ». Проводят визуальную графическую обработку и определяют значение двух крайних точек у. Для нахождения параметров а и b составляют и решают систему уравнений
 или
или  ,
,
откуда b = 0,331, а = 0,4945.
Кривая 2 может быть аппроксимирована зависимостью
 .
.
После логарифмирования получаем
 ,
,
или  ,
,
т.е. спрямление реализуется в полулогарифмической системе координат (логарифмическая сетка по оси Y и равномерная – по х).
Пример:
| x
| 1,0
| 1,5
| 2,0
| 2,5
| 3,0
| 3,5
| 4,0
| 4,5
|
| yэ
| 15,2
| 20,8
| 27,2
| 36,8
| 49,0
| 66,3
| 87,1
| 117,5
|
| y
| 15,20
| 20,36
| 27,27
| 36,52
| 48,91
| 65,51
| 87,74
| 117,5
|
Система уравнений по двум крайним точкам, полученным после графической обработки экспериментальных данных.
 или
или  ,
,
т.е. b = 0,5843, а = 8,475,  .
.
Кривые типа 3 аппроксимируются зависимостью
 .
.
Замена  даёт прямую линию на сетке прямоугольных координат (y-X)
даёт прямую линию на сетке прямоугольных координат (y-X)
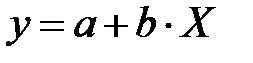 .
.
Кривые типа 4 аппроксимируются зависимостью
 .
.
Изменяя сетку по оси «у» на 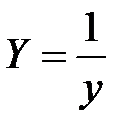 , получаем прямую линию в системе координат «х-У», т.е. по оси х сетка не изменяется
, получаем прямую линию в системе координат «х-У», т.е. по оси х сетка не изменяется
 .
.
При подборе эмпирических формул широко используется полином типа
 ,
,
где b 0, b 1, b 2... bn – постоянные коэффициенты.
Полиномами можно аппроксимировать любые результаты измерений, если они графически выражаются непрерывными функциями.
Для определения коэффициентов «b», кроме графического метода, применяют также метод средних отклонений и метод наименьших квадратов. Рассмотрим более подробно эти методы.
13.3. Метод средних отклонений
Метод средних отклонений основан на следующем положении. По экспериментальным данным (точкам) можно построить множество плавных, кривых. Наилучшей будет та кривая, у которой сумма разностных отклонений будет равна нулю, т.е.
 .
.
Порядок расчёта коэффициентов полинома состоит в следующем.
Экспериментальные данные изменения «у» от «х» заносят в таблицу, строится диагональная таблица тех разностей, которые можно принять постоянными. Например, для семи экспериментальных точек диагональная таблица разностей имеет следующий вид.
Определяется число ряда и степень полинома «n». Обычно берётся n = 3...4. В принятый полином последовательно подставляются координаты х и у нескольких экспериментальных точек (m). Получают систему из «m» уравнений, линейных относительно неизвестных коэффициентов «b». Каждое уравнение приравнивается соответствующему отклонению ε, которое представляет собой разность между экспериментальным и расчётным значением «у» (рис. 16). Число точек «m» должно быть больше степени полинома «n», т.к. иначе система уравнений не решается. Если m значительно больше n, то сначала разбивают все уравнения на n +1 группы по мере увеличения переменной х. В каждой группе складывают уравнения и получают новую систему уравнений, равную n +1 групп.
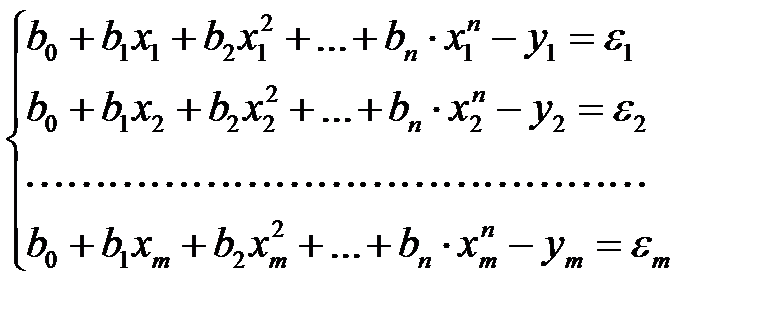 .
.
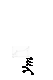





 0 0
|
Рис.16. Экспериментальные точки и аппроксимирующая кривая
Решая систему линейных уравнений, определяют коэффициенты «b» аппроксимирующего полинома. Метод средних обладает высокой точностью при большом числе точек (m > 4).
Пример
Таблица 6
| x
|
|
|
|
|
|
|
|
| yэ
| 8,8
| 6,5
| 4,8
| 3,6
| 2,7
| 2,1
| 1,7
|

|
| 2,3
| 1,7
| 1,2
| 0,9
| 0,6
| 0,4
|
|

|
| 0,6
| 0,5
| 0,3
| 0,3
| 0,2
|
|
|
| 0,1
| 0,2
|
| 0,1
|
|
| y
| 8,71
| 6,6
| 4,87
| 3,54
| 2,59
| 2,04
| 1,88
|
| | | | | | | | | | | | | | | |
Выбираем полином второй степени
 .
.
Разбиваем систему из 7 уравнений на 3 группы, считая, что внутри групп также действует принцип
 ,
,
где к - количество уравнений в группе.
Тогда, суммируя уравнения в каждой группе, получаем систему из 3-х уравнений с 3-я неизвестными коэффициентами b 0, b 1, b 2.

| 
| – 1-я группа,
– 2-я группа,
– 3-я группа.
|
 или или
|

|
Решая уравнения относительно коэффициентов b 0, b 1, b 2 и подставляя их значения в выбранный полином, получаем
 .
.
Результаты расчета значений «y» по аппроксимирующему полиному приведены в таблице 6.
Метод средних может также быть применён для различных кривых после их выравнивания (спрямления).
Пример
Таблица 7
| x
|
|
|
|
|
|
|
|
|
| yэ
| 57,6
| 41,9
| 31,0
| 22,7
| 16,6
| 12,2
| 8,9
| 6,5
|
| y
| 57,29
| 42,01
| 30,81
| 22,59
| 16,5
| 12,15
| 8,91
| 6,53
|
Анализ представленной в виде таблицы зависимости в прямоугольной системе координат дает возможность аппроксимировать ее зависимостью
 ,
,
или

 ,
,
где  ,
, 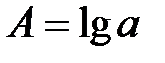 ,
, 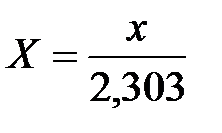
Так как необходимо определить только 2 параметра (А, b), то все результаты измерений делим на 2 группы:
| I-я группа
|
| II-я группа
|
1.  ; ;
|
| 5.  ; ;
|
2.  ; ;
|
| 6.  ; ;
|
3.  ; ;
|
| 7.  ; ;
|
4. 
|
| 8. 
|
|
|
|
|

|
| 
|
Решая систему из двух уравнений, получаем  ,
, 
 , тогда
, тогда  .
.
Расчетные значения y приведены в табл.7.
Метод наименьших квадратов
Метод нулевых средних отклонений не даёт единственного решения, т.к. его результаты зависят от способа группирования экспериментальных данных. Это вызывает некоторую неопределённость. Указанного недостатка лишён метод наименьших квадратов. Суть его заключается в том, что если все измерения функции  проведены с одинаковой точностью и ошибки измерений распределяются по нормальному закону, то параметры выбранного аппроксимирующего уравнения однозначно определяются из условия.
проведены с одинаковой точностью и ошибки измерений распределяются по нормальному закону, то параметры выбранного аппроксимирующего уравнения однозначно определяются из условия.
 ,
,
т.е. сумма квадратов отклонении измеряемых значении от расчетных принимает наименьшее значение.
При этом получается только одно решение (формула) – лучшая из всех возможных.
Некоторый недостаток метода наименьших квадратов состоит в том, что он трудоёмок при большом числе начальных уравнений.
Рассмотрим сущность метода наименьших квадратов на примере, когда
экспериментальные данные аппроксимируются полиномом 3-й степени  , а их количество m >> 4. Тогда для каждой точки
, а их количество m >> 4. Тогда для каждой точки
 ,
,  ,
,
где yi – значение функции для аргумента xi, рассчитанное по аппроксимирующему полиному;
yiэ – экспериментальное значение функции при аргументе xi;
εi – отклонение экспериментального (измеренного) значения функции от расчетного при аргументе xi.
Подставив экспериментальные значения хiэ и уiэ в выбранное уравнение и возведя в квадрат правые и левые части, получаем
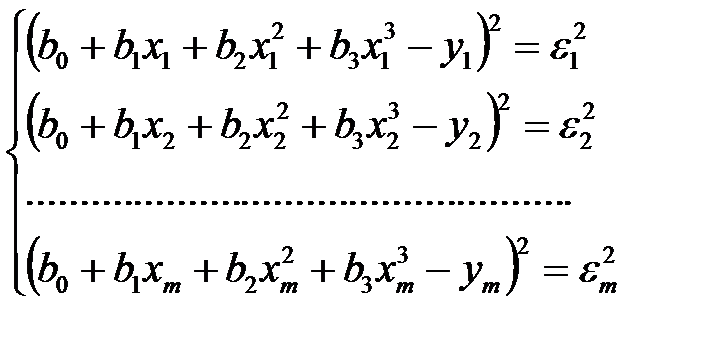 .
.
Просуммируем левые и правые части приведённой выше системы уравнений

Если переменными величинами считать коэффициенты b0, b1, b2, b3, то условие минимума приведённого выражения  будет
будет
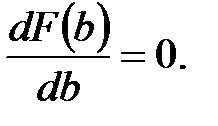
Возьмём частные производные по b0, b1, b2, b3
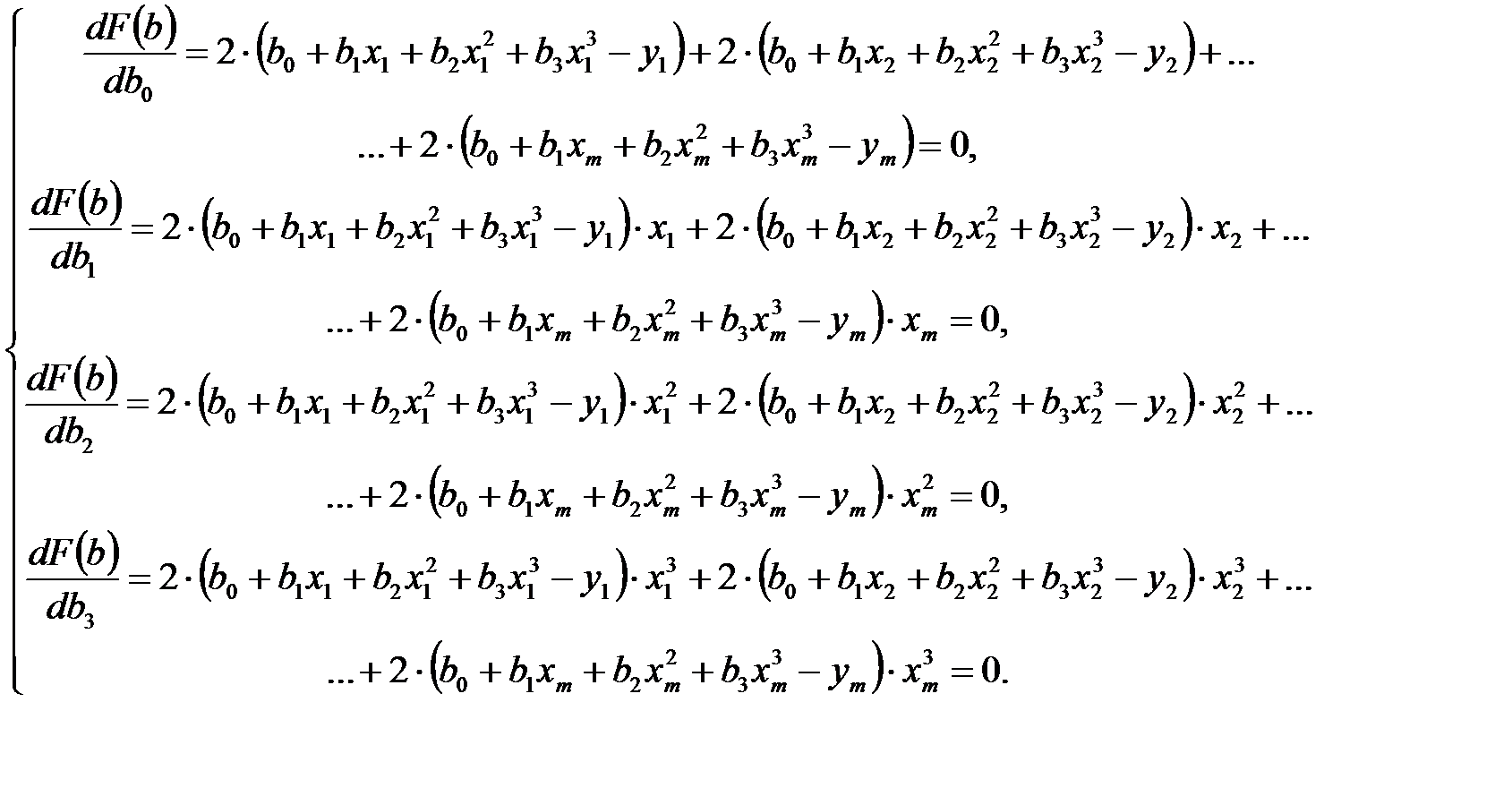
Последние уравнения называются нормальными. Их можно записать по-другому. Для этого раскроем скобки каждого уравнения и просуммируем слагаемые с одинаковыми коэффициентами. После преобразований получаем

Таким образом, имеется 4 нормальных уравнения для нахождения 4-х неизвестных коэффициентов, т.е. по отношению к коэффициентам «b» имеем систему линейных уравнений. Для полинома 2-й степени система нормальных уравнений имеет следующий вид.

Соответственно для прямой линии имеем 2 уравнения с 2-мя неизвестными b 0, b 1.
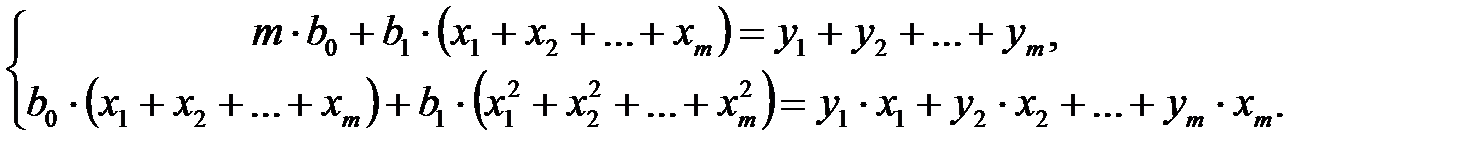
Пример
m = 6, n = 1
Таблица 8
| №
|
|
|
|
|
|
|
| x
| 0,5
| 1,0
| 1,5
| 2,0
| 2,5
| 3,0
|
| y
| 0,62
| 1,64
| 2,58
| 3,70
| 5,02
| 6,04
|
Графическая обработка экспериментальных данных показала, что они могут быть аппроксимированы прямой линией  . Составим нормальные уравнения.
. Составим нормальные уравнения.

Тогда

Решаем эту систему относительно b 0, b 1, получим b 0 = –0,57, b 1 = 2,192, т.е.

Обработка результатов эксперимента по методу средних отклонений даёт уравнение прямой следующего вида:

Если результаты эксперимента аппроксимировать параболой 2-й степени, то её уравнение будет

ПЛАНИРОВАНИЕ И ОБРАБОТКА РЕЗУЛЬТАТОВ МНОГОФАКТОРНОГО ЭКСПЕРИМЕНТА
14.1. Общие положения и основные понятия.
При проведении экспериментальных исследований отдельно и совместно могут решаться две задачи:
1) экстремальная,
2) интерполяционная (задача описания)
Экстремальная задача заключается в отыскании условий процесса, обеспечивающих получение оптимальных значений выбранного критерия (например, стойкости инструмента, шероховатости, производительности и др.) Интерполяционная задача состоит в построении интерполяционной формулы для предсказания (прогнозирования) значения изучаемого параметра, зависящего от ряда факторов.
Для решения указанных задач необходимо построение модели изучаемого процесса на основе выполненных экспериментальных исследований.
При этом необходимо спланировать эксперимент так, чтобы получить максимум информации по минимальному числу опытов. Этого можно достичь путём математического планирования эксперимента, т.е. путём использования комбинаторных методов, при которых одновременно варьируется несколько входных параметров (факторов). Под планированием эксперимента понимается процедура выбора числа и условий проведения опытов, необходимых для решения поставленной задачи с требуемой точностью. Математическое планирование эксперимента позволяет:
1) свести число опытов к минимуму,
2) выбрать эффективные процедуры выполнения экспериментов,
3) пользоваться математическим аппаратом,
4) одновременно варьировать всеми переменными,
5) оценивать погрешности результатов опытов.
Другими словами, задача планирования экспериментов заключается в установлении минимально необходимого количества опытов, условий их проведения, в выборе методов математической обработки результатов опытов, в принятии решений. При этом должен быть четко сформулирован критерий оценки результатов исследований, заданный количественно. Его называют откликом, зависимой переменной, параметром оптимизации или функцией цели.
Процессы, изучаемые в технологии машиностроения, отличаются большой сложностью и трудно поддаются описанию корректными детерминированными математическими моделями. Поэтому широко применяется эмпирический подход к построению математических моделей. В этом случае исследуемый процесс представляется в виде «черного ящика», под которым понимаются системы и структуры, внутренние процессы в которых неизвестны или очень сложны. Методы изучения таких систем основаны на исследовании их реакции на заданные входные сигналы. При исследовании сложных объектов и процессов на начальном этапе или для практических целей целесообразнее не выявлять их внутреннее устройство и физические особенности (закономерности), а воздействовать на них таким образом, чтобы можно было надёжно получать и изменять выходные параметры. Зная входные и выходные параметры, можно между ними установить функциональную связь, на основе которой можно прогнозировать свойства объекта или процесса, проводить их оптимизацию и управлять ими. Схематически модель «чёрного ящика» представлена на рис. 17.
Факторы х 1, х 2, х 3,..., хк называют основными, факторы ω 1, ω 2, ω 3, …, ωm, – случайными. Операторы А 1(...), А 2(...), А 3(...), …, Аl (...) характеризуют взаимосвязь входных и выходных параметров.
Для упрощения решения поставленной задачи число основных факторов стараются сократить до минимума, относя к случайным даже хорошо изученные, но слабо влияющие на выходные параметры факторы.
Методика «чёрного ящика» более всего применима для проведения экстремальных экспериментов.
| A 1(…)
A 2(…)
A 3(…)
…
Al (…)
|
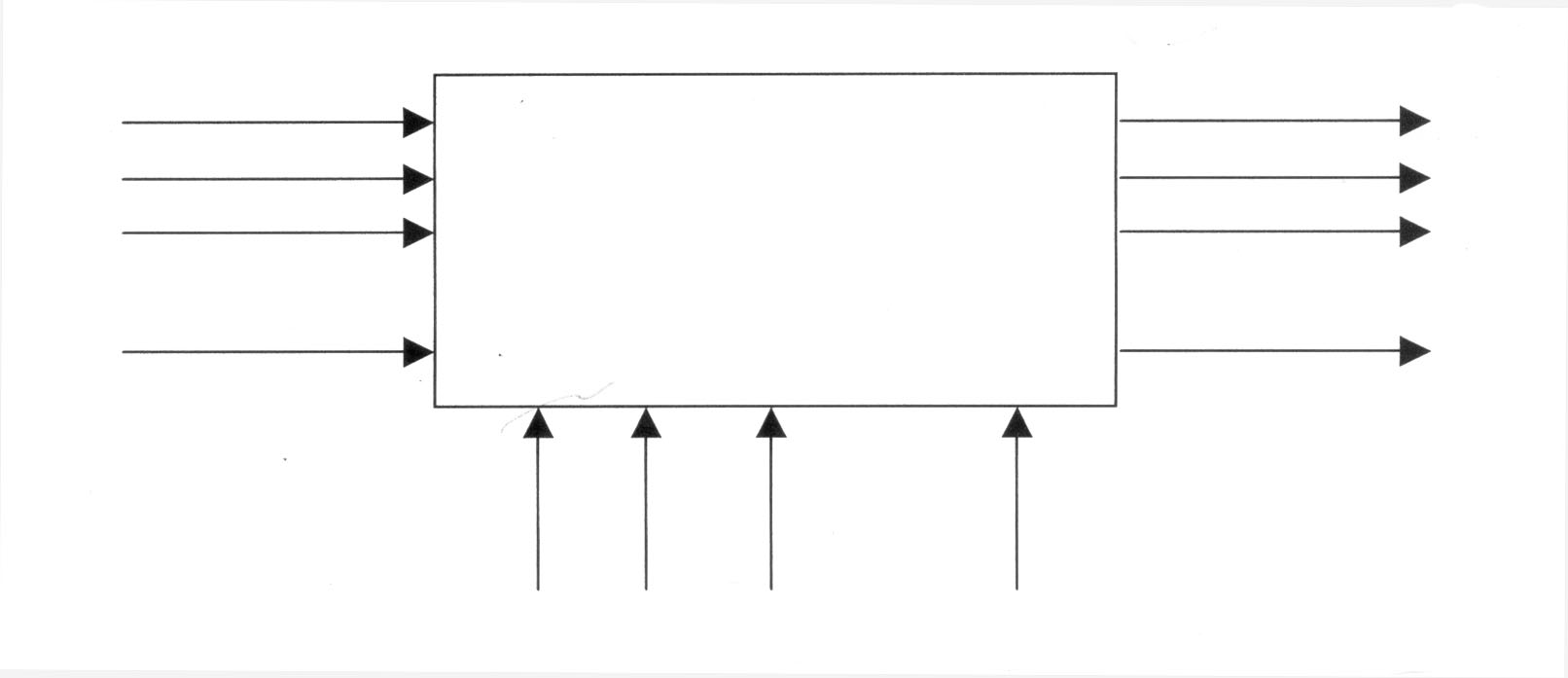
Рис.17. Модель «черного ящика»:
x 1, x 2, x 3, …, xn – входные основные факторы;
y 1, y 2, y 3, …, yn – выходные параметры;
ω 1, ω 2, ω 3, …, ωm – неконтролируемые факторы (шумы);
А 1(...), А 2(...), А 3(...), …, Аl (...) – операторы.
Предполагается, что между входом и выходом существует определённая связь. Задача сводится к постановке минимального числа экспериментов (вариантов уровней входных параметров), регистрации значений выходных параметров, построению и анализу математических моделей, связывающих входные и выходные параметры. При этом сложность задачи состоит в том, что нужно получить функции отклика, вид которых исследователю в большинстве случаев неизвестен. Так как исследователь имеет дело с выборочными оценками выходных параметров уi, то приближённое уравнение функции отклика строится в виде
 , где i = 1, 2, 3,… n.
, где i = 1, 2, 3,… n.
Это уравнение в многомерном факторном пространстве отражается поверхностью отклика.
При разработке эмпирических математических моделей не исходят из физических законов и соотношений. Они должны отвечать одному условию –заданной точности вычислений выходных параметров, т.е. обеспечивать совпадение расчётных и экспериментальных их значений в установленных пределах.
В этом случае говорят, что математическая модель адекватна, т.е. пригодна для описания изучаемого процесса или объекта. Погрешность адекватности – это погрешность в описании данного явления, возникающая вследствие недостаточного соответствия аппроксимирующей функции экспериментальным данным. Для достижения большей адекватности модель шаг за шагом усложняют. Останавливаются на модели, которая ещё относительно проста, но погрешность адекватности – приемлема.
Сегодня нет общего метода нахождения эмпирических формул лучшего вида для любых экспериментальных данных. Наибольшее применение нашли модели в виде алгебраических полиномов, хотя не для всякой аппроксимации они являются лучшими. При этом исходят из того, что неизвестную функцию отклика в некоторой области факторного пространства можно разложить в степенной бесконечный ряд Тейлора.

Аппроксимация в виде алгебраического полинома обоснована, если исследуемая зависимость отвечает требованию непрерывности и «гладкости». Так как заранее это неизвестно, то делается допущение, что это так.
Модель, построенная на основании ограниченного числа экспериментов, будет несколько отличаться своими коэффициентами от теоретически возможной модели.

Это уравнение называют уравнением регрессии, a b0, bi, bij, bii –коэффициенты модели, подлежащие определению.
При этом количество коэффициентов математической модели не должно быть больше числа степеней свободы, под которым в статистике понимается разность между числом статистических данных и числом наложенных связей. Применительно к уравнению регрессии число степеней свободы – это разность между количеством опытов и количеством коэффициентов матмодели, вычисленных по результатам этих опытов независимо друг от друга. Для линейной модели число степеней свободы определяется по формуле
 ,
,
где k – число факторов (коэффициентов),
N – число опытов,
f – число степеней свободы.
На первом этапе планирования экстремальных экспериментов, чтобы определить направление движения к оптимуму функции «у», достаточно описать величину «у» полиномом 1-ой степени (линейной моделью)

Для линейной модели эксперименты проводят по плану, называемому планом 1-го порядка или линейным.
В области оптимума функцию отклика пытаются описать линейной моделью, неполной квадратичной моделью типа

либо полиномом 2-ой степени

При построении модели последнего вида эксперименты проводят по плану, называемому планом 2-го порядка.
Степенные зависимости, которые часто используются в технологии
машиностроения и особенно в теории резания материалов, могут быть
приведены к полиномной форме логарифмированием. |
Пример
 ;
;  ,
,
или  ,
,
где y = ln V; b 0 = CV; b 1 = XV; b 2 = YV; b 3 = m; x 1 = ln t; x 2 = ln S; x 3 = ln T.
В интерполяционных задачах функцию отклика вначале описывают линейной моделью и проверяют ее адекватность. Если модель адекватна, то исследование заканчивают. В противном случае модель постепенно усложняют, проверяя на каждом этапе её адекватность.
При исследовании многофакторного процесса получение математической модели связано со значительными трудностями, т.к. число всех возможных опытов велико.
Для облегчения решения этой задачи наиболее целесообразно использование статистических методов планирования экспериментов, которые позволяют установить минимальное количество опытов, необходимое и достаточное для решения поставленной задачи с требующей точностью.
Процедура планирования экспериментов состоит из следующих этапов:
1) выбора параметра оптимизации (для экстремальных экспериментов),
2) выбора математической модели (уравнения регрессии),
3) выбора независимых переменных факторов и интервалов их варьирования,
4) построения плана эксперимента,
5) реализации плана эксперимента,
6) определения коэффициентов уравнения регрессии,
7) оценки статистической значимости коэффициентов уравнения регрессии и адекватности полученной математической модели.
Важным этапом процедуры планирования экстремальных экспериментов является выбор параметра оптимизации. К нему предъявляется ряд требований:
- наличие физического или экономического смысла,
- возможность количественной оценки,
- доступность для измерений,
- однозначность,
- эффективность,
- значимость для всех состояний исследуемого объекта или процесса.
Однозначность (в статистическом смысле) означает, что заданному состоянию уровней факторов должно соответствовать одно (в пределах ошибки эксперимента) значение параметра оптимизации.
Эффективность означает, что параметр оптимизации должен определяться с максимальной точностью. Это позволяет сократить до минимума число параллельных опытов. Нахождение оптимума возможно, если выбран один параметр оптимизации, а другие выступают в качестве ограничений.
Пример.
На операции токарной обработки необходимо обеспечить минимальную себестоимость операции при заданной стойкости режущего инструмента и производительности. Основным параметром оптимизации является минимальная себестоимость, а в качестве ограничивающих параметров приняты стойкость инструмента и производительность. Необходимо иметь минимальное количество параметров оптимизации (лучше 1), для чего разработано много способов их уменьшения. Один из них заключается в определении корреляционной связи (коэффициентов корреляции) между каждыми двумя параметрами. При наличии сильной корреляции любой из них может быть исключён из рассмотрения. Исключать лучше те параметры, которые трудно определять экспериментально или физический смысл которых менее ясен.
На следующем этапе предпланирования экспериментов определяется состав варьируемых факторов и устанавливается область их определения.
Фактор – это управляемая независимая переменная, соответствующая одному из возможных способов воздействия на объект исследования. Область определения фактора – это совокупность всех значений, которое может принимать фактор. Она ограничивается техническими, экономическими или другими соображениями. Например, частота вращения шпинделя и величина подачи ограничены возможностями станка.
К факторам предъявляются следующие требования:
1) управляемость, т.е. возможность поддержания на заданном уровне в течение всего опыта;
2) однозначность и непосредственное воздействие на изучаемый объект;
3) совместимость факторов (все их комбинации должны быть осуществимы и безопасны);
4) независимость, т.е. возможность установления уровня данного фактора независимо от уровня других факторов.
При экспериментальных исследованиях необходимо учитывать все существенные факторы. При большом числе факторов проводят отсеивающие эксперименты или априорное ранжирование факторов.
Затем для каждого фактора устанавливаются основные (нулевые) уровни и определяются границы изменения (интервалы варьирования), т.е. определяется область эксперимента. Следует иметь в виду, что выбор факторов и области эксперимента – задача не формализованная, она требует творческого участия экспериментатора.
Основным уровнем факторов называют их значение, принятое за исходное в плане эксперимента. Его стремятся выбрать таким образом, чтобы принятому значению факторов соответствовало минимальное или максимальное значение функции отклика, известное из априорной информации. Интервал варьирования – это разность между основным и верхним или нижним уровнями факторов. Он не может быть меньше ошибки экспериментального фиксирования уровня фактора, а также не может быть настолько большим, чтобы верхний или нижний уровни выходили за пределы области определения факторов. Увеличение интервалов варьирования затрудняет возможность линейной аппроксимац



 ,
,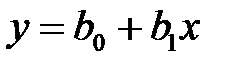 ,
, ,
, ;
;  , т.е. новые оси координат имеют не равномерную, а функциональную сетку.
, т.е. новые оси координат имеют не равномерную, а функциональную сетку. (или Yi при X = 0)
(или Yi при X = 0) .
.


 .
. .
. .
. .
. ,
, ,
,  , т.е. на двойной логарифмической сетке будет прямая линия, у которой
, т.е. на двойной логарифмической сетке будет прямая линия, у которой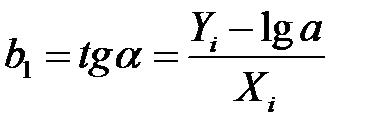 .
.

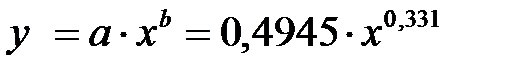 .
. или
или  ,
, .
. ,
, ,
, или
или  ,
, .
. .
. даёт прямую линию на сетке прямоугольных координат (y-X)
даёт прямую линию на сетке прямоугольных координат (y-X)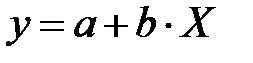 .
. .
.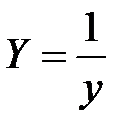 , получаем прямую линию в системе координат «х-У», т.е. по оси х сетка не изменяется
, получаем прямую линию в системе координат «х-У», т.е. по оси х сетка не изменяется .
. ,
, .
.

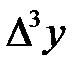



























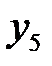









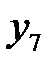
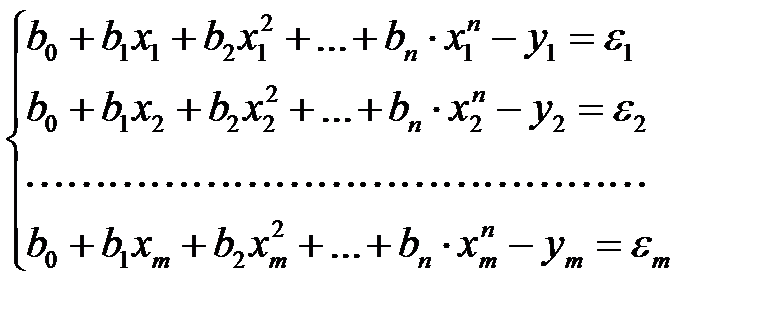 .
.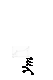





 .
. ,
,

 или
или

 .
. ,
,
 ,
, ,
, 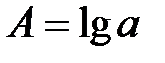 ,
, 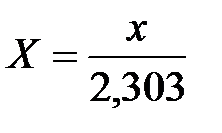
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;




 ,
, 
 , тогда
, тогда  .
. проведены с одинаковой точностью и ошибки измерений распределяются по нормальному закону, то параметры выбранного аппроксимирующего уравнения однозначно определяются из условия.
проведены с одинаковой точностью и ошибки измерений распределяются по нормальному закону, то параметры выбранного аппроксимирующего уравнения однозначно определяются из условия. ,
, , а их количество m >> 4. Тогда для каждой точки
, а их количество m >> 4. Тогда для каждой точки ,
,  ,
,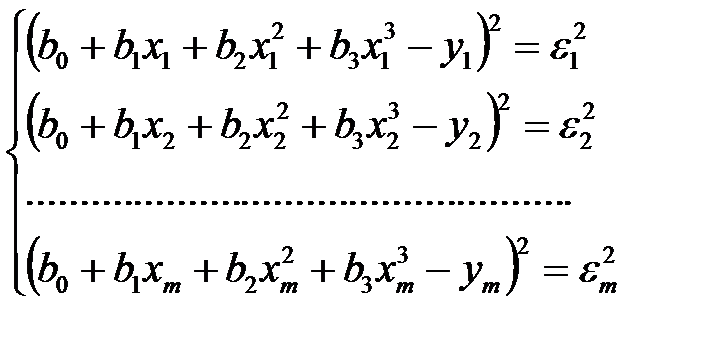 .
.
 будет
будет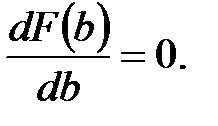
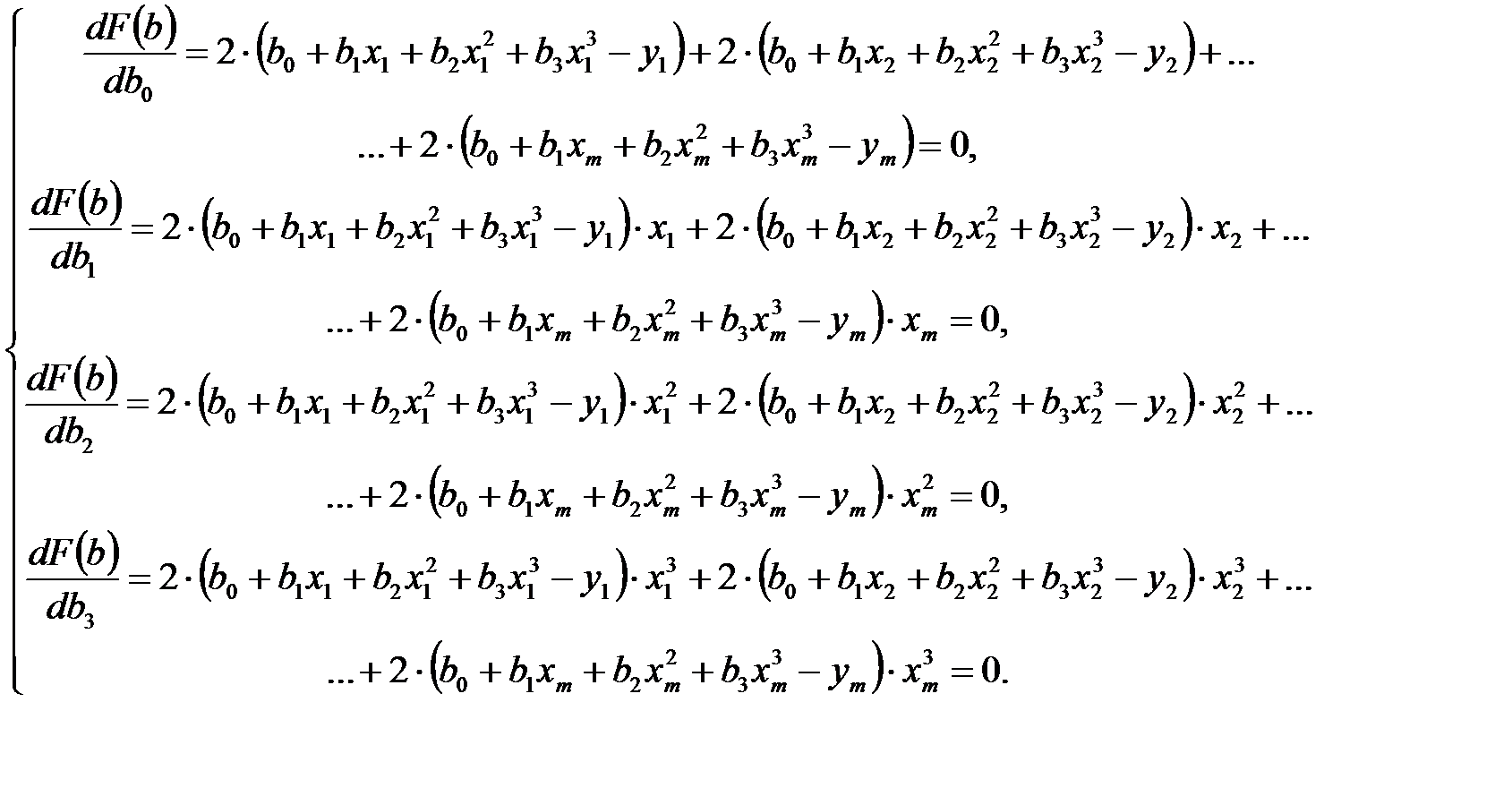


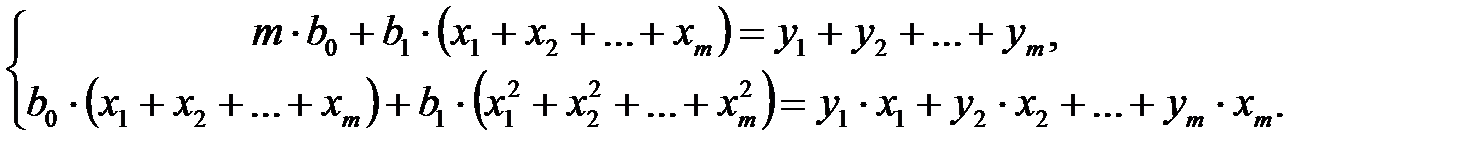
 . Составим нормальные уравнения.
. Составим нормальные уравнения.





 , где i = 1, 2, 3,… n.
, где i = 1, 2, 3,… n.

 ,
,


 ;
;  ,
, ,
,


