ЛЕКЦИЯ 1
- СИЛЫ И ДЕЙСТВИЯ НАД НИМИ
Теоретическая механика представляет собой науку об общих законах механического движения и механического взаимодействия материальных тел. В теоретической механике изучается одна из форм движения материи – механическое движение, состоящее в том, что тело с течением времени изменяет своё положение в пространстве по отношению к другим телам. Механическим называют тот вид взаимодействия тел, в результате которого происходит изменение их движения или изменение их формы (деформация).
В механике рассматриваются различные модели материальных тел: материальная точка, механическая система, сплошное тело и т.д. В первом разделе теоретической механики – статике в основном используется модель абсолютно твёрдого тела, в которой пренебрегают малыми изменениями формы тела (деформациями).
Абсолютно твёрдым называется тело, в котором расстояние между любыми двумя точками не изменяется при любых механических взаимодействиях.
Изменение состояния тела – нарушение состояния покоя или изменение характера движения происходят в результате его механического взаимодействия с другими телами.
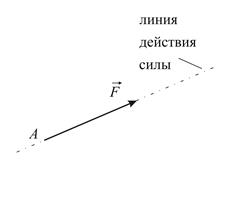
Фундаментальным понятием механики является сила, которая представляет собой количественную меру механического взаимодействия материальных тел. Сила – величина векторная. Её действие на тело определяется численным значением или модулем силы, направлением действия и точкой приложения (Рис.1.1). Прямая, вдоль которой направлена сила, называется линией действия силы. Единицей измерения силы в системе СИ является ньютон (Н).
|
| 
|
| Рис.1.1
|
| Рис.1.2
|
Характер механического взаимодействия материальных тел определяет третий закон Ньютона (Рис. 1.2):
Два материальных тела взаимодействуют с силами, равными по модулю и
Действующими по одной прямой в противоположные стороны.
Различают свободные и несвободные тела. Перемещения в пространстве несвободного тела ограничены. Тело, ограничивающее свободу перемещения рассматриваемого материального объекта, называется связью. Сила, с которой связь действует на тело (систему тел), называется силой реакции связи. Реакции связей заранее неизвестны, они зависят от приложенных к телу активных сил, т.е. носят пассивный характер. Если на тело связи не наложены, тело называется свободным.
При изучении покоя или движения несвободного тела это тело мысленно выделяют из системы окружающих тел. При этом механическое действие связей учитывают, вводя реакции связей. Такой приём обычно формулируют как принцип освобождаемости от связей:
Несвободное тело можно рассматривать как свободное, если отбросить
Связи, заменив их механическое действие на тело силами реакций связей.
Как уже говорилось, начнём с рассмотрения вопросов равновесия материальных тел, под которым (не вдаваясь пока в подробности) будем понимать состояние покоя тела по отношению к какому либо другому телу, например, по отношению к Земле.
1.1. Основные определения и аксиомы статики
В статике изучаются условия равновесия и методы преобразования одних силовых систем в другие, эквивалентные данным.
Определение 1.
Множество приложенных к телу сил называется системой сил.
Определение 2.
Две системы сил называются эквивалентными, если приложение каждой из них к одному и тому же покоящемуся свободному твёрдому телу приводит к одному и тому же движению:
Определение 3.
Система сил, под действием которой свободное твёрдое тело может оставаться в покое, называется уравновешенной или эквивалентной нулю:
Определение 4.
Если система сил эквивалентна одной силе, то эта сила называется равнодействующей системы сил:
Аксиомы устанавливают простейшие правила действия над силами и системами сил.
Аксиома 1.
Аксиома 2.
Аксиома 3.
Система двух сил, приложенных к абсолютно твёрдому телу, эквивалентна нулю тогда и только тогда, когда эти силы равны по модулю и действуют по одной прямой в противоположные стороны (Рис. 1.4).
Сформулированные аксиомы позволяют рассматривать систему сил, приложенную к абсолютно твёрдому телу, как систему скользящих векторов. В самом деле, аксиома 1 позволяет рассматривать силу как вектор. Покажем, что это вектор скользящий.
|
|
|
| Рис.1.5
|
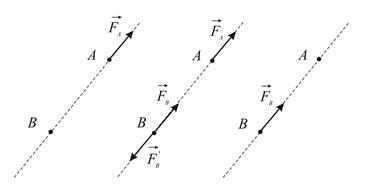
Пусть в точке A абсолютно твёрдого тела приложена сила 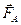 . Выберем на линии действия силы любую точку B, в которой приложим силы
. Выберем на линии действия силы любую точку B, в которой приложим силы  и
и 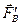 (Рис.1.5), причём
(Рис.1.5), причём  . На основании аксиом 1 и 2 получаем:
. На основании аксиом 1 и 2 получаем:  так как
так как  Но силы
Но силы 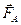 и
и 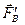 также образуют уравновешенную систему сил и, следовательно, могут быть отброшены.
также образуют уравновешенную систему сил и, следовательно, могут быть отброшены.
Таким образом,
ЛЕКЦИЯ 2
Пара сил
Существенную роль в изучении механического взаимодействия материальных тел играет простейшая силовая система, называемая парой сил.
Теорема
ОСНОВНЫЕ ТЕОРЕМЫ СТАТИКИ
Теорема.
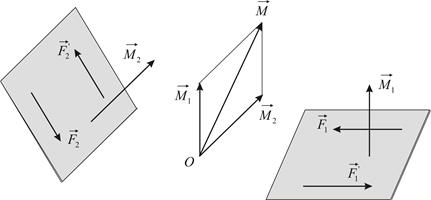
Произвольная система сил эквивалентна системе, состоящей из одной силы, равной геометрической сумме всех сил системы, приложенной в произвольно выбранной точке (центре приведения), и одной пары сил, момент которой равен сумме моментов всех сил системы относительно этой точки.

|
| Рис. 2.1
|
Доказательство. Пусть задана система сил  , произвольным образом расположенных в пространстве (Рис. 2.1). Выберем любую точку
, произвольным образом расположенных в пространстве (Рис. 2.1). Выберем любую точку 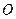 в качестве центра приведения. Рассмотрим любую силу системы
в качестве центра приведения. Рассмотрим любую силу системы  . На основании аксиомы 2 приложим к точке
. На основании аксиомы 2 приложим к точке 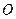 уравновешенную систему сил
уравновешенную систему сил  , причём,
, причём,  . Таким образом, сила
. Таким образом, сила  оказывается эквивалентной системе трёх сил, состоящей из такой же по модулю и направлению силы
оказывается эквивалентной системе трёх сил, состоящей из такой же по модулю и направлению силы  , приложенной в точке
, приложенной в точке 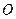 , и пары сил
, и пары сил  , момент которой равен моменту силы
, момент которой равен моменту силы  относительно точки
относительно точки 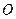 .
.
Проделывая такую операцию с каждой силой системы, заменяем заданную систему сил эквивалентной, которая состоит из приложенных в точке 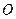 сил
сил  и пар сил
и пар сил  , плоскости действия которых имеют общую точку
, плоскости действия которых имеют общую точку 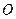 .
.
В соответствии с аксиомой 1 система сил  эквивалентна одной силе
эквивалентна одной силе  , приложенной в точке
, приложенной в точке 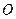 и равной геометрической сумме всех заданных сил:
и равной геометрической сумме всех заданных сил:
 .
.
В соответствии с теоремой о сложении пар система пар сил  эквивалентна одной паре, момент которой равен сумме моментов слагаемых пар, т.е. сумме моментов всех сил исходной системы относительно точки
эквивалентна одной паре, момент которой равен сумме моментов слагаемых пар, т.е. сумме моментов всех сил исходной системы относительно точки 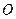 :
:
 .
.
Таким образом, установлены две важнейшие характеристики системы сил:
главным вектором системы сил называется геометрическая сумма всех сил системы:

главным моментом системы сил относительно некоторого центра O называется геометрическая сумма моментов всех сил системы относительно точки O:

Вектор главного момента изображают приложенным в той точке 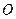 , относительно которой он вычисляется.
, относительно которой он вычисляется.
Заметим, что главный вектор и главный момент системы сил представляют собой чисто геометрические величины и не могут рассматриваться как некоторая сила или момент некоторой силы.
Доказанную выше теорему о приведении системы сил к одному центру теперь можно сформулировать в виде:
Произвольная система сил эквивалентна системе, состоящей из одной силы, равной главному вектору системы сил, приложенной в произвольно выбранной точке (центре приведения), и одной пары сил, момент которой равен главному моменту системы сил относительно этой точки.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
- Что называется парой сил?
- Что называется моментом пары сил?
- Как располагается вектор момента пары сил по отношению к паре сил?
- Чем можно заменить систему пар, плоскости действия которых пересекаются в одной точке?
- Чем заменяется любая система сил после её приведения к одному центру?
- Что называется главным вектором системы сил?
- Что общего и в чём различие между главным вектором и равнодействующей системы сил?
- Что называется главным моментом системы сил относительно центра?
ЛЕКЦИЯ 3
Теорема.
Система сил эквивалентна нулю (уравновешена) тогда и только тогда, когда её главный вектор и главный момент относительно произвольной точки равны нулю.
Доказательство. Приведём заданную систему сил к произвольно выбранному центру 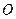 . В соответствии с теоремой о приведении системы сил к одному центру, исходная система сил эквивалентна одной силе
. В соответствии с теоремой о приведении системы сил к одному центру, исходная система сил эквивалентна одной силе 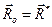 , приложенной в выбранном центре
, приложенной в выбранном центре 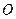 , и одной паре сил
, и одной паре сил  , момент которой
, момент которой  , т.е.
, т.е.
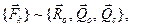 причём
причём 
Силы  и
и  заменим равнодействующей
заменим равнодействующей  (Рис. 2.2). Таким образом, любую систему сил можно заменить эквивалентной системой двух сил. При этом
(Рис. 2.2). Таким образом, любую систему сил можно заменить эквивалентной системой двух сил. При этом
 (a)
(a)
 (b)
(b)
Аксиома 2 устанавливает необходимые и достаточные условия равновесия системы двух сил, приложенных к абсолютно твёрдому телу – силы должны быть равными по модулю, противоположными по направлению  и, кроме того, должны иметь общую линию действия (Рис. 2.3), т.е.
и, кроме того, должны иметь общую линию действия (Рис. 2.3), т.е. 

|
| 
|
| Рис. 2.2
|
| Рис. 2.3
|
|
|
|
|
Сравнивая последние равенства с равенствами (a) и (b), находим, что для равновесия произвольной системы сил необходимо и достаточно, чтобы геометрическая сумма всех сил системы (главный вектор) равнялась нулю и сумма моментов всех сил системы относительно произвольно выбранной точки (главный момент) равнялась нулю:

Принимая центр приведения за начало декартовой системы координат, получаем в проекциях на координатные оси:


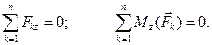
Таким образом,
Для равновесия произвольной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из трёх взаимно перпендикулярных осей координат равнялась нулю и сумма моментов всех сил системы относительно каждой из этих осей равнялась нулю.
Эквивалентность систем сил
Теорема.
Две системы сил, приложенные к свободному твёрдому телу, эквивалентны тогда и только тогда, когда их главные векторы и главные моменты относительно одного и того же произвольно выбранного центра равны между собой.
Доказательство. Пусть две системы сил эквивалентны:  Покажем, что главные векторы и главные моменты этих систем сил равны между собой. Используя принцип независимости действия сил, выберем вспомогательную систему сил
Покажем, что главные векторы и главные моменты этих систем сил равны между собой. Используя принцип независимости действия сил, выберем вспомогательную систему сил  такую, что
такую, что  и, следовательно,
и, следовательно,  . При этом действие заданных систем сил на тело (в составе новых систем сил) не изменяется. Условия равновесия для расширенных систем сил имеют вид:
. При этом действие заданных систем сил на тело (в составе новых систем сил) не изменяется. Условия равновесия для расширенных систем сил имеют вид:



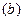
Сравнивая равенства  и
и 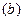 , получаем:
, получаем:
 или
или 

Таким образом, доказана необходимость условий  для эквивалентности систем сил.
для эквивалентности систем сил.
Докажем достаточность. Пусть условия  выполнены. Покажем, что системы сил при этом эквивалентны. Рассмотрим вспомогательную систему сил
выполнены. Покажем, что системы сил при этом эквивалентны. Рассмотрим вспомогательную систему сил  , для которой справедливы равенства
, для которой справедливы равенства  , и, следовательно, справедливы равенства
, и, следовательно, справедливы равенства 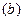 . На основании теоремы об условиях равновесия системы сил отсюда получаем
. На основании теоремы об условиях равновесия системы сил отсюда получаем
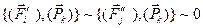 .
.
На основании аксиомы 2 к любой системе сил можно добавить или от неё отнять уравновешенную систему сил. Отсюда:

Теорема Вариньона
Из теоремы об эквивалентности вытекает очень важное следствие, которое в литературе обычно формулируют как теорему Вариньона:
Основные свойства пары сил
В соответствии с теоремой об эквивалентности систем сил, две пары сил эквивалентны тогда и только тогда, когда равны их моменты. Отсюда следует, что, не изменяя действия пары сил на абсолютно твёрдое тело, можно производить следующие преобразования пар сил (Рис. 2.4 – 2.6):
1. переносить и поворачивать пару сил в плоскости её действия;
2. переносить пару сил в любую плоскость, параллельную плоскости
действия пары сил;
3. изменять плечо и модули сил, образующих пару, так чтобы модуль
момента пары оставался неизменным.

|
| 
|
| 
|
| Рис. 2.4
|
| Рис. 2.5
|
| Рис. 2.6
|
|
|
|
|
|
|
Доказанная ранее теорема о сложении пар оказывается справедливой при произвольном расположении пар сил в пространстве, поскольку в случае параллельности плоскостей действия, пары сил можно перенести в одну плоскость.
|
|
|
| Рис. 2.7
|
Таким образом,
ЛЕКЦИЯ 4
Центр параллельных сил
При изучении объёмных и поверхностных сил широко используется центр параллельных сил. Это понятие вводится для системы параллельных сил, имеющих равнодействующую, причём точки приложения сил системы  считаются фиксированными.
считаются фиксированными.
Центром параллельных сил называется точка, вокруг которой поворачивается равнодействующая системы параллельных сил при повороте всех сил системы вокруг своих точек приложения в одну и ту же сторону на один и тот же угол.
|
|
|
| Рис.3.1
|
Найдём положение центра параллельных сил 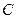 для системы
для системы  , имеющей равнодействующую
, имеющей равнодействующую 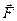 . Пусть
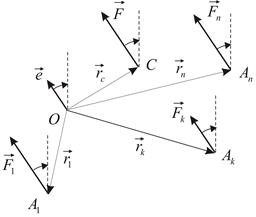
. Пусть 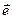 – единичный вектор, параллельный линиям действия сил системы (Рис. 3.1). Тогда
– единичный вектор, параллельный линиям действия сил системы (Рис. 3.1). Тогда 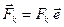 , где
, где  – проекция силы на направление единичного вектора
– проекция силы на направление единичного вектора  . Для равнодействующей получаем:
. Для равнодействующей получаем:

Для любого центра 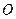 , используя теорему Вариньона, получаем:
, используя теорему Вариньона, получаем:

или 
Вынося за скобку общий множитель 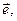 получаем:
получаем:
 или
или  где
где 
Векторное произведение равно нулю, если один из сомножителей равен нулю или если сомножители коллинеарны. Но 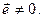 Повернём все силы системы вокруг своих точек приложения в одну и ту же сторону на один и тот же угол (Рис. 3.1). Равнодействующая системы сил повернётся вокруг точки C в ту же сторону на тот же угол. Вместе с силами поворачивается вокруг точки O и вектор
Повернём все силы системы вокруг своих точек приложения в одну и ту же сторону на один и тот же угол (Рис. 3.1). Равнодействующая системы сил повернётся вокруг точки C в ту же сторону на тот же угол. Вместе с силами поворачивается вокруг точки O и вектор 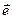 . В результате этой операции вектор
. В результате этой операции вектор 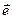 изменил направление; вектор
изменил направление; вектор 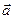 остался неизменным, но по-прежнему
остался неизменным, но по-прежнему 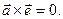 Следовательно,
Следовательно,  т.е.
т.е.
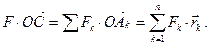
Отсюда
 (1)
(1)
Примем точку O за начало декартовой системы координат. Записывая формулу (1) в проекциях на координатные оси, получаем координаты центра параллельных сил:

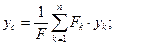
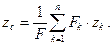
Центр тяжести
Пример 3.1.
Определить положение центра тяжести однородной пластины,
изображённой на Рис. 3.3.

|
| Рис. 3.3
|
|
|
Разобьём пластину на два прямоугольника с площадями 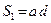 и
и  Прямоугольники обладают осевой симметрией и их центры тяжести находятся в точке пересечения диагоналей
Прямоугольники обладают осевой симметрией и их центры тяжести находятся в точке пересечения диагоналей
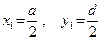 и
и 
Для однородной пластины постоянной толщины вес пропорционален площади поверхности. В проекциях на координатные оси из формулы (2) получаем:
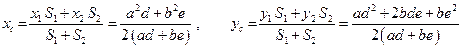 .
.
Метод дополнений или метод отрицательных масс представляет собой частный случай метода разбиений, применяется для тел имеющих вырезы (полости), вес которых (для однородных тел – объём или площадь) считается отрицательным.
Пример 3.2.
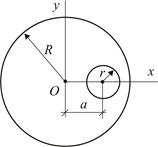
Определить положение центра тяжести однородной пластины, изображённой на Рис. 3.4.
Прежде всего заметим, что пластина имеет ось симметрии, проходящую через центр пластины и центр выреза. Примем эту ось за координатную ось 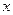 . Тогда
. Тогда 
Разобьём пластину на две части: круг без выреза радиуса  и вырез радиуса
и вырез радиуса  с центром
с центром 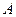 . При этом
. При этом 
Используя формулу (2), получаем:

|
|

|
|
|
|
|
| Рис. 3.4
|
| Рис. 3/5
|
Пример 3.3.
Определить положение центра тяжести однородной треугольной пластины, изображённой на Рис. 3.5.
Разобьём треугольник на элементарные полоски, параллельные одной из сторон, например, стороне 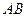 . Центр тяжести каждой полоски в силу симметрии лежит на её середине, а центр тяжести треугольники расположен, следовательно, на медиане
. Центр тяжести каждой полоски в силу симметрии лежит на её середине, а центр тяжести треугольники расположен, следовательно, на медиане  . Проводя аналогичное разбиение параллельно другой стороне, например
. Проводя аналогичное разбиение параллельно другой стороне, например  , получаем, что центр тяжести лежит на медиане
, получаем, что центр тяжести лежит на медиане  . Таким образом, центр тяжести однородного треугольника расположен в точке пересечения его медиан.
. Таким образом, центр тяжести однородного треугольника расположен в точке пересечения его медиан.
Пример 3.4.
Определить положение центра тяжести однородной дуги
окружности радиуса  с центральным углом
с центральным углом 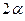 (Рис. 3.6).
(Рис. 3.6).
Начало координат совместим с центром окружности, ось 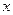 направим перпендикулярно хорде
направим перпендикулярно хорде 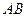 , стягивающей дугу. В этом случае ось
, стягивающей дугу. В этом случае ось 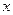 будет осью симметрии тела и, следовательно,
будет осью симметрии тела и, следовательно,  . Для вычисления
. Для вычисления  используем формулу (6):
используем формулу (6):
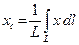 причём,
причём, 
Тогда


|
| 
|
|
|
|
|
| Рис. 3.6
|
| Рис. 3.7
|
Пример 3.5.
Определить положение центра тяжести однородного кругового сектора радиуса  с центральным углом
с центральным углом  (Рис. 3.7).
(Рис. 3.7).
Разобьём пластину на элементарные круговые секторы. Каждый элементарный сектор можно рассматривать как равнобедренный треугольник, центр тяжести которого расположен в точке пересечения медиан, которые, как известно, делятся точкой пересечения в отношении 2:1. Таким образом, центр тяжести рассматриваемого кругового сектора совпадает с центром тяжести однородной дуги окружности радиуса  и таким же центральным углом. Используя результат, полученный в предыдущем примере, находим:
и таким же центральным углом. Используя результат, полученный в предыдущем примере, находим:
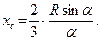
Положение центра тяжести играет важную роль в вопросах устойчивости и предотвращения опрокидывания сооружений.
В заключение заметим, что при определении положения центра тяжести как вид результата, так и трудоёмкость его получения существенно зависят от выбора системы координат.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
- Что называется центром параллельных сил?
- По каким формулам определяются координаты центра параллельных сил?
- Что называется центром тяжести тела?
- В чём состоит метод разбиений для вычисления координат центра тяжести тела?
- В чём состоит метод отрицательных масс для вычисления координат центра тяжести тела?
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплект СР-14.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1
Плоскости
В дальнейшем на лекциях будет показано, что
Для равновесия системы сил, линии действия которых расположены в одной плоскости, необходимо и достаточно, чтобы сумма проекций всех сил на каждую из двух взаимно перпендикулярных осей, лежащих в плоскости действия сил, равнялась нулю и сумма моментов всех сил относительно оси, перпендикулярной плоскости действия сил, равнялась нулю
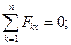
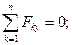
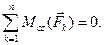 (1.1)
(1.1)
где 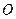 – произвольно выбранная точка плоскости
– произвольно выбранная точка плоскости 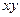 .
.
В курсе статики используется, в основном, декартова система координат, три взаимно перпендикулярных оси которой – 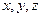 , имеют орты
, имеют орты  .
.
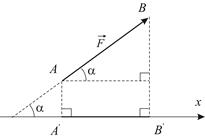
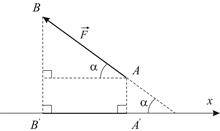
Первые два уравнения равновесия (1.1) связывают проекции векторов сил на выбранные координатные оси. Чтобы построить такую проекцию, нужно перенести ось параллельно самой себе так, чтобы она проходила через точку приложения силы и опустить перпендикуляры на ось из начала и конца вектора (Рис. 1.1-1.2):
проекцией вектора 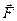 на координатную ось
на координатную ось 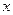 называется взятая с соответствующим знаком длина отрезка оси, заключённого между проекциями начала и конца вектора
называется взятая с соответствующим знаком длина отрезка оси, заключённого между проекциями начала и конца вектора
|
| 
|
|
|
|
|
| Рис. 1.1
|
| Рис. 1.2
|
Таким образом, ортогональная проекция вектора силы 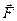 на ось
на ось 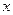 определяется по формуле
определяется по формуле
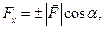
где  – модуль силы;
– модуль силы; 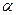 – острый угол между двумя прямыми: линией действия вектора
– острый угол между двумя прямыми: линией действия вектора 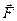 и осью
и осью 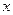 .
.
При этом проекция положительна, если условное перемещение от проекции начала вектора 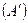 к проекции его конца
к проекции его конца 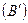 совпадает с положительным направлением оси
совпадает с положительным направлением оси 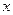 и отрицательна в противоположном случае.
и отрицательна в противоположном случае.
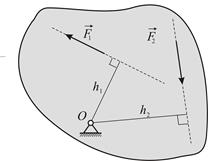
Третье уравнение (1.1) связывает так называемые моменты сил. Рассмотрим некоторую пластину, которая может вращаться вокруг оси  , проходящей через закреплённую точку
, проходящей через закреплённую точку 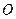 перпендикулярно плоскости пластины (Рис. 1.3). К пластине приложены две силы,
перпендикулярно плоскости пластины (Рис. 1.3). К пластине приложены две силы,
|
|
|
| Рис. 1.3
|
которые стремятся вращать пластину в противоположные стороны. Куда будет вращаться пластина? Опыт показывает, что вращательный эффект силы зависит не только от её величины, но и от её расположения по отношению к оси. Вращательный эффект силы характеризует её момент относительно оси  :
:
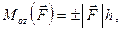
где 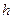 – плечо силы, равное кратчайшему расстоянию от точки
– плечо силы, равное кратчайшему расстоянию от точки 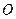 до линии действия силы; знак «+» соответствует повороту вокруг точки
до линии действия силы; знак «+» соответствует повороту вокруг точки 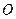 против хода часовой стрелки.
против хода часовой стрелки.
Напомним, что мы говорим о силах, линии действия которых расположены в плоскости, перпендикулярной оси  . В дальнейшем будут введены общие понятия момента силы относительно точки и оси.
. В дальнейшем будут введены общие понятия момента силы относительно точки и оси.
Основные виды связей
Помимо заданных – активных сил – на тело, равновесие которого рассматривается, действуют силы, приложенные со стороны опор – связей. Реакция связи потому так и называется потому, что возникает в ответ – реагирует на действие сил, приложенных к телу. В зависимости от устройства связи обладают различными возможностями по ограничению перемещения точки закрепления.
Рассмотрим некоторые из так называемых идеальных связей. Понятие идеальных связей – важнейшее понятие механики будет подробно рассмотрено в дальнейшем при изучении аналитической механики. Пока будем считать связь идеальной, если возможно не учитывать явление трения.
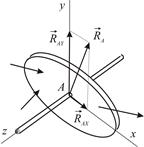
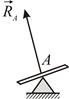
Одна из самых распространённых опор – н еподвижный цилиндрический шарнир (подшипник). Простейшую схему такой опоры можно представить следующим образом: имеется закреплённый стержень, на который надета пластина (Рис. 1.4). Такая опора позволяет пластине скользить вдоль стержня и вращаться вокруг него. Под действием активной нагрузки возникает точечный контакт между стержнем и пластиной. Реакция направлена по нормали к стержню (оси шарнира), но заранее неизвестно в какой точке осуществляется контакт и, следовательно, по какой из нормалей к оси шарнира будет направлена реакция.
|
| 
|
|
|
|
|
| Рис. 1.4
|
| Рис.1.5
|
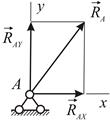
Таким образом, в общем случае реакция неподвижного шарнира расположена в плоскости, перпендикулярной оси шарнира, но в этой плоскости она заранее неизвестна ни по модулю, ни по направлению. Для её определения удобно ввести две неизвестные по модулю составляющие, направленные параллельно координатным осям в положительном направлении этих осей 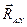 и
и  . Неизвестными величинами в таком случае будут проекции силы реакции шарнира на координатные оси
. Неизвестными величинами в таком случае будут проекции силы реакции шарнира на координатные оси 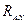 и
и 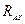 .
.
Размерами шарнира при расчётах пренебрегают. Схематическое изображение неподвижного шарнира представлено на Рис. 1.5. Конструктивно неподвижный цилиндрический шарнир, как правило, представляет собой шарикоподшипник.
Для некоторых видов опор перемещения точки закрепления ограничиваются только в определённом направлении. По этому направлению и действует сила реакции связей. В качестве неизвестной величины для опор такого типа имеет смысл рассматривать модуль реакции опоры.
Рассмотрим опоры, относящиеся к такому типу.
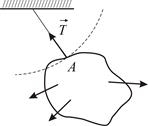
Гибкая невесомая нерастяжимая нить. Нить не даёт телу перемещаться в единственном направлении – вдоль нити от точки закрепления (на растяжение нити). Реакция такой нити 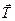 всегда направлена вдоль нити к точке подвеса (Рис.1.6).
всегда направлена вдоль нити к точке подвеса (Рис.1.6).
|
| 
|
|
|
|
|
| Рис. 1.6
|
| Рис. 1.7
|
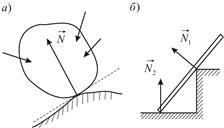
Гладкая (без трения) поверхность. Реакция такой поверхности направлена по общей нормали к поверхностям тел, проведённой в точке контакта, причём наружу от опорной поверхности (Рис.1.7а). Если в точке контакта у одной из поверхностей нормаль не определена (Рис.1.7б), то реакция направлена по нормали к другой поверхности.
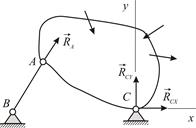
Невесомый ненагруженный стержень с шарнирно закреплёнными концами. Пусть тело закреплено при помощи неподвижного шарнира 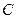 и невесомого стержня
и невесомого стержня 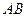 , шарнирно закреплённого на концах (Рис. 1.8).
, шарнирно закреплённого на концах (Рис. 1.8).
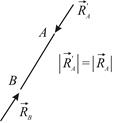
Рассмотрим стержень 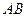 (Рис.1.9). Он находится в равновесии под действием двух сил, приложенных в точках
(Рис.1.9). Он находится в равновесии под действием двух сил, приложенных в точках 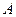 и
и 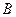 . Две силы могут уравновесить друг друга только в том случае, когда они действуют по одной прямой. Таким образом, сила давления тела на стержень
. Две силы могут уравновесить друг друга только в том случае, когда они действуют по одной прямой. Таким образом, сила давления тела на стержень 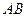 направлена вдоль стержня. Учитывая третий закон Ньютона, приходим к выводу, что реакция ненагруженного стержня направлена вдоль прямой, соединяющей шарнирно закреплённые концы стержня.
направлена вдоль стержня. Учитывая третий закон Ньютона, приходим к выводу, что реакция ненагруженного стержня направлена вдоль прямой, соединяющей шарнирно закреплённые концы стержня.
|
| 
|
|
|
|
|
| Рис. 1.8
|
| Рис. 1.9.
|
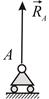
Схематическое изображение такой опоры и её реакция представлены на Рис.1.10.
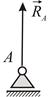
Подвижный цилиндрический шарнир представляет собой цилиндрический шарнир, поставленный на катки, на которых он может без сопротивления перемещаться по опорной поверхности. Реакция направлена по нормали к опорной поверхности (Рис.1.11).

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Рис.1.10
|
| Рис.1.11
|
| Рис.1.12
|
| Рис.1.13
|
| Рис.1.14
|
Аналогичные реакции возникают в шарнирно-скользящей опоре (Рис.1.12) и игольчатой опоре (Рис.1.13).
Заметим, что шарнирно-неподвижную опору (Рис.1.5) можно представить как систему двух шарнирно закреплённых на концах стержней (Рис.1.14).
Пример 1.1
Балка 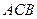 имеет шарнирно неподвижную опору в точке
имеет шарнирно неподвижную опору в точке 
|
|
|






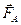 . Выберем на линии действия силы любую точку B, в которой приложим силы
. Выберем на линии действия силы любую точку B, в которой приложим силы  и
и 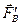 (Рис.1.5), причём
(Рис.1.5), причём  . На основании аксиом 1 и 2 получаем:
. На основании аксиом 1 и 2 получаем:  так как
так как  Но силы
Но силы 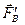 также образуют уравновешенную систему сил и, следовательно, могут быть отброшены.
также образуют уравновешенную систему сил и, следовательно, могут быть отброшены.
 , произвольным образом расположенных в пространстве (Рис. 2.1). Выберем любую точку
, произвольным образом расположенных в пространстве (Рис. 2.1). Выберем любую точку 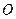 в качестве центра приведения. Рассмотрим любую силу системы
в качестве центра приведения. Рассмотрим любую силу системы  . На основании аксиомы 2 приложим к точке
. На основании аксиомы 2 приложим к точке  , причём,
, причём,  . Таким образом, сила
. Таким образом, сила  , приложенной в точке
, приложенной в точке  , момент которой равен моменту силы
, момент которой равен моменту силы  и пар сил
и пар сил  , плоскости действия которых имеют общую точку
, плоскости действия которых имеют общую точку  , приложенной в точке
, приложенной в точке  .
. .
.


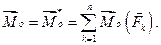
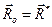 , приложенной в выбранном центре
, приложенной в выбранном центре  , момент которой
, момент которой  , т.е.
, т.е.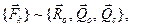 причём
причём 
 заменим равнодействующей
заменим равнодействующей  (Рис. 2.2). Таким образом, любую систему сил можно заменить эквивалентной системой двух сил. При этом
(Рис. 2.2). Таким образом, любую систему сил можно заменить эквивалентной системой двух сил. При этом (a)
(a) (b)
(b) и, кроме того, должны иметь общую линию действия (Рис. 2.3), т.е.
и, кроме того, должны иметь общую линию действия (Рис. 2.3), т.е. 





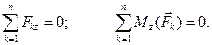
 Покажем, что главные векторы и главные моменты этих систем сил равны между собой. Используя принцип независимости действия сил, выберем вспомогательную систему сил
Покажем, что главные векторы и главные моменты этих систем сил равны между собой. Используя принцип независимости действия сил, выберем вспомогательную систему сил  такую, что
такую, что  и, следовательно,
и, следовательно,  . При этом действие заданных систем сил на тело (в составе новых систем сил) не изменяется. Условия равновесия для расширенных систем сил имеют вид:
. При этом действие заданных систем сил на тело (в составе новых систем сил) не изменяется. Условия равновесия для расширенных систем сил имеют вид:


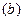
 или
или 

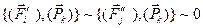 .
.




 считаются фиксированными.
считаются фиксированными.
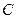 для системы
для системы  , имеющей равнодействующую
, имеющей равнодействующую 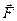 . Пусть
. Пусть 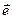 – единичный вектор, параллельный линиям действия сил системы (Рис. 3.1). Тогда
– единичный вектор, параллельный линиям действия сил системы (Рис. 3.1). Тогда 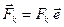 , где
, где  – проекция силы на направление единичного вектора
– проекция силы на направление единичного вектора  . Для равнодействующей получаем:
. Для равнодействующей получаем:


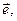 получаем:
получаем: или
или  где
где 
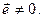 Повернём все силы системы вокруг своих точек приложения в одну и ту же сторону на один и тот же угол (Рис. 3.1). Равнодействующая системы сил повернётся вокруг точки C в ту же сторону на тот же угол. Вместе с силами поворачивается вокруг точки O и вектор
Повернём все силы системы вокруг своих точек приложения в одну и ту же сторону на один и тот же угол (Рис. 3.1). Равнодействующая системы сил повернётся вокруг точки C в ту же сторону на тот же угол. Вместе с силами поворачивается вокруг точки O и вектор 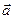 остался неизменным, но по-прежнему
остался неизменным, но по-прежнему 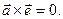 Следовательно,
Следовательно,  т.е.
т.е.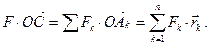
 (1)
(1)
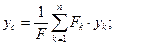
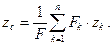

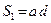 и
и  Прямоугольники обладают осевой симметрией и их центры тяжести находятся в точке пересечения диагоналей
Прямоугольники обладают осевой симметрией и их центры тяжести находятся в точке пересечения диагоналей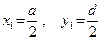 и
и 
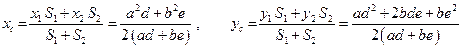 .
.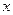 . Тогда
. Тогда 
 и вырез радиуса
и вырез радиуса  с центром
с центром 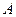 . При этом
. При этом 



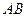 . Центр тяжести каждой полоски в силу симметрии лежит на её середине, а центр тяжести треугольники расположен, следовательно, на медиане
. Центр тяжести каждой полоски в силу симметрии лежит на её середине, а центр тяжести треугольники расположен, следовательно, на медиане  . Проводя аналогичное разбиение параллельно другой стороне, например
. Проводя аналогичное разбиение параллельно другой стороне, например  , получаем, что центр тяжести лежит на медиане
, получаем, что центр тяжести лежит на медиане  . Таким образом, центр тяжести однородного треугольника расположен в точке пересечения его медиан.
. Таким образом, центр тяжести однородного треугольника расположен в точке пересечения его медиан.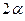 (Рис. 3.6).
(Рис. 3.6). . Для вычисления
. Для вычисления  используем формулу (6):
используем формулу (6):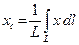 причём,
причём, 



 (Рис. 3.7).
(Рис. 3.7). и таким же центральным углом. Используя результат, полученный в предыдущем примере, находим:
и таким же центральным углом. Используя результат, полученный в предыдущем примере, находим: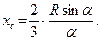
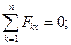
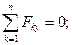
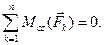 (1.1)
(1.1)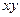 .
.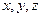 , имеют орты
, имеют орты  .
.

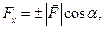
 – модуль силы;
– модуль силы; 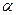 – острый угол между двумя прямыми: линией действия вектора
– острый угол между двумя прямыми: линией действия вектора 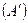 к проекции его конца
к проекции его конца 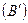 совпадает с положительным направлением оси
совпадает с положительным направлением оси  , проходящей через закреплённую точку
, проходящей через закреплённую точку 
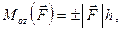
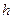 – плечо силы, равное кратчайшему расстоянию от точки
– плечо силы, равное кратчайшему расстоянию от точки 

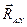 и
и  . Неизвестными величинами в таком случае будут проекции силы реакции шарнира на координатные оси
. Неизвестными величинами в таком случае будут проекции силы реакции шарнира на координатные оси 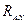 и
и 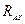 .
.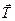 всегда направлена вдоль нити к точке подвеса (Рис.1.6).
всегда направлена вдоль нити к точке подвеса (Рис.1.6).

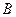 . Две силы могут уравновесить друг друга только в том случае, когда они действуют по одной прямой. Таким образом, сила давления тела на стержень
. Две силы могут уравновесить друг друга только в том случае, когда они действуют по одной прямой. Таким образом, сила давления тела на стержень 






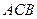 имеет шарнирно неподвижную опору в точке
имеет шарнирно неподвижную опору в точке 

