(несобственные интегралы первого рода)
Пусть функция f (x) определена на полуоси  и интегрируема по любому отрезку [ a, b ], принадлежащему этой полуоси. Предел интеграла
и интегрируема по любому отрезку [ a, b ], принадлежащему этой полуоси. Предел интеграла  при
при  называется несобственным интегралом функции f (x) от a до
называется несобственным интегралом функции f (x) от a до 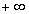 и обозначается
и обозначается  .
.
Итак, по определению,  . Если этот предел существует и конечен, интеграл
. Если этот предел существует и конечен, интеграл  называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.
называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.
Пример 1.
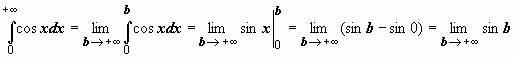 ;
;
этот предел не существует; следовательно, исследуемый интеграл расходится.
Пример 2. 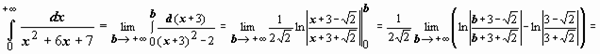
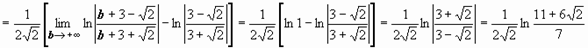 ; следовательно, интеграл сходится и равен
; следовательно, интеграл сходится и равен 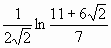 .
.
Аналогично интегралу с бесконечным верхним пределом интегрирования определяется интеграл в пределах от 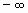 до b:
до b: 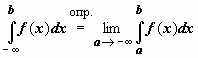 и в пределах от
и в пределах от 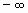 до
до 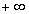 :
: 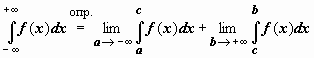 . В последнем случае f (x) определена на всей числовой оси, интегрируема по любому отрезку; c - произвольная (собственная) точка числовой оси; интеграл называется сходящимся, если существуют и конечны оба входящих в определение предела. Существование конечных пределов и их сумма не зависят от выбора точки c.
. В последнем случае f (x) определена на всей числовой оси, интегрируема по любому отрезку; c - произвольная (собственная) точка числовой оси; интеграл называется сходящимся, если существуют и конечны оба входящих в определение предела. Существование конечных пределов и их сумма не зависят от выбора точки c.
Пример 3.
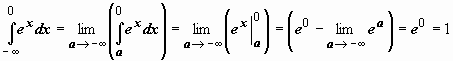 . Интеграл сходится.
. Интеграл сходится.
Пример 4. 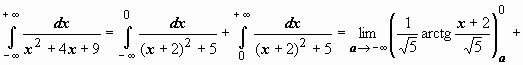
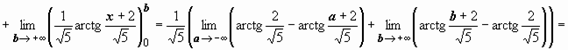
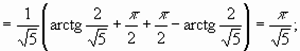 следовательно, интеграл сходится и равен
следовательно, интеграл сходится и равен 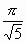 .
.
Формула Ньютона-Лейбница для несобственного интеграла.
Символом 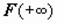 будем обозначать
будем обозначать 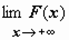 ; символом
; символом 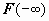 - соответственно,
- соответственно, 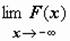 ; тогда можно записать
; тогда можно записать
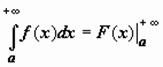 ,
, 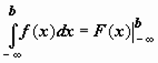 ,
, 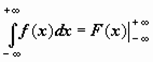 ,
,
подразумевая в каждом из этих случаев существование и конечность соответствующих пределов.
Теперь решения примеров выглядят более просто: 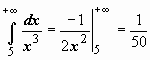 - интеграл сходится;
- интеграл сходится; 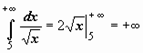 - интеграл расходится.
- интеграл расходится.
Для несобственных интегралов применимы формулы интегрирования по частям и замены переменной:
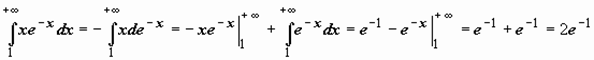
при замене переменной несобственный интеграл может преобразовываться в собственный.
Несобственные интегралы от неограниченных функций
(несобственные интегралы второго рода)
Пусть функция f (x) определена на полуинтервале (a, b ], интегрируема по любому отрезку  , и имеет бесконечный предел при
, и имеет бесконечный предел при  . Несобственным интегралом от f (x) по отрезку [ a, b ] называется предел
. Несобственным интегралом от f (x) по отрезку [ a, b ] называется предел  . Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится.
. Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится.
Пример 5.  - интеграл расходится;
- интеграл расходится;
Пример 6.
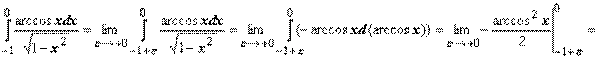
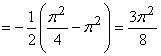 - интеграл сходится.
- интеграл сходится.
Применение формулы Ньютона-Лейбница.
Если для функции f (x) на полуинтервале (a, b ] существует первообразная F (x), то
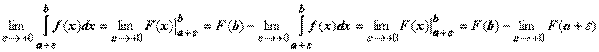 , и сходимость интеграла определяется наличием или отсутствием конечного предела
, и сходимость интеграла определяется наличием или отсутствием конечного предела 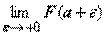 . Будем писать просто
. Будем писать просто 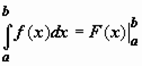 , имея в виду, что если соответствующий предел конечен, то интеграл сходится, в противном случае - расходится.
, имея в виду, что если соответствующий предел конечен, то интеграл сходится, в противном случае - расходится.
Пример 7. 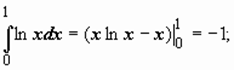 интеграл сходится.
интеграл сходится.
Пример 8. 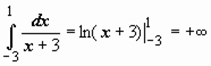 ; интеграл расходится.
; интеграл расходится.
Задание для самостоятельной работы
Вычислите несобственные интегралы:
1. 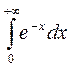 2.
2. 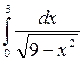 3.
3. 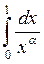 4.
4. 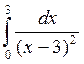 5.
5. 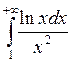
6. 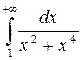 7.
7. 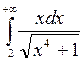 8.
8. 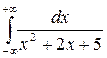
Рекомендуемая литература: 11.1 [с. 271-282], 1.2 [с. 205-212], 2.2 [с. 247-250].
Самостоятельная работа №8
Тема: Частные производные функций нескольких действительных переменных
Цель: закрепление и систематизация знаний по теме «Приложения частных производных».
Время выполнения: 6 часов
Теоретический материал
В природе иногда встречаются процессы, в которых исследуемая величина является функцией двух, трех и т. д. других величин. Так, в термодинамике температура идеального газа T зависит от давления p и объема V. Если каждому набору аргументов 
 …,
…,  ставится в соответствие число
ставится в соответствие число  то говорят, что задана функция n переменных
то говорят, что задана функция n переменных
Число A называется пределом функции f (x 1, x 2, …, xn) по подмножеству M области определения функции при (x 1; x 2; …; xn) → (a 1; a 2; …; an), если для любого ε > 0 существует такое δ > 0, что на пересечении δ-окрестности точки A (кроме, быть может, самой точки A) с подмножеством M для всех x = (x 1; x 2; …; xn) выполняется неравенство
В этом случае пишут 
Пусть функция двух переменных f (x, y) определена в некоторой окрестности точки (x 0; y 0). Пределом функции f (x, y) в точке (x 0; y 0) по направлению l = (cos α, sin α) называется число
где L – луч, выходящий из точки (x 0; y 0) в направлении l.
Пусть функция f (x 1, x 2, …, xn) определена в окрестности точки a = (a 1; a 2; …; an). Рассмотрим функцию одной переменной f (x 1, a 2, …, an). Она может иметь производную по своей переменной x 1. Такая производная по определению называется частной производной  в точке
в точке 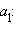
Аналогично определяются частные производные функции f по другим переменным. Поскольку при вычислении частных производных все переменные, кроме одной, фиксируются, правила вычисления частной производной точно такие же, как и обычной производной.
Задание для самостоятельной работы
Подготовить сообщение на тему «Приложения частных производных».
Рекомендуемая литература: 1.2 [с. 438-439], 2.2 [с. 151-166].
Самостоятельная работа №9
Тема: Вычисление двойных интегралов
Цель: формирование умений изменять порядок интегрирования, вычислять двойные интегралы в декартовых координатах.
Время выполнения: 7 часов (для 09.02.03, 09.02.04), 8 часов для (09.02.01)
Теоретический материал

Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е - результат первого интегрирования интегрируем по х в пределах от а до b.

Здесь, при вычислении внутреннего интеграла, считаем у постоянным.
Пример 1. Поменять порядок интегрирования:

Решение:
Изобразим область интегрирования.
Итак, х изменяется от 0 до 1, т.е. от прямой х=0 до прямой х=1, а у изменяется от 0 до х, т.е. от прямой у=0 до прямой у=х. Получим:

Рис.8. Область интегрирования  .
.
Интеграл
 взят в направлении вдоль оси Оу, изменив направление вдоль оси Ох мы получим:
взят в направлении вдоль оси Оу, изменив направление вдоль оси Ох мы получим:

Объем тела

где  - уравнение поверхности, ограничивающей тело сверху.
- уравнение поверхности, ограничивающей тело сверху.
Площадь плоской фигуры

Масса плоской фигуры
Масса плоской фигуры D с переменной плотностью  находится по формуле
находится по формуле




 и интегрируема по любому отрезку [ a, b ], принадлежащему этой полуоси. Предел интеграла
и интегрируема по любому отрезку [ a, b ], принадлежащему этой полуоси. Предел интеграла  при
при  называется несобственным интегралом функции f (x) от a до
называется несобственным интегралом функции f (x) от a до 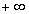 и обозначается
и обозначается  .
. . Если этот предел существует и конечен, интеграл
. Если этот предел существует и конечен, интеграл  называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.
называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.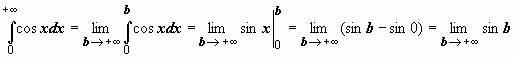 ;
;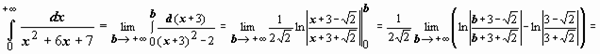
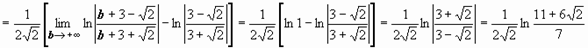 ; следовательно, интеграл сходится и равен
; следовательно, интеграл сходится и равен 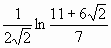 .
.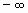 до b:
до b: 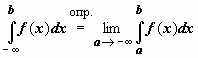 и в пределах от
и в пределах от 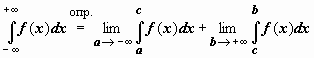 . В последнем случае f (x) определена на всей числовой оси, интегрируема по любому отрезку; c - произвольная (собственная) точка числовой оси; интеграл называется сходящимся, если существуют и конечны оба входящих в определение предела. Существование конечных пределов и их сумма не зависят от выбора точки c.
. В последнем случае f (x) определена на всей числовой оси, интегрируема по любому отрезку; c - произвольная (собственная) точка числовой оси; интеграл называется сходящимся, если существуют и конечны оба входящих в определение предела. Существование конечных пределов и их сумма не зависят от выбора точки c.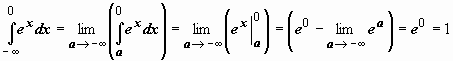 . Интеграл сходится.
. Интеграл сходится.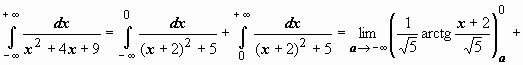
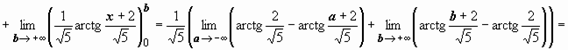
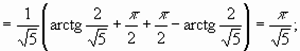 следовательно, интеграл сходится и равен
следовательно, интеграл сходится и равен 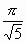 .
.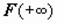 будем обозначать
будем обозначать 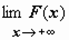 ; символом
; символом 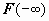 - соответственно,
- соответственно, 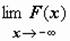 ; тогда можно записать
; тогда можно записать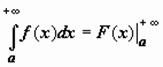 ,
, 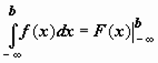 ,
, 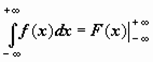 ,
,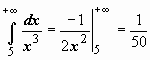 - интеграл сходится;
- интеграл сходится; 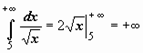 - интеграл расходится.
- интеграл расходится.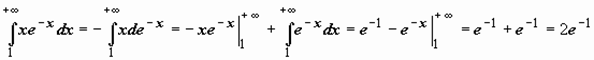
 , и имеет бесконечный предел при
, и имеет бесконечный предел при  . Несобственным интегралом от f (x) по отрезку [ a, b ] называется предел
. Несобственным интегралом от f (x) по отрезку [ a, b ] называется предел  . Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится.
. Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится. - интеграл расходится;
- интеграл расходится;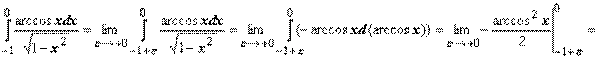
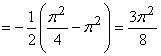 - интеграл сходится.
- интеграл сходится.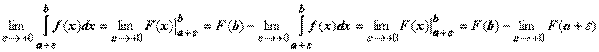 , и сходимость интеграла определяется наличием или отсутствием конечного предела
, и сходимость интеграла определяется наличием или отсутствием конечного предела 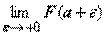 . Будем писать просто
. Будем писать просто 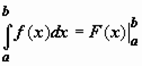 , имея в виду, что если соответствующий предел конечен, то интеграл сходится, в противном случае - расходится.
, имея в виду, что если соответствующий предел конечен, то интеграл сходится, в противном случае - расходится.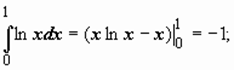 интеграл сходится.
интеграл сходится.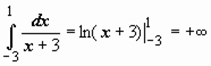 ; интеграл расходится.
; интеграл расходится.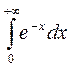 2.
2. 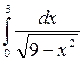 3.
3. 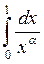 4.
4. 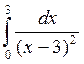 5.
5. 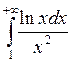
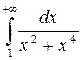 7.
7. 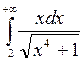 8.
8. 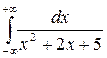

 …,
…,  ставится в соответствие число
ставится в соответствие число  то говорят, что задана функция n переменных
то говорят, что задана функция n переменных

 в точке
в точке 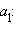





 взят в направлении вдоль оси Оу, изменив направление вдоль оси Ох мы получим:
взят в направлении вдоль оси Оу, изменив направление вдоль оси Ох мы получим:

 - уравнение поверхности, ограничивающей тело сверху.
- уравнение поверхности, ограничивающей тело сверху.
 находится по формуле
находится по формуле

