Предельные теоремы и закон больших чисел

Все законы теории вероятностей получены из практики, то есть из наблюдений за массовыми случайными явлениями. Массовые случайные явления проявляются в статистической совокупности. Было замечено, что при определенных условиях массовые случайные явления порождают величину неслучайную, которая подчиняется вполне определенным закономерностям. Все полученные соответствующие теоремы и образуют теоремы закона больших чисел, в которых приведены условия, когда среднее значение случайных величин стремится к величине не случайной. Таким образом, закон больших чисел – это совокупность теорем, в которых приведены условия, при которых последовательность случайных величин подчиняется определенным закономерностям, то есть стремится к величине неслучайной.

Неравенство Чебышева: Вероятность того, что случайная величина Х отклоняется от своего математического ожидания на величину не меньше 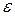, ограничена сверху величиной , где 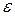– положительное действительное число:

или . (8.1)

В частности, если и существует М (Х), то

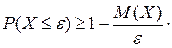или (8.2)

Если существует М (Х ²), то при любом справедливо неравенство:

. (8.3)

Теорема Чебышева (закон больших чисел): Если Х ₁, Х ₂,... последовательность независимых случайных величин, которые имеют конечные математические ожидания и ограниченные дисперсии (D (Х)< С), то при возрастании n среднее арифметическое наблюденных значений случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий:

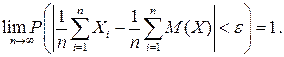
Отсюда следует, что для больших п справедливо неравенство:

Закон больших чисел справедлив и для зависимых случайных величин, то есть справедлива теорема Маркова:

Если для случайных величин Х ₁, Х ₂,... выполняется условие , то при возрастании п среднее арифметическое наблюденных значений случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий: .

Теорема Бернулли: Если производится п испытаний, в каждом из которых некоторое событие А может появиться с вероятностью р, то относительная частота появления события в п испытаниях сходится по вероятности к вероятности появления события в каждом испытании:

В частности для больших п

Теорема Пуассона: Пусть производится п независимых испытаний, в каждом их которых событие А появляется с вероятностями р ₁, р₂,…, p_n. Тогда при неограниченном увеличении числа испытаний относительная частота появления события А сходится по вероятности к среднему арифметическому вероятностей появления события в различных испытаниях:

Теорема Линдеберга-Леви: Пусть Х ₁, Х ₂,... независимые одинаково распределенные случайные величины с математическими ожиданиями т и дисперсиями σ ^2, то при неограниченном увеличении п, закон распределения нормированной случайной величины Z_n стремится к нормальному закону распределения с плотностью распределения вероятностей равной для которого m =0, σ = 1, где – нормированная случайная величина.

Это центральная предельная теорема для одинаково распределенных независимых случайных величин.

Теорема Ляпунова: Если Х ₁, Х ₂,... независимые случайные величины, имеющие конечные математические ожидания т, дисперсии σ ² и конечные абсолютные центральные моменты третьего порядка, удовлетворяющие условиям: , то закон распределения величины Z_n сходится к нормальному закону распределения с плотностью распределения вероятностей , для которого m =0, σ =1.

Эта теорема имеет большое практическое значение, так как, используя ее, можно вычислить вероятность того, что сумма независимых случайных величин принимает значение, принадлежащее интервалу. Условие , характеризует тот факт, что все случайные величины сравнимы между собой, то есть ни одна из случайных величин не имеет преимущества перед другими случайными величинами.

Рассмотрим дискретную случайную величину Х, которая характеризует число появлений события А в п независимых испытаниях. Эту случайную величину можно представить в виде суммы случайной величины X_i, каждая из которых характеризует число появлений события А в i- ом испытании:

Нормированная сумма случайных величин X_i, будет иметь вид: , где m – число появлений события А в испытаниях; р – вероятность появления события А в каждом испытании; n – число испытаний; q =1– p.

Если случайная величина Х подчиняется биномиальному закону распределения, то вычисление вероятности того, что некоторое событие А появиться т раз в п испытаниях по формуле Бернулли затруднительно, если п достаточно большое, а р мало. В этом случае можно воспользоваться следующими теоремами:

Теорема Муавра-Лапласа (локальная): Пусть производится п испытаний, в каждом из которых некоторое событие А может появиться с вероятностью р (0 <р<). Тогда для всех т, удовлетворяющих условию (где а, b – произвольные числа) выполняется соотношение:

Локальная теорема используется при больших значениях п для вычисления вероятности Р (А) того, что некоторое событие А наступает т раз в п испытаниях по формуле:

(8.4)

Теорема Маувра-Лаплаcа (интегральная): Пусть производится п независимых испытаний, в каждом из которых событие А может появиться с вероятностью p. Тогда для любых а и b справедливо соотношение:

Из предельного равенства теоремы следует формула:

(8.5)

X_i – число появлений события А в i -ом испытании.

Используя теорему Муавра-Лапласа, вычисляется вероятность неравенства т.е. справедлива формула:

(8.6)

(8.7)

В отличие от теорем Бернулли и Пуассона последние две формулы дают более точную оценку вероятности отклонений частоты появления событий от его математического ожидания и частости события от вероятности появления события в каждом испытании.

Задачи

8.1. Средний вес яблока весит 110г. Используя неравенство Чебышева, оценить вероятность того, что наудачу взятое яблоко весит не более 180г.

Решение. Случайная величина Х – вес случайно выбранного яблока. По условию задачи М (Х)=110. Тогда искомую вероятность оценим по второй формуле (8.2), где ε будет равно 180. Подставив значения М (Х)и ε, получим:

Ответ: .

8.2. Средняя скорость движения автомобилей на одном из участков автомобильной дороги равно 85 км/час. Используя неравенство Чебышева, оценить вероятность того, что у наудачу выбранного автомобиля его скорость не меньше 100 км/час.

Решение. Случайная величина Х – скорость наудачу выбранного автомобиля на данном участке автомобильной дороги. По условию задачи М (Х)=85 км/час. Искомую вероятность оценим, используя первую формулу (8.2), где ε =100 км/час. Подставив значения М (Х)=85 и ε =100, получим:

Ответ: р =0,85.

8.3. Средняя скорость ветра в одном из районов Земли15 км/час. Используя неравенство Чебышева, оценить вероятность того, что в наудачу выбранный день скорость ветра в этом районе будет не менее 100 км/час.

8.4. Для некоторого автопарка среднее число автобусов, отправляемых в
ремонт после месяца эксплуатации на городских линиях, равно 5. Оценить
вероятность события состоящего в том, что по истечении месяца в данном
автопарке будет отправлено в ремонт меньше 15 автобусов, если нет
информации о дисперсии.

8.5. Число фирм уклоняющихся от полной уплаты налогов для города N
является случайной величиной со средним значением 100 фирм и средним
квадратичным отклонением равным 20 фирмам. Оценить сверху вероятность
событий: А = { X ≥ 150}; В = { X > 200}.

8.6. Вероятность появления события А в каждом испытании равна 0,5.
Используя неравенство Чебышева оценить вероятность того, что число X появлений события А будет заключено в пределах от 40 до 60, если будет произведено 100 независимых испытаний.

Решение: X - число появлений события А в 100 независимых испытаниях. Найдем математическое ожидание М (Х)и дисперсию D (X):

M (X)= np =100×0,5=50; D (X) =npq =100×0,5×0,5=25.

Найдем максимальную разность между заданным числом появлений события и математическим ожиданием М (Х)=50: 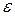=60–50=10. Воспользуемся неравенством Чебышева в форме:

Подставляя М (Х) = 50, D (X)=25, =10, получим:

.

Ответ: .

8.7. Вероятность появления события в каждом испытании равна 0,25. Используя неравенство Чебышева, оценить вероятность того, что число X появлений события заключено в пределах от 150 до 250, если будет произведено 800 испытаний.

8.8. Вероятность производства нестандартного изделия при данных технологических условиях равна 0,05. Оценить вероятность того, что число нестандартных изделий среди 1000 будет заключено в пределах от 85 до 95 включительно.

8.9. Дискретная случайная величина Х задана законом распределения:

 

xi
pi	0,2	0,1	0,4	0,3

 

Пользуясь неравенством Чебышева, оценить вероятность того, что случайная величина Х примет значение, удовлетворяющее неравенству .

Решение. Вычислим математическое ожидание и дисперсию случайной величины Х:

Воспользуемся неравенством Чебышева в форме:

Подставив значения 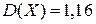и получим:

Ответ:

8.10. Дискретная случайная величина X задана законом распределения:

 

а)	xi	0,3	0,6	б)	xi	–2
pi	0,2	0,8	pi	0,2	0,1	0,3	0,15	0,25

 

Используя неравенство Чебышева, оценить вероятность того, что

а) б)

8.11. Заданы законы распределения попарно независимых случайных величин, образующих случайную последовательность{ Х_n }, n =1,2,3,…

 

а)

 

б)

 

в)

 

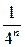
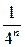
г)

 

Выяснить, применима ли к этим последовательностям теорема Чебышева?

Решение. а) Для того, чтобы к последовательности случайных величин была применима теорема Чебышева, достаточно, чтобы эти случайные величины были попарно независимы, имели конечные математические ожидания и равномерно ограниченные дисперсии.

По условию задачи случайные величины Х_n, n =1,2,3,…, попарно независимы, т.е. первое условие теоремы Чебышева выполнено.

Для проверки других условий вычислим математические ожидания и дисперсии этих случайных величин. Математические ожидания равны:

Значит, случайные величины Х_п имеет конечныематематические ожидания.

Для вычисления дисперсии составим законы распределения :

 

	n		n

 

Тогда дисперсии равны:

Следовательно, дисперсии заданных случайных величин равномерно ограничены числом 2, т.е. третье условие выполнено. Поскольку все требования выполняются, то к случайной последовательности { Х_n } теорема Чебышева применима.

8.12. Последовательность независимых случайных величин Х ₁, Х ₂,…, Х_п,… задана законом распределения

 

хi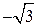
рi	1/3	1/3	1/3

 

Применима ли к данной последовательности теорема Чебышева?

8.13. При изготовлении деталей на станке-автомате брак составляет 2%. Найти вероятность того, что при проверке партии из 1000 деталей выявится отклонение от установленного процента брака меньше, чем на 1%.

Решение. Пусть событие А состоит в изготовлении бракованной детали. Вероятность его появления при каждом изготовлении (испытании) детали постоянна и равна 0,02, т.е. р =0,02. По условию задачи нам нужно установить, что относительная частота появления бракованной детали отклонится от вероятности появления бракованной детали в каждом испытании меньше, чем на 1%, т.е. меньше, чем на 0,01.

Воспользуемся теоремой Бернулли, т.е. неравенством

Поскольку п= 1000, ε= 0,01; р= 0,03, q= 1– р =1–0,02=0,98, то подставив эти значения, получим:

Таким образом, искомая вероятность Р ≥0,804.

8.14. Всхожесть семян некоторого растения составляет 80%. Найти вероятность того, что при посеве 10000 семян отклонение относительной частоты (доли) взошедших семян от вероятности того, что взойдет каждое из них, не превзойдет по модулю 0,03.

8.15. Для определения средней продолжительности жизни жителей некоторого города, численность которого равна 100000 человек, взяли на выборку по одному человеку из каждой тысячи. Известно, что для каждой тысячи жителей дисперсия не превышает 3,5 года. Оценить вероятность того, что отклонение средней выборочной продолжительности жизни отличается от средней продолжительности жизни жителей для всего города не более чем на 0,5 лет.

Решение. Введем случайные величины Х_i – продолжительность жизни i- го жителя города . Эти случайные величины независимы, имеют конечные математические ожидания и ограниченные дисперсии. Следовательно, для оценки искомой вероятности применим теорему Чебышева в форме:

Подставив значения ε =0,5; с =3,5 и п =100, определенные в условии задачи, получим

Ответ: Р >0,86.

8.16. Для определения средней продолжительности горения электроламп, изготовленных за некоторое время, в партии из 500 коробок было изъято по одной лампе из каждой коробки. Оценить вероятность того, что средняя продолжительность горения отобранных 500 ламп отличается от средней продолжительности горения во всей партии по модулю меньше, чем на 6 часов, если известно, что среднее квадратическое отклонение продолжительности горения ламп в каждой коробке меньше 3 часов.

8.17. На станке изготавливаются цилиндрические детали. Определить, сколько нужно произвести замеров, чтобы средний диаметр цилиндрической детали отличался от номинального значения m не более чем на 0,02 мм с вероятностью 0,98. Среднее квадратическое отклонение диаметров изготавливаемых цилиндрических деталей не превышает 0,03 мм и измерения производятся без погрешности.

Решение. Предположим, что выбор цилиндрической детали для замера диаметра, проводится наудачу. Тогда случайные величины Х_i – результаты измерения i -ой цилиндрической детали, являются независимыми случайными величинами. Они имеют конечные математические ожидания и ограниченные дисперсии, так как по условию задачи и, следовательно, Подставляя в неравенство значения с =0,0009 и ε =0,02, получаем

Поскольку то, решив это неравенство, найдем п:

Таким образом, поскольку п – натуральное число, то достаточно выполнить 113 замеров диаметров цилиндрических деталей.

Ответ: n =113.

8.18. Сколько раз нужно измерить данную величину, истинное значение которой равно т, чтобы с вероятностью, не меньшей, чем 0,95, можно было утверждать, что среднее арифметической этих измерений отличается от т по модулю меньше, чем на 2, если среднее квадратическое отклонение каждого измерения меньше 5.

8.19. При каких значениях п и р биномиальный закон распределения вероятностей аппроксимируется пуассоновским? При каких условиях из биномиального и пуассоновского распределений получаем нормальное распределение?

8.20. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена 75 раз.

Решение: Рассмотрим случайную величину, характеризующую число поражений мишени при 100 выстрелах: где Х_i – число поражений мишени при одном выстреле.

Так как п велико, воспользуемся локальной теоремой Лапласа (формулой (8.4)):

Определяем значение х:

По таблице функции найдем . Подставив значения n =100, p =0,8, q =1–0,8=0,2, в формулу (8.4), найдем искомую вероятность: .

Ответ: .

8.21. Найти вероятность того, что событие А наступит 1400 раз в 2400
испытаниях, если вероятность появления этого события в каждом
испытании равно 0,6.

8.22. Вероятность рождения мальчика равна 0,512. Найти вероятность того, что среди 100 новорожденных окажется: 1) 50 мальчиков; 2) больше мальчиков, чем девочек.

8.23. Вероятность появления события А в каждом из 2100 независимых испытаний равна 0,7. Найти вероятность того, что событие появится: а) не менее 1470 и более 1500 раз; б) не менее 1470 раз; в) не более 1496 раз.

Решение. а) Рассмотрим случайную величину Х ₂ – число появлений события А в 2100 испытаниях, которая равна 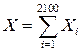, где Х_i – число появлений события А в i -ом испытании. Случайные величины Х_i имеют одинаковые математические ожидания и дисперсии Следовательно, для вычисления искомой вероятности можно применить интегральную теорему Муавра-Лапласа, т.е. формулу (8.5).

По условию задачи п =2100, т ₁=1470, т ₂=1500, р =0,7, q =1– р =0,3. Находим вначале и

По таблице значений функции Ф ^*(х), находим Ф ^*(0)=0,5 и Ф ^*(1,43)=0,9236. Затем по формуле (8.5) находим искомую вероятность:

Р ₂₁₀₀(1470;1500)= Ф ^*(1,43)– Ф ^*(0)=0,9236–0,5=0,4236.

Ответ: Р ₂₁₀₀(1470;1500)= 0,4236.

8.24. Проводятся последовательные испытания по схеме Бернулли. Вероятность осуществления события А в одном испытании равна 0,6. Считая
применимыми предельные теоремы Муавра-Лапласа, вычислить вероятность
следующих событий: В ={событие А произойдет в большинстве из 60 испытаний}; С ={число успешных осуществлений событий А в 60 испытаниях будет заключено между 30 и 42}.

8.25. Вероятность того, что деталь стандарта, равна 0,9. Случайная величина Х – число стандартных деталей. Сколько нужно проверить деталей, чтобы с вероятностью 0,95 можно было ожидать, что не менее 150 деталей будут стандартными.

Решение. Случайная величина где Х_i – число появлений события А в i -ом испытании; А ={при проверке оказалось, что деталь стандартна}; ; .

Воспользуемся формулой (8.5). Согласно условия задачи р =0,9, q =1– p =1–0,9=0,1, m ₁₌150, m ₂ =n – неизвестная величина, которую нужно определить. Подставив эти значения в (8.5), получим:

,

или , или .

Из условия задачи следует, что n >150, поэтому Поскольку Ф^*(х) – функция возрастающая и Ф^*(3,9)=1,0, то можно положить . Следовательно,

По таблице значений функции Ф^*(х) находим Ф(–1,645)=0,05. Тогда, сравнивая аргументы, получим:

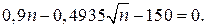
Решая полученное квадратное уравнение относительно , находим значение п: ; п =174 (с учетом того, что п – натуральное число).

Ответ: n =174.

8.26. Вероятность появления события в каждом из независимых испытаний равна 0,8. Сколько нужно произвести испытаний, чтобы с вероятностью 0,9 можно было ожидать, что событие появится не менее 75 раз?

8.27. Вероятность появления положительного результата в каждом из п опытов равна 0,9. Сколько нужно произвести опытов, чтобы с вероятностью 0,98 можно было ожидать, что не менее 150 опытов дадут положительный результат?

8.28. Отдел технического контроля проверил качество наудачу отобранных 900 деталей. Вероятность р того, что деталь стандартна равна 0,9. Случайная величина X – число стандартных деталей в партии. Найти наименьший интервал симметричный относительно М (Х), в котором с вероятностью, не
меньше 0,9544 будет заключено число стандартных деталей.

Решение. Воспользуемся формулой (8.7):

в которую подставим значения n =900; p =0,9; q =1– p =1–0,9=0,1; P =0,9544 из условия задачи. Получим равенство:

По таблице значений функции Ф ^*(х) находим Ф ^*(2)=0,9772. Сравнивая аргументы, получим , откуда .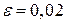

Возвращаясь к формуле (8.7), запишем неравенство 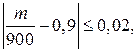решая которое, находим интервал, в котором заключено число стандартных деталей:

Ответ: [792; 829].

8.29. Обследуются 500 пар обуви изготовленной на предприятии, где брак составляет 2%. Случайная величина Х – число пар обуви, не содержащей брак. Найти наименьший интервал, в котором с вероятностью 0,99 будет заключено обследованное число пар обуви, не содержащей брак.

8.30. Ежедневно в городе N автобусами перевозится 500000 пассажиров, 10% из которых не оплачивает проезд. Случайная величина Х – число пассажиров, не оплативших проезд. Найти интервал, в котором с вероятностью 0,95 будет заключено число пассажиров, не оплативших проезд.

8.31. Отдел технического контроля проверяет вес 500 коробок с шоколадными конфетами. Их масса должна ровняться 1 кг.Известно, что масса 5% коробок не соответствует стандарту. Найти такое положительное число 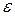, чтобы с вероятностью 0,95 модуль отклонения частости появления коробки с массой, не соответствующей стандарту, от его вероятности р =0,05 не превышая .

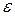8.32. В страховой компании застраховано 10000 автомобилей. Вероятность поломки любого автомобиля в результате аварии равна 0,006. Каждый
владелец застрахованного автомобиля платит в год 120 ден.ед. страховых
взносов и в случае поломки автомобиля в результате аварии получает от
компании 3000 ден.ед. Найти вероятность того, что: 1) A ={по истечении года
работы страховая компания потерпит убытки}, 2) B ={страховая компания получит прибыль не менее К ден.ед.}, если К =30000; 40000; 50000.

Решение. 1) Страховая компания потерпит убыток, если придется выплатить потерпевшим сумму, большую страховых взносов (сумма страховых взносов равна 120·10000=1200000). Сумма выплат определяется числом автомобилей m, попавших в аварию и равна . Пусть случайная величина Х – число автомобилей, попавших в аварию. Введем обозначения: M – предельное число автомобилей, попавших в аварию; S – сумма, выплачиваемая пострадавшему; с – страховой взнос; n – количество застрахованных автомобилей.

Страховая компания потерпит убыток, если 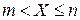. Тогда, воспользовавшись формулой (8.5), определим вероятность события А:

.

Подставив данные из условия задачи и значение m, вычисленное из равенства ; , получим

Ответ: 1) Р =0.

8.33. С конвейера сходит 85% автомобилей, не содержащих неисправностей. Сколько автомобилей следует проверить, чтобы с вероятностью 0,997 отклонение частости исправных автомобилей среди сошедших с конвейера от вероятности р =0,85 того, что случайно выбранный автомобиль исправен, по модулю не превосходило 0,01?

8.34. Всхожесть семян моркови равна 0,95. Найти вероятность того, что из 1000 посаженных семян моркови число проросших заключено межу 870 и 920.

8.35. Определить, сколько нужно произвести замеров поперечного сечения сосен, предназначенных для вырубки, на большом участке, чтобы средний диаметр сосен отличался от заданного m не более чем на 4 см с вероятностью не меньшей 0,95. Среднее квадратическое отклонение поперечного сечения сосен на данном участке не превышает 9 см и измерения проводятся без погрешности.

8.36. Столовая, вмещающая 850 человек, имеет два разных входа. Около каждого из входов имеется свой гардероб. Сколько мест должно быть в каждом из гардеробов, для того, чтобы в среднем в 95 случаях из 100 все посетители
могли раздеться в гардеробе того входа, через который они вошли?
Предполагается, что посетители приходят парами, и каждая пара независимо
от других выбирает с вероятностью 0,5 любой из входов. Насколько можно
будет сократить число мест в гардеробе, если посетители будут приходить
по одиночке и также независимо друг от друга с равной вероятностью
выбирать любой из входов.

8.37. Известно, что в среднем 7% студентов носят очки. Какова вероятность того, что из 250 студентов некоторого факультета окажется не менее 10% носящих очки?

8.38. Оценить вероятность события: .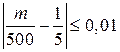

8.39. Среднее число вызовов на АТС за 1 минуту равно , где случайная величина Х – число вызовов, поступивших на АТС. Какова вероятность событий: ; ?

8.40. В ящике содержатся изделия, изготовленные на двух заводах в отношении 3:2. Проводятся последовательные извлечения одного изделия с возвращением, причем каждый раз фиксируется на каком заводе изготовлено изделие. Каково минимальное число извлечений, при котором с вероятностью не меньшей 0,9948 можно ожидать, что отклонение относительной частоты появления изделия завода №1 от вероятности его появления в одном извлечении не превысит величины ?