Важную роль в процессе обработки данных (поимо самих данных, подвергаемых обработке) играет активная составляющая процесса - некоторая сущность, выполняющая обработку. Таким обработчиком, или преобразователем данных, могут быть как люди, так и некоторые устройства. Важнейшие характеристики процесса обработки данных зависят от того, как функционирует преобразователь. Поэтому создание и исследование различных моделей обработки имеет важное теоретическое и практическое значение. Одной из таких моделей является понятие конечного автомата [32], [36]. Конечный автомат можно охарактеризовать как устройство, имеющее входной и выходной каналы; в процессе функционирования на каналы поступают дискретные порции данных (буквы алфавита). Автомат может находиться в одном из конечного числа внутренних состояний. По определенному закону (в зависимости от состояния автомата и входных данных) осуществляется преобразование входной порции данных в выходные данные и смена состояния автомата. Формально конечный автомат определяется следующим образом.
Определение. Конечным автоматом называется набор из пяти объектов 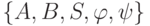 , в котором:
, в котором:
· 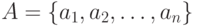 - входной алфавит;
- входной алфавит;
· 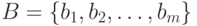 - выходной алфавит);
- выходной алфавит);
· 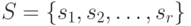 - множество внутренних состояний автомата;
- множество внутренних состояний автомата;
· 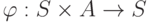 - функция перехода в следующее состояние (переходная функция);
- функция перехода в следующее состояние (переходная функция);
·  - функция выхода (выходная функция).
- функция выхода (выходная функция).
Таким образом, конечный автомат математически описывается тремя множествами и двумя функциями. Функционирование автомата состоит в том, что он "считывает" последовательность входных символов ("программу") и затем "выпечатывает" последовательность выходных символов. Действие происходит последовательно. Конечный автомат, находящийся сначала во внутреннем состоянии 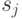 , считывает первый входной символ
, считывает первый входной символ  . Функция
. Функция 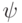 принимает на паре
принимает на паре  значение
значение 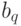 , которое выпечатывается в качестве первого выходного символа. Функция
, которое выпечатывается в качестве первого выходного символа. Функция  принимает на паре
принимает на паре  значение
значение 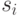 , которое является следующим внутренним состоянием автомата. Затем автомат считывает новый входной символ, выпечатывает выходной, переходит в следующее состояние и т.д., пока не кончится программа.
, которое является следующим внутренним состоянием автомата. Затем автомат считывает новый входной символ, выпечатывает выходной, переходит в следующее состояние и т.д., пока не кончится программа.
На рис.8.1 дан удобный способ представления последовательных тактов работы автомата.
Будем предполагать, что программа записана на входной ленте. Автомат считывает с нее входные знаки один за другим. По прочтении каждого входного знака выпечатывается выходной знак на выходной ленте, и автомат переходит в следующее состояние прежде чем считать следующий символ программы. Позже мы введем другие способы представления: графы и таблицы состояний.
В нашем определении подразумевается, что функции  и
и 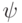 в описа-нии автомата
в описа-нии автомата  всюду определены: каждый элемент
всюду определены: каждый элемент  задает их значения. Такое описание автомата является полным. Коль скоро задано начальное состояние такого автомата, он способен считывать любую программу и выдавать однозначно определенную цепочку символов. Иными словами, существует функция, которая ставит в соответствие любому начальному состоянию
задает их значения. Такое описание автомата является полным. Коль скоро задано начальное состояние такого автомата, он способен считывать любую программу и выдавать однозначно определенную цепочку символов. Иными словами, существует функция, которая ставит в соответствие любому начальному состоянию  и любой последовательности входных символов вполне определенную последовательность выходных символов.
и любой последовательности входных символов вполне определенную последовательность выходных символов.

Рис. 8.1. Конечный автомат
Пусть 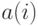 - полученный на вход автомата знак на
- полученный на вход автомата знак на  -м шаге,
-м шаге, 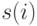 - состояние, в котором находился автомат на
- состояние, в котором находился автомат на  -м шаге, а
-м шаге, а 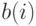 - знак, который вырабатывает автомат на
- знак, который вырабатывает автомат на  -м шаге в качестве выходного значения. Работа автомата, то есть переход из состояния в состояние и появление выходных знаков, с использованием функций
-м шаге в качестве выходного значения. Работа автомата, то есть переход из состояния в состояние и появление выходных знаков, с использованием функций  и
и 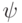 может быть описано выражениями
может быть описано выражениями
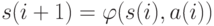
| (8.1)
|

| (8.2)
|
Поскольку множества 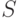 и
и 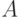 конечны, функции, заданные на их декартовом произведении
конечны, функции, заданные на их декартовом произведении 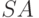 , удобно задавать табличным способом. На рис.8.2 показан общий вид таблиц, задающих переходную функцию
, удобно задавать табличным способом. На рис.8.2 показан общий вид таблиц, задающих переходную функцию  и выходную функцию
и выходную функцию 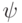 конечного автомата.
конечного автомата.
Рассмотрим пример конечного автомата, у которого 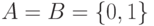 , имеется два состояния
, имеется два состояния  , а функции
, а функции  и
и 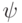 задаются таблицами
задаются таблицами
Пусть на вход автомата подается последовательность знаков (слово) 1,0,0,1,1,0,1 или в более короткой записи 1001101. Проследим, как меняется состояние автомата в процессе обработки этого слова и какая после-довательность знаков формируется на выходе. Для этого рассмотрим таблицу, состоящую из трех строк. В первой строке записаны знаки, поступающие на вход автомата. Во второй строке записываются состояния, в которых оказывается автомат в процессе обработки входного слова. Наконец, в третьей строке записываются знаки, которые появляются на выходе автомата в результате его работы.

Рис. 8.2. Табличное задание переходной и выходной функций
Обработка входной последовательности знаков производится по шагам. На каждом шаге обрабатывается один знак. В таблице каждому шагу обработки соответствует один столбец. Пусть в момент поступления первого знака, которым является 1, автомат находился в состоянии 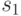 . Тогда в
. Тогда в 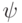 на выходе появится знак 0, а в соответствии с определением функции
на выходе появится знак 0, а в соответствии с определением функции  автомат перейдет в состояние
автомат перейдет в состояние 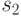 , которое записывается во вторую строку следующего (второго) столбца таблицы. При поступлении второго знака обрабатываемого слова получим
, которое записывается во вторую строку следующего (второго) столбца таблицы. При поступлении второго знака обрабатываемого слова получим 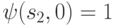 (записывается в третью строку второго столбца таблицы) и
(записывается в третью строку второго столбца таблицы) и 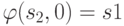 (записывается во вторую строку следующего (третьего) столбца таблицы). Процесс обработки следующих знаков происходит аналогичным образом и завершает-ся после обработки последнего знака. В результате исходное слово 1001101 преобразуется в слово 0100110, которое, как можно заметить, является "сдвигом" исходного слова, то есть получается удалением последнего знака из исходного слова и добавлением знака "0" в начало исходного слова.
(записывается во вторую строку следующего (третьего) столбца таблицы). Процесс обработки следующих знаков происходит аналогичным образом и завершает-ся после обработки последнего знака. В результате исходное слово 1001101 преобразуется в слово 0100110, которое, как можно заметить, является "сдвигом" исходного слова, то есть получается удалением последнего знака из исходного слова и добавлением знака "0" в начало исходного слова.
Помимо рассмотренного табличного способа существует еще графический способ описания (задания) конечных автоматов в виде помеченного ориентированного графа, который называется "диаграмма состояний". Вершины этого графа помечены символами, обозначающими внутренние состояния. Каждое ребро помечено парой символов  , где
, где 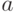 - входной знак, который вызывает переход в следующее состояние, отвечающее этому ребру, а
- входной знак, который вызывает переход в следующее состояние, отвечающее этому ребру, а  - выходной знак, который автомат выдает в результате обработки входного знака. Из каждой вершины диаграммы выходит столько дуг, сколько знаков имеется во входном алфавите.
- выходной знак, который автомат выдает в результате обработки входного знака. Из каждой вершины диаграммы выходит столько дуг, сколько знаков имеется во входном алфавите.

Рис. 8.3. Диаграмма состояний сдвигающего автомата
Диаграмма состояний рассмотренного автомата, сдвигающего вправо на один знак входное слово, показана на рис.8.3.
Табличный и графический способы описания конечных автоматов дополняют друг друга. Использование таблиц удобнее для вычислений, а диаграммы более наглядны.
Пусть 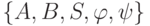 - некоторый автомат. Выделим одно состояние, которое назовем начальным и с которого будет начинаться обработка всех входящих слов. Тогда любой входной строке
- некоторый автомат. Выделим одно состояние, которое назовем начальным и с которого будет начинаться обработка всех входящих слов. Тогда любой входной строке  длины
длины  , где
, где 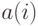 - знак на
- знак на  -м месте входной последовательности, однозначно соответствует строка внутренних состояний,
-м месте входной последовательности, однозначно соответствует строка внутренних состояний, 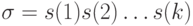 , длины
, длины  , где
, где 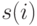 - состояние после
- состояние после  -го шага работы, которая получается последовательным применением отображения
-го шага работы, которая получается последовательным применением отображения  по формуле (8.1). Аналогично выходная строка
по формуле (8.1). Аналогично выходная строка 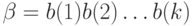 длины
длины  , где
, где 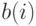 - знак на
- знак на  -м месте выходной последовательности, однозначно определится последовательным применением отображения
-м месте выходной последовательности, однозначно определится последовательным применением отображения  по формуле (8.2).
по формуле (8.2).
Таким образом, автомат можно рассматривать как устройство, преобразующее для заданного начального состояния  входную строку
входную строку 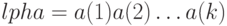 в строку
в строку 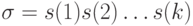 и выходную строку
и выходную строку 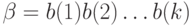 и тем самым реализующее функции (преобразования)
и тем самым реализующее функции (преобразования) 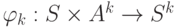 и
и 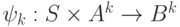 , которые рекурсивно строятся по функциям
, которые рекурсивно строятся по функциям  и
и 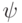 .
.





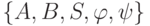 , в котором:
, в котором: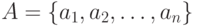 - входной алфавит;
- входной алфавит;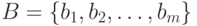 - выходной алфавит);
- выходной алфавит);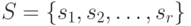 - множество внутренних состояний автомата;
- множество внутренних состояний автомата;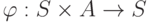 - функция перехода в следующее состояние (переходная функция);
- функция перехода в следующее состояние (переходная функция); - функция выхода (выходная функция).
- функция выхода (выходная функция).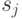 , считывает первый входной символ
, считывает первый входной символ  . Функция
. Функция 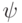 принимает на паре
принимает на паре  значение
значение 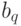 , которое выпечатывается в качестве первого выходного символа. Функция
, которое выпечатывается в качестве первого выходного символа. Функция  принимает на паре
принимает на паре 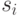 , которое является следующим внутренним состоянием автомата. Затем автомат считывает новый входной символ, выпечатывает выходной, переходит в следующее состояние и т.д., пока не кончится программа.
, которое является следующим внутренним состоянием автомата. Затем автомат считывает новый входной символ, выпечатывает выходной, переходит в следующее состояние и т.д., пока не кончится программа. всюду определены: каждый элемент
всюду определены: каждый элемент  задает их значения. Такое описание автомата является полным. Коль скоро задано начальное состояние такого автомата, он способен считывать любую программу и выдавать однозначно определенную цепочку символов. Иными словами, существует функция, которая ставит в соответствие любому начальному состоянию
задает их значения. Такое описание автомата является полным. Коль скоро задано начальное состояние такого автомата, он способен считывать любую программу и выдавать однозначно определенную цепочку символов. Иными словами, существует функция, которая ставит в соответствие любому начальному состоянию  и любой последовательности входных символов вполне определенную последовательность выходных символов.
и любой последовательности входных символов вполне определенную последовательность выходных символов.
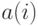 - полученный на вход автомата знак на
- полученный на вход автомата знак на  -м шаге,
-м шаге, 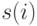 - состояние, в котором находился автомат на
- состояние, в котором находился автомат на 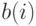 - знак, который вырабатывает автомат на
- знак, который вырабатывает автомат на 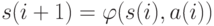

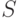 и
и 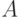 конечны, функции, заданные на их декартовом произведении
конечны, функции, заданные на их декартовом произведении 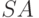 , удобно задавать табличным способом. На рис.8.2 показан общий вид таблиц, задающих переходную функцию
, удобно задавать табличным способом. На рис.8.2 показан общий вид таблиц, задающих переходную функцию 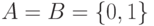 , имеется два состояния
, имеется два состояния  , а функции
, а функции 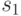
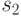

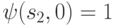 (записывается в третью строку второго столбца таблицы) и
(записывается в третью строку второго столбца таблицы) и 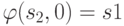 (записывается во вторую строку следующего (третьего) столбца таблицы). Процесс обработки следующих знаков происходит аналогичным образом и завершает-ся после обработки последнего знака. В результате исходное слово 1001101 преобразуется в слово 0100110, которое, как можно заметить, является "сдвигом" исходного слова, то есть получается удалением последнего знака из исходного слова и добавлением знака "0" в начало исходного слова.
(записывается во вторую строку следующего (третьего) столбца таблицы). Процесс обработки следующих знаков происходит аналогичным образом и завершает-ся после обработки последнего знака. В результате исходное слово 1001101 преобразуется в слово 0100110, которое, как можно заметить, является "сдвигом" исходного слова, то есть получается удалением последнего знака из исходного слова и добавлением знака "0" в начало исходного слова. , где
, где 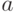 - входной знак, который вызывает переход в следующее состояние, отвечающее этому ребру, а
- входной знак, который вызывает переход в следующее состояние, отвечающее этому ребру, а  - выходной знак, который автомат выдает в результате обработки входного знака. Из каждой вершины диаграммы выходит столько дуг, сколько знаков имеется во входном алфавите.
- выходной знак, который автомат выдает в результате обработки входного знака. Из каждой вершины диаграммы выходит столько дуг, сколько знаков имеется во входном алфавите.
 длины
длины  , где
, где 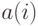 - знак на
- знак на 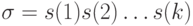 , длины
, длины 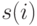 - состояние после
- состояние после 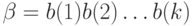 длины
длины  входную строку
входную строку 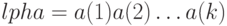 в строку
в строку 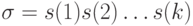 и выходную строку
и выходную строку 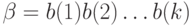 и тем самым реализующее функции (преобразования)
и тем самым реализующее функции (преобразования) 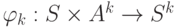 и
и 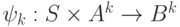 , которые рекурсивно строятся по функциям
, которые рекурсивно строятся по функциям 


