Смещение точек снимка
На снимке равнинной местности (рис. 2, плоскость Е), полученном при отвесном положении оптической оси съемочной камеры, элементы ситуации изобразятся без искажений. Сетка квадратов на местности, напр., изобразится на снимке 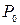 подобной сеткой в масштабе:
подобной сеткой в масштабе: 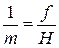
Рис. 2. Горизонтальный снимок равнинной местности
Наклон камеры на некоторый угол аР нарушит подобие — изображение сетки квадратов перспективно преобразуется (рис. 3). На рис. 4 показаны: в позитивном варианте горизонтальный снимок Р0 и наклонный снимок Р, а также равнинная местность Е в сечении их плоскостью главного вертикала. Снимки Ро и Р пересекутся по горизонтали hchc, так как oS= 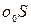 =f. В прямоугольных треугольниках
=f. В прямоугольных треугольниках 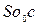 и
и 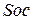 общая гипотенуза и равные катеты; следовательно, эти треугольники равны; поэтому Sc — биссектриса угла аР a точка с лежит на hchc.
общая гипотенуза и равные катеты; следовательно, эти треугольники равны; поэтому Sc — биссектриса угла аР a точка с лежит на hchc.
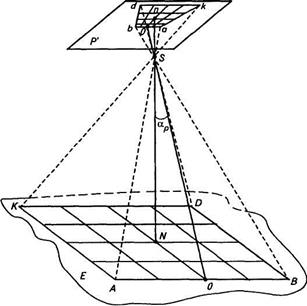
Рис. 3. Наклонный снимок равнинной местности
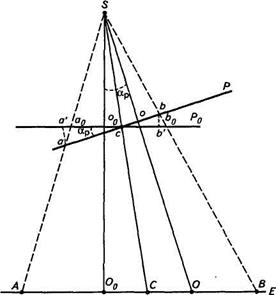
Рис. 4. Смещение точек снимка вследствие его наклона
Произвольно выбранные на снимке точки а и b, изобразятся на снимке Ро точками а0 и bо. Приняв за начало отсчетов общую для обоих снимков точку с, отложим на снимке Ро отрезки 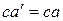 и
и 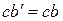 . В результате получим размеры смещения изображения точек А и В соответственно
. В результате получим размеры смещения изображения точек А и В соответственно 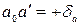 и
и 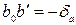 .
.
Значение δа для точек, расположенных не на главной вертикали, будет зависеть также от угла φ, отсчитываемого от положительного направления главной вертикали до направления, исходящего из точки с на анализируемую точку, например на точку а (рис.5), против хода часовой стрелки.
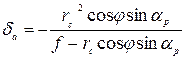 (2)
(2)
где rс — отстояние определяемой точки снимка от точки нулевых искажений.
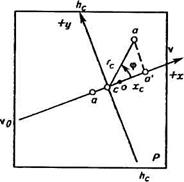
Рис.5 Правило измерения углов φ при определении смещения точек снимка вследствие его наклона
Анализ формулы показывает:
· смещения 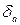 ,возрастают при увеличении угла
,возрастают при увеличении угла 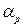 и уменьшении фокусного расстояния съемочной камеры;
и уменьшении фокусного расстояния съемочной камеры;
· точки, расположенные на горизонтали hchc, не смещаются;
· максимальные смещения точек при определенном значении rс будут в точках, располагающихся на главной вертикали (cosφ = ±l);
· точки, расположенные от горизонтали hchc в сторону положительных абсцисс, смещаются к точке с, а в сторону отрицательных абсцисс — от точки с (на рис.6 a0, b0, d0, e0 — положение точек на горизонтальном снимке).
При использовании снимков плановой съемки (а < 3°) можно применять упрощенные формулы:
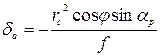 или
или 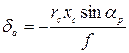 (3)
(3)
так как выражение 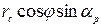 имеет существенно меньшее значение в сравнении с величиной f. В формуле
имеет существенно меньшее значение в сравнении с величиной f. В формуле 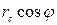 выражены через хс — абсциссу точки в системе координат vov — ось х, hchc — ось у (рис. 5).
выражены через хс — абсциссу точки в системе координат vov — ось х, hchc — ось у (рис. 5).
Изменение масштаба снимка
Различие по величине смещения точек за влияние угла наклона снимка обусловливает непостоянство масштаба по полю кадра. Ранее отмечалось, что точки, расположенные на линии hchc, за влияние наклона не смещаются. Очевидно, масштаб по этой линии будет постоянным и равным масштабу горизонтального снимка:
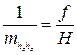 (4)
(4)
Горизонталь hchc называют линией неискаженных масштабов. На прочих горизонталях масштаб также будет постоянным, но на каждой горизонтали свой. Его выражают формулой:
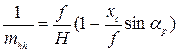 (5)
(5)
в которой хс — абсцисса горизонтали при начале координат в точке с. Масштаб вдоль главной вертикали определяют по формуле:
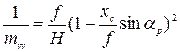 (6)
(6)
Масштаб по произвольному радиальному направлению может быть вычислен по формуле:
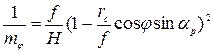 (7)
(7)
В результате анализа формул 5 и 7 можно установить:
· масштаб по главной вертикали изменяется быстрее, чем последовательно по горизонталям;
· в точке с масштаб бесконечно малого отрезка по вертикали и любому другому направлению равен масштабу в той же точке по горизонтали. Этот масштаб называют главным;
· масштаб в части снимка с положительными абсциссами мельче, а в части с отрицательными абсциссами крупнее главного.
Используя формулы, можно решить ряд практических задач, например определить возможности выполнения метрических действий непосредственно по снимку равнины с помощью его среднего масштаба. Такая задача может возникнуть, например, при нанесении промерами на снимок не изобразившихся по тем или иным причинам объектов (досъемка при дешифрировании). При создании кадастровых планов и карт досъемочные работы выполняют с использованием линейных промеров длиной 15... 25 мм на снимке. Средняя абсолютная погрешность измерения линий на снимке в полевых условиях — 0,15...0,20 мм. Средняя относительная погрешность при этом будет примерно 1/100. Погрешность за разномасштабность, обусловленная наклоном снимка, должна быть примерно той же и точнее.
Ранее установлено, что наиболее интенсивно масштаб снимка изменяется вдоль главной вертикали. Поэтому допустимость выполнения метрических действий непосредственно по снимку равнины должна определяться именно по этому направлению. Критерием допустимости может быть среднее относительное отклонение знаменателя масштаба изображения вдоль главной вертикали (mvv) от знаменателя главного масштаба снимка (m):
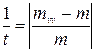
Аэрофотосъемку в целях создания кадастровых планов и карт выполняют преимущественно с использованием гиростабилизированных АФУ. Поэтому в большинстве случаев метрические действия непосредственно на снимках равнины можно выполнять с использованием единого главного масштаба, определяемого по известным значениям/и Н, с помощью измерений в натуре базисов или по координатам опознанных на снимках точек геодезической опоры.
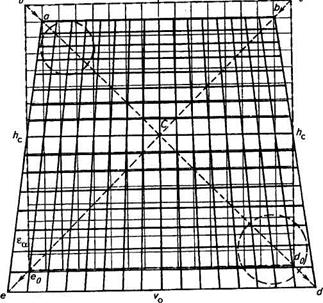
Для поиска путей решения той же задачи при недостаточной точности использования среднего масштаба рассмотрим рисунок 8.7, на котором тонкими линиями показана сетка квадратов (прообраз) с поворотными пунктами общей границы ао, b$, do и /0, а также преобразованное за наклон снимка изображение прообраза. Поворотными пунктами последнего будут a, b, du I.
Для повышения наглядности характера преобразования в данном случае использован простейший вариант — главная вертикаль снимка vov проходит через центр сетки и совпадает с одним из направлений ее сторон. Квадраты при этом преобразуются в трапеции. В общем же случае — в четырехугольники более сложной конфигурации. Для иллюстрации этого утверждения воспользуемся репродукцией картины Н. Н. Ге (рис. 8.8), на которой квадратные элементы пола наблюдаются под значительным углом (в нашей терминологии — под углом съемки ар) случайного направления.
Вернемся к рисунку 8.7. При существенном изменении масштаба изображения квадратов в пределах всей сетки, например в зонах при точках avid (обозначены окружностями), в пределах каждой из этих зон разномасштабность существенно меньшая.
Рис. 7. Искажение сетки квадратов на плановом снимке при совпадении направления главной вертикали с направлением продольных сторон исходной сетки (прообраза)

Рис. 8. Иллюстрация перспективного искажения произвольно ориентированной сетки квадратов относительно направления главной вертикали
Следовательно, необходимая точность выполнения метрических действий непосредственно по снимку может быть достигнута путем использования отдельных масштабов для его разных зон — частных масштабов.
Искажение площадей
Непостоянство масштаба снимка равнины при 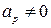 приведет к искажению площадей. Относительная ошибка определения площади выражается формулой, предложенной Н. Н. Веселовским:
приведет к искажению площадей. Относительная ошибка определения площади выражается формулой, предложенной Н. Н. Веселовским:
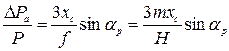
где хс — абсцисса центра измеряемого участка в принятой ранее системе координат.
Проанализируем приведенную формулу:
искажение площади уменьшается с увеличением f и с оответственным увеличением высоты съемки;
искажение уменьшается также с приближением участка к горизонтали hchc. Площади участков, центр которых расположен на горизонтали hchc, не искажаются.
Поскольку положение горизонтали обычно не известно, то это заключение имеет чисто теоретическое значение. Но в частном случае площади участков, центр которых совмещается с главной точкой (строго — с точкой с), за наклон снимка не искажаются.
Очевидно, искажения площадей участков за наклон снимка в определенных его частях будут близкими между собой и могут оказаться в пределах установленных норм. Это значит, что, используя частные масштабы зон, площади участков можно определять непосредственно по снимкам.
Искажение направлений
Наличие искажения направлений на наклонном снимке можно видеть на рисунке 7. Например, направление стороны сетки ае изменилось на 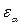 . Здесь можно выявить также строгую закономерность в распределении значений искажений по полю снимка. В данном частном случае (vov направлена вдоль стороны сетки) направления, перпендикулярные vov, не исказятся. Иллюстрацией искажения направлений в общем случае может служить также репродукция картины Н. Н. Ге (рис. 8).
. Здесь можно выявить также строгую закономерность в распределении значений искажений по полю снимка. В данном частном случае (vov направлена вдоль стороны сетки) направления, перпендикулярные vov, не исказятся. Иллюстрацией искажения направлений в общем случае может служить также репродукция картины Н. Н. Ге (рис. 8).
Определить искажения направления за наклон снимка можно с помощью рисунка 9. Исследуемое направление проходит через точки а и b (на рисунке показана правая верхняя часть снимка). Это направление пересечется с горизонталью hchc в точке к под углом 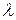 . Опустив на линию аb перпендикуляр, получим точку d. Угол, образованный направлениями перпендикуляра и главной вертикали, будет также равен А.. Введя в положение точки d поправку, определенную по формуле (2), найдем не смещенное за угол наклона снимка положение этой точки —
. Опустив на линию аb перпендикуляр, получим точку d. Угол, образованный направлениями перпендикуляра и главной вертикали, будет также равен А.. Введя в положение точки d поправку, определенную по формуле (2), найдем не смещенное за угол наклона снимка положение этой точки — 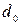 . Наклонный и горизонтальный снимок пересекаются по линии hchc. Это значит, что точка к принадлежит и неискаженному направлению, проходящему через точку
. Наклонный и горизонтальный снимок пересекаются по линии hchc. Это значит, что точка к принадлежит и неискаженному направлению, проходящему через точку 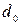 . Угол
. Угол 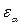 , образованный при этом, будет выражать значения искажения направления за наклон снимка.
, образованный при этом, будет выражать значения искажения направления за наклон снимка.
Рис. 9. Геометрическая интерпретация искажения направления на наклонном снимке
Вычислить 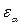 можно по формуле Я. И. Гебгарта:
можно по формуле Я. И. Гебгарта:
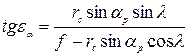
где  — кратчайшее расстояние от точки с до исследуемого направления.
— кратчайшее расстояние от точки с до исследуемого направления.
Положения точки с и главной вертикали обычно неизвестны. Поэтому полученную формулу применяют при определении возможности использования конкретных снимков для решения графических задач непосредственно по снимкам, вычисляя при этом предельные искажения. Для этого можно использовать упрощенную формулу при различных аргументах и фокусных расстояниях
5. Влияние рельефа местности на метрические свойства снимков
Смещение точек снимка
|
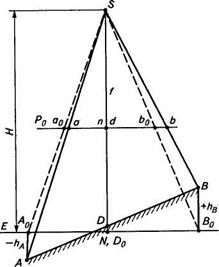
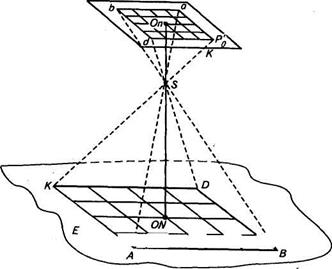
Сечение горизонтального снимка Ро и земной поверхности (с точками А, В и D) отвесной плоскостью, проходящей через центр проекции S, показано на рисунке 10. Эта плоскость пересечет снимок по линии, проходящей через точку надира п. Здесь же, в данном случае, располагаются точки о и с. Пересечем местность произвольной горизонтальной плоскостью Е. Точки А0 и Во — ортогональные проекции точек А и В на плоскость Е. Превышения точек А и В над плоскостью Е соответственно - hA и + hВ. На снимке точки местности и их ортогональные проекции на плоскость Е изобразятся соответственно точками а и b, a0 и bо. Заметим, что точка а, с отрицательным превышением, сместилась относительно точки а0 к точке надира, а точка b, с положительным превышением, — от точки надира. Величины aoa и bob — смещения точек а и b за влияние рельефа местности. Изображение точки местности D, лежащей на отвесном проектирующем луче, не сместится, независимо от ее превышения над плоскостью Е. Вывод: точки снимка за влияние рельефа местности смещаются по направлению к точке надира или от нее в зависимости от знака превышения.
Рис. 10. Смещение точек снимка вследствие влияния рельефа местности
Смещения точек за влияние рельефа местности определяют по формуле:
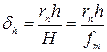
где 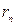 — отстояние определяемой точки на снимке от точки надира; h — превышение точки над горизонтальной плоскостью, принятой за исходную; H—высота съемки над той же плоскостью; т — знаменатель масштаба изображения, отнесенного к той же плоскости.
— отстояние определяемой точки на снимке от точки надира; h — превышение точки над горизонтальной плоскостью, принятой за исходную; H—высота съемки над той же плоскостью; т — знаменатель масштаба изображения, отнесенного к той же плоскости.





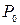 подобной сеткой в масштабе:
подобной сеткой в масштабе: 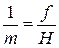
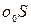 =f. В прямоугольных треугольниках
=f. В прямоугольных треугольниках 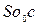 и
и 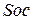 общая гипотенуза и равные катеты; следовательно, эти треугольники равны; поэтому Sc — биссектриса угла аР a точка с лежит на hchc.
общая гипотенуза и равные катеты; следовательно, эти треугольники равны; поэтому Sc — биссектриса угла аР a точка с лежит на hchc.

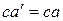 и
и 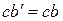 . В результате получим размеры смещения изображения точек А и В соответственно
. В результате получим размеры смещения изображения точек А и В соответственно 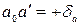 и
и 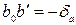 .
.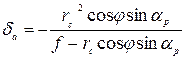 (2)
(2)
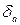 ,возрастают при увеличении угла
,возрастают при увеличении угла 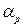 и уменьшении фокусного расстояния съемочной камеры;
и уменьшении фокусного расстояния съемочной камеры;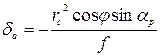 или
или 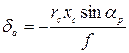 (3)
(3)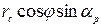 имеет существенно меньшее значение в сравнении с величиной f. В формуле
имеет существенно меньшее значение в сравнении с величиной f. В формуле 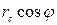 выражены через хс — абсциссу точки в системе координат vov — ось х, hchc — ось у (рис. 5).
выражены через хс — абсциссу точки в системе координат vov — ось х, hchc — ось у (рис. 5).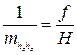 (4)
(4)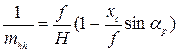 (5)
(5)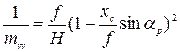 (6)
(6)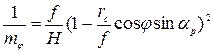 (7)
(7)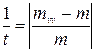

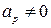 приведет к искажению площадей. Относительная ошибка определения площади выражается формулой, предложенной Н. Н. Веселовским:
приведет к искажению площадей. Относительная ошибка определения площади выражается формулой, предложенной Н. Н. Веселовским: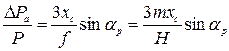
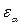 . Здесь можно выявить также строгую закономерность в распределении значений искажений по полю снимка. В данном частном случае (vov направлена вдоль стороны сетки) направления, перпендикулярные vov, не исказятся. Иллюстрацией искажения направлений в общем случае может служить также репродукция картины Н. Н. Ге (рис. 8).
. Здесь можно выявить также строгую закономерность в распределении значений искажений по полю снимка. В данном частном случае (vov направлена вдоль стороны сетки) направления, перпендикулярные vov, не исказятся. Иллюстрацией искажения направлений в общем случае может служить также репродукция картины Н. Н. Ге (рис. 8).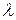 . Опустив на линию аb перпендикуляр, получим точку d. Угол, образованный направлениями перпендикуляра и главной вертикали, будет также равен А.. Введя в положение точки d поправку, определенную по формуле (2), найдем не смещенное за угол наклона снимка положение этой точки —
. Опустив на линию аb перпендикуляр, получим точку d. Угол, образованный направлениями перпендикуляра и главной вертикали, будет также равен А.. Введя в положение точки d поправку, определенную по формуле (2), найдем не смещенное за угол наклона снимка положение этой точки — 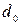 . Наклонный и горизонтальный снимок пересекаются по линии hchc. Это значит, что точка к принадлежит и неискаженному направлению, проходящему через точку
. Наклонный и горизонтальный снимок пересекаются по линии hchc. Это значит, что точка к принадлежит и неискаженному направлению, проходящему через точку 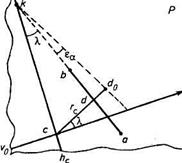
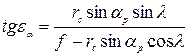
 — кратчайшее расстояние от точки с до исследуемого направления.
— кратчайшее расстояние от точки с до исследуемого направления.
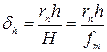
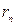 — отстояние определяемой точки на снимке от точки надира; h — превышение точки над горизонтальной плоскостью, принятой за исходную; H—высота съемки над той же плоскостью; т — знаменатель масштаба изображения, отнесенного к той же плоскости.
— отстояние определяемой точки на снимке от точки надира; h — превышение точки над горизонтальной плоскостью, принятой за исходную; H—высота съемки над той же плоскостью; т — знаменатель масштаба изображения, отнесенного к той же плоскости.


