1 Загрузить Mathcad. Сохранить новый документ с именем ФИОСтудента3.
2 Ввести в поле документа данные о студенте и выполняемой лабораторной работе.
3 Определить системную переменную ORIGIN равной единице.
4 Создать первым способом массивы: матрицы (имена A, B, D) размером 5×5 и векторы с1 и с2 размером 5×1 и 1×5 соответственно. Присвоить им произвольные значения. Вывести эти массивы в матричном и табличном виде, получить их таблицы вывода.
5 Исследовать следующие свойства матриц на примере преобразования заданных массивов:
5.1 Транспонированная матрица суммы двух матриц равна сумме транспонированных матриц  .
.
5.2 Транспонированная матрица произведения двух матриц равна произведению транспонированных матриц, взятых в обратном порядке: 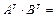
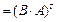 .
.
5.3 При умножении матрицы размером m × n на вектор последний должен являться столбцом из n элементов.
5.4 При умножении вектора на матрицу размером m × n первый должен являться строкой из m элементов.
5.5 При транспонировании квадратной матрицы определитель не меняется: 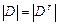 .
.
5.6 Произведение квадратной матрицы на соответствующую ей обратную дает единичную матрицу (элементы главной диагонали единичной матрицы равны 1, а все остальные – 0): 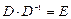 .
.
6 Создать способом ввода отдельных элементов вектор g и матрицу H размером 5×1 и 5×5 соответственно.
7 Создать с помощью ранжированной переменной вектор k и матрицу L размером 5×1 и 5×5 соответственно путем непосредственного ввода значений (пример 3.1).
8 Создать с помощью ранжированной переменной (пример 3.2) вектор x и матрицу Y размером 5×1 и 5×5 соответственно. Формулы для вычисления значений элементов см. в таблице 3.3, где i, j – ранжированные переменные. Вывести эти массивы.
9 Создать матрицу Y1 размером 5×5, состоящую из случайных чисел, равномерно распределенных на интервале от минус 2 до 2 (пример 3.3).
10 Создать матрицу Y2 размером 5×5 с помощью функции matrix (пример 3.4). Формулу  для вычисления значений элементов см. в таблице 3.3.
для вычисления значений элементов см. в таблице 3.3.
Формулы для создания массивов с помощью
ранжированной переменной и функции matrix Таблица 3
| Вариант
| Вектор x
| Матрица Y
| f (i, j)
|
|
| 
| 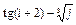
| 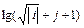
|
|
| 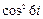
| 
| 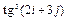
|
|
| 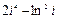
| 
| 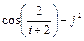
|
|
| 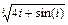
| 
| 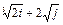
|
|
| 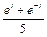
| 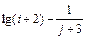
| 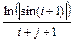
|
|
| 
| 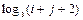
| 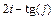
|
|
| 
| 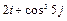
| 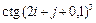
|
|
| 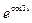
| 
| 
|
|
| 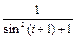
| 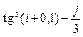
| 
|
|
| 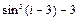
| 
| 
|
|
| 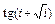
| 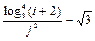
| 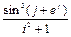
|
|
| 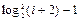
| 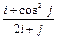
| 
|
|
| 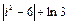
| 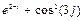
| 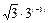
|
|
| 
| 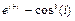
| 
|
|
| 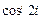
| 
| 
|
|
| 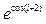
| 
| 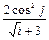
|
11 Записать в файл task1.prn вектор. Записать в файл task2.prn матрицу. Просмотреть полученные файлы в Блокноте.
12 Дописать в файл task2.prn произвольную матрицу. Просмотреть полученный файл в Блокноте.
13 Ввести значения в матрицу (имя произвольное) из структурированного файла данных task2.prn, используя функцию чтения данных.
14 Создать в Блокноте файл данных с именем task3.prn, размещенных структурировано в виде таблицы. Элементы можно отделять с помощью клавиши Tab. Ввести значения в матрицу (имя произвольное) из структурированного файла данных task3.prn, используя функцию чтения данных.
15 Получить матрицу M по формуле  .
.
16 Подсчитать минимальный, максимальный элемент, сумму и произведение элементов матрицы M.
17 Получить вектор-столбец v 1 по значениям (mod (n, 5)+1)-го столбца и вектор-столбец v 2 по значениям (5 − mod (n, 5))-й строки матрицы M, где n − номер варианта. Подсчитать минимальный, максимальный элемент, сумму, длину, скалярное и векторное произведения элементов векторов v 1 и v 2.
18 Получить массив из элементов матрицы M, стоящих на пересечениях 2-й, 3-й строк и 3-го, 4-го столбцов. Получить массив, объединив матрицы A, B, M по строкам. Получить массив, объединив матрицы A, M по столбцам.
19 Далее продолжать работу по вариантам (таблица 3.4), используя функцию if, известные векторные и матричные операции и функции.
Применение векторных и матричных операций и функций Таблица 4
| Вариант
| Задача
|
|
| Элементы матрицы M, которые больше числа 5, заменить числом 5. Подсчитать сумму элементов M, сумма индексов которых − четная. Вывести второй столбец матрицы M. Отсортировать его по убыванию. По созданному вектору получить матрицу M 1 с элементами этого вектора на главной диагонали. Заменить элементы первого столбца матрицы M 1средним арифметическим элементов матрицы. Создать подматрицу M 2 из нечетных строк матрицы M 1, каждый элемент M 2 уменьшить на единицу
|
|
| Создать вектор d из элементов главной диагонали матрицы M и отсортировать его по возрастанию. Подсчитать минимальный элемент во второй строке матрицы M. Найти синус каждого элемента матрицы M, результат сохранить в матрице M 1. Подсчитать сумму отрицательных элементов матрицы M1. Заменить отрицательные и нулевые элементы матрицы M 1 на 1. Найти среднее геометрическое M 1. Создать подматрицу M 2 из нечетных столбцов матрицы M 1
|
|
| Преобразовать матрицу M таким образом, чтобы отсортированным оказался третий столбец. Подсчитать сумму элементов матрицы M, стоящих выше главной диагонали. Определить максимальные элементы в нечетных столбцах матрицы M и их среднее арифметическое. Получить матрицу M 1, на главной диагонали которой − третья строка матрицы M. Найти косинус каждого элемента M. Создать подматрицу M 2 из нечетных строк и столбцов матрицы M 1
|
|
| Элементы матрицы M, которые по модулю больше 10, заменить числом 10. Подсчитать произведение диагональных элементов матрицы M. Определить максимальные элементы в четных столбцах матрицы M и во второй строке. Отсортировать вторую строку M по убыванию. Подсчитать тангенс каждого элемента матрицы M. Получить матрицу M1 из первого и третьего столбцов матрицы M
|
|
| Подсчитать среднее геометрическое положительных элементов матрицы M. Определить максимальные элементы в нечетных строках матрицы M. Третий столбец матрицы M отсортировать по возрастанию и создать на его основе диагональную матрицу M1. Нулевые элементы M1 заменить значением определителя M1. Найти синус каждого элемента полученного массива. Заменить положительные элементы второго столбца полученного массива его определителем
|
|
| Подсчитать сумму элементов матрицы M, стоящих ниже главной диагонали. Создать из элементов главной диагонали матрицы M вектор z и отсортировать его по убыванию. Элементы третьего и четвертого столбцов матрицы M заменить модулем вектора z. Получить матрицу M1, объединив матрицу M и вектор, составленный из косинусов элементов вектора z
|
|
| Заменить элементы второго столбца матрицы M их модулями. Удвоить матрицу M, добавив к ней справа такую же матрицу. Создать матрицу M1 размерностью 5×5 из элементов удвоенной матрицы M, стоящих в строках с 1-й по 5-ю и в столбцах с 3-го по 7-й. Вычислить среднее арифметическое элементов матрицы M1. Подсчитать максимальный элемент главной диагонали матрицы M1
|
|
| Округлить дробные элементы матрицы M. Подсчитать максимальные элементы в каждом нечетном столбце матрицы M. Четвертую строку матрицы M отсортировать по возрастанию. Создать подматрицу M1 матрицы M, состоящую из ее нечетных столбцов. Получить матрицу извлечением кубического корня из элементов матрицы M1. Найти ранг матрицы M1 и заменить полученным значением элементы главной диагонали
|
|
| Создать подматрицу M1 матрицы M, состоящую из элементов, стоящих в нечетных строках и столбцах M. Подсчитать сумму элементов полученного массива M1. Инвертировать его. Найти минимальный элемент полученной обратной матрицы и заменить им элементы главной диагонали матрицы M. Подсчитать котангенс каждого элемента матрицы M. Заменить отрицательные элементы второй строки M единицей
|
|
| Элементы матрицы M, которые по модулю меньше 3, заменить числом 3. Транспонировать полученный массив, в котором определить минимальный элемент в четвертой строке. Определить среднее геометрическое элементов полученного массива. Подсчитать косинус каждого элемента массива M и поместить в матрицу M1. Найти произведение элементов M1, стоящих ниже главной диагонали
|
|
| Подсчитать сумму элементов матрицы M, стоящих не ниже главной диагонали. Первую строку матрицы M заменить элементами главной диагонали. Подсчитать максимальные элементы в каждом четном столбце. Создать подматрицу M1 матрицы M, размерностью 3×3, состоящую из элементов, стоящих в первых трех строках и столбцах M. Элементы главной диагонали новой матрицы увеличить на единицу
|
|
| Отрицательные элементы матрицы M заменить их модулями. Найти ранг и сумму диагональных элементов полученной матрицы. Подсчитать сумму элементов матрицы M, стоящих выше главной диагонали. Найти минимальный элемент в третьей строке M. На основе первой строки матрицы M создать диагональную матрицу M1 и умножить ее на исходную матрицу поэлементно
|
|
| Преобразовать матрицу M так, чтобы отсортированной оказалась вторая строка. Элементы главной диагонали матрицы M заменить единицей и инвертировать полученную матрицу. Подсчитать минимальные элементы в четных строках полученной матрицы M -1. Подсчитать сумму элементов 1-го столбца матрицы M. Элементы M, сумма индексов которых равна 3, заменить определителем M
|
|
| Получить матрицу M1, каждый элемент которой – квадратный корень из элементов матрицы M. Комплексные элементы полученной матрицы заменить их мнимыми частями, действительные элементы не изменять. Из каждого элемента матрицы M вычесть 10. В полученной матрице определить минимальный элемент во второй строке и сумму элементов, у которых хотя бы один из индексов четный
|
|
| Подсчитать произведение дробных частей элементов матрицы M. Создать вектор d из элементов главной диагонали, отсортировать его по убыванию. Заменить вектором d последний столбец матрицы M. Вычислить косинус каждого элемента матрицы M. Определить сумму элементов второй строки матрицы M и заменить этой суммой элементы, у которых один из индексов нечетный
|
|
| Подсчитать произведение элементов матрицы M, сумма индексов которых – четная. Определить среднее арифметическое в каждом столбце матрицы M, данные представить в виде вектора. Вектор отсортировать по убыванию. На основе полученного вектора создать диагональную матрицу M1 и определить ее минимальный элемент. Подсчитать котангенс каждого элемента полученной матрицы
|
| | | |
20 Подготовить документ для печати и распечатать. Завершить работу.
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ
По формуле 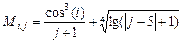 задать матрицу M размерностью 7×7. Получить подматрицу M1 размерностью 5×5 из элементов M, стоящих на пересечении последних пяти строк и столбцов. Подсчитать произведение элементов матрицы M1 с нечетной суммой индексов. Создать матрицу M2, каждый элемент которой – натуральный логарифм матрицы M1. Комплексные элементы матрицы M2 заменить их действительной частью. Найти максимальные элементы в нечетных столбцах M2. Сформировать вектор z из диагональных элементов матрицы M2 и найти его модуль. Создать матрицу M3 из нечетных строк матрицы M2 и вектора z.
задать матрицу M размерностью 7×7. Получить подматрицу M1 размерностью 5×5 из элементов M, стоящих на пересечении последних пяти строк и столбцов. Подсчитать произведение элементов матрицы M1 с нечетной суммой индексов. Создать матрицу M2, каждый элемент которой – натуральный логарифм матрицы M1. Комплексные элементы матрицы M2 заменить их действительной частью. Найти максимальные элементы в нечетных столбцах M2. Сформировать вектор z из диагональных элементов матрицы M2 и найти его модуль. Создать матрицу M3 из нечетных строк матрицы M2 и вектора z.
Определяем переменную ORIGIN и ранжированные переменные для нумерации элементов массивов:
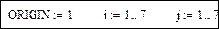
Задаем матрицу M и ее подматрицу M1:
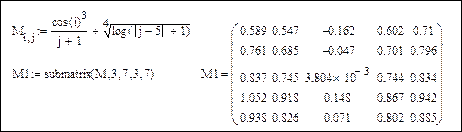
Для подсчета произведения элементов матрицы M1 с нечетной суммой индексов создаем с помощью оператора if вспомогательную матрицу, в которой на указанных местах стоят элементы M1, а на местах с четной суммой индексов – единицы. Произведение элементов такой вспомогательной матрицы будет искомым:
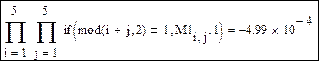
Для создания матрицы M2 достаточно использовать «векторизацию»:
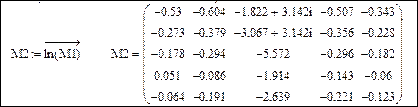
Заменим комплексные элементы матрицы M2 их действительной частью, используя функцию Re(z), возвращающую действительную часть числа z:
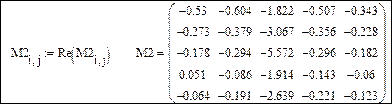
Максимальные элементы в нечетных столбцах представим в виде ранжированной переменной:

Создадим вектор z из элементов матрицы M2 и найдем его модуль:

Для создания матрицы M3 можно, например, использовать функцию объединения массивов с одинаковым количеством строк:
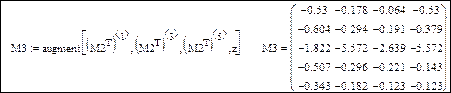
КОНТРОЛЬНОЕ ЗАДАНИЕ
1 Задать произвольную матрицу M размером 5×4 и вектор v размером 5×1, элементы которого определяются по формуле  , где x – произвольное число.
, где x – произвольное число.
2 Объединить массивы M и v в матрицу A размерностью 5×5. Вывести M в виде таблицы, A – в матричном виде, v отсортировать по убыванию и вывести в виде таблицы вывода ранжированной переменной.
3 Найти максимальный элемент матрицы A, сумму диагональных элементов, определитель матрицы A.
4 Подсчитать сумму элементов матрицы А.
5 Инвертировать матрицу A. В полученном массиве определить максимальные элементы в четных столбцах.
6 В матрице A -1 определить произведение положительных элементов.
7 Записать матрицу А в файл данных и просмотреть его в Блокноте.
Приблизительная оценка выполнения контрольного задания (время выполнения 20 минут):
| Номера заданий
| Оценка
|
| 1−7
| 9-10
|
| 1−5, 7
|
|
| 1−4, 7
| 6-7
|
| 1, 2, 4, 5
|
|
| 1, 2, 4
|
|
КОНТРОЛЬНЫЕ ВОПРОСЫ
1 Что такое массив?
2 Что такое матрица? Что такое вектор в Mathcad? Какие бывают векторы в Mathcad?
3 Что такое ORIGIN и как она задается?
4 Перечислить способы создания массивов.
5 Как добавить строку или столбец в уже существующий массив?
6 Указать способы вывода и отображения массивов.
7 Перечислить операции для работы с массивами.
8 Перечислить и определить векторные функции.
9 Перечислить и определить функции для создания массивов.
10 Перечислить и определить функции, возвращающие специальные характеристики массивов.
11 Перечислить и определить функции сортировки массивов.
Перечислить функции для работы с файлами данных
СПИСОК ЛИТЕРАТУРЫ
1. Голдобина, Т. А. MathCad для экономистов / Учеб.-метод. пособие по дисциплине "Компьютерные информационные технологии". – Гомель: БелГУТ, 2007. – 107 с.
2. Дьяконов И.И. Использование системы MathCad.– Киев: Диалектика, 1999.– 386 с.
3. Кирьянов Д.А. Самоучитель MathCad 11.– Санкт-Петербург: БВХ- Петербург, 2003.– 540 с.
4. Симанович С.В. Информатика. Базовый курс. – Санкт-Петербург: Питер, 2004.– 640с.
5. Гурский Д.А., Турбина Е.А. MathCad для студентов и школьников. Популярный самоучитель.– Санкт-Петербург: БВХ- Петербург, 2005.– 40 с.
6. Гурский Д.А., Турбина Е.А. Вычисления MathCad 12 – Санкт-Петербург: Питер, 2006.– 546с.
Учебное издание
ЧИСЛЕННЫЕ МЕТОДЫ
Методические указания к выполнению лабораторной работы
№3-4 по курсу «Численные методы» для студентов, обучающихся
по направлению 230700 «Прикладная информатика»,
всех форм обучения
Составитель:
СОКОЛОВА Светлана Васильевна
Печатается в редакции составителя



 .
.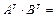
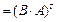 .
.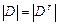 .
.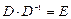 .
. для вычисления значений элементов см. в таблице 3.3.
для вычисления значений элементов см. в таблице 3.3.
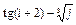
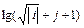


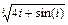

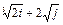
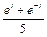
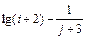
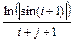

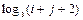
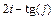

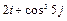
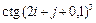
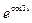


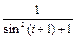
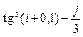

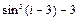


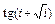
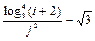
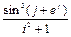
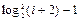
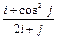

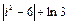
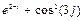





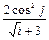
 .
.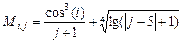 задать матрицу M размерностью 7×7. Получить подматрицу M1 размерностью 5×5 из элементов M, стоящих на пересечении последних пяти строк и столбцов. Подсчитать произведение элементов матрицы M1 с нечетной суммой индексов. Создать матрицу M2, каждый элемент которой – натуральный логарифм матрицы M1. Комплексные элементы матрицы M2 заменить их действительной частью. Найти максимальные элементы в нечетных столбцах M2. Сформировать вектор z из диагональных элементов матрицы M2 и найти его модуль. Создать матрицу M3 из нечетных строк матрицы M2 и вектора z.
задать матрицу M размерностью 7×7. Получить подматрицу M1 размерностью 5×5 из элементов M, стоящих на пересечении последних пяти строк и столбцов. Подсчитать произведение элементов матрицы M1 с нечетной суммой индексов. Создать матрицу M2, каждый элемент которой – натуральный логарифм матрицы M1. Комплексные элементы матрицы M2 заменить их действительной частью. Найти максимальные элементы в нечетных столбцах M2. Сформировать вектор z из диагональных элементов матрицы M2 и найти его модуль. Создать матрицу M3 из нечетных строк матрицы M2 и вектора z.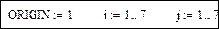
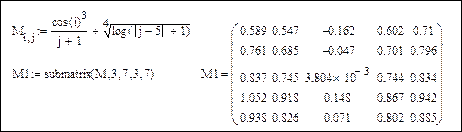
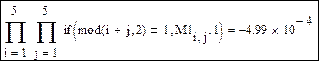
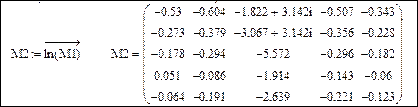
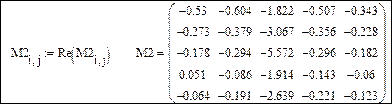


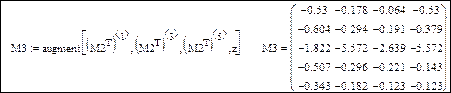
 , где x – произвольное число.
, где x – произвольное число.


