Для модели идеального смешения принимается ряд допущений.
1) Допускается, что в результате интенсивного перемешивания устанавливаются абсолютно одинаковые условия в любой точке реактора: концентрации реагентов и продуктов, степени превращения реагентов, температура, скорость химической реакции и т. д. Например, в некоторый момент времени  - во всех точках реактора (рис. 2) выполняются следующие условия:
- во всех точках реактора (рис. 2) выполняются следующие условия:
 ; (7)
; (7)
 ;
;  ;
;  ; (8)
; (8)
где х, y, z —пространственные координаты.
2) В проточном реакторе идеального смешения концентрации участников реакции в выходном потоке в рассматриваемый момент времени  строго равны концентрациям тех же веществ в реакторе.
строго равны концентрациям тех же веществ в реакторе.

| Рис2 Схематическое изображение реакторов идеального смешения:
а-с механическим перемешивающим устройством; б - с циркуляционным контуром
|
3) Чтобы перечисленные допущения могли быть выполнены, необходимо принять еще одно допущение: переход от одной концентрации к другой в реакторе идеального смешения не должен иметь протяженности во времени. Изменение концентрации исходного реагента от начальной 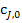 во входном потоке в данный момент времени
во входном потоке в данный момент времени  до концентрации в реакторе
до концентрации в реакторе  в этот же момент времени должно происходить мгновенно (скачкообразно).
в этот же момент времени должно происходить мгновенно (скачкообразно).
Приблизиться к режиму идеального смешения можно, обеспечив интенсивное перемешивание реакционной смеси с помощью механических мешалок разного типа или циркуляционных насосов, создающих высокую кратность циркуляции. Смешение, близкое к идеальному, легче осуществить в емкостных аппаратах с приблизительно равными диаметром и высотой.
Так как в реакторе идеального смешения концентрации участников реакции равномерно распределены по объему, то уравнение материального баланса (6), выведенное для элементарного объема, можно распространить на полный объем реактора.
Периодический РИС. В периодический реактор все реагенты вводят до начала реакции, а все продукты выводят из него только после окончания процесса; в ходе реакционного цикла никаких веществ в реактор не вводят и из него не выводят, так что общая масса реакционной смеси в реакторе остается постоянной, а изменяется лишь ее состав.
Из общего уравнения материального баланса (6) в случае периодического реактора идеального смешения можно исключить два первых оператора, описывающих явления конвективного и диффузионного переноса вещества в аппарате. При отсутствии перемещения потока через реактор в произвольный момент времени между началом и окончанием процесса средняя линейная скорость элемента потока равна нулю, следовательно, и конвективный перенос в непроточном реакторе отсутствует. Заключение об отсутствии диффузионного переноса вытекает из допущений модели идеального смешения, так как диффузия возможна лишь при наличии градиента концентраций, а при равномерном распределении концентраций по объему он равен нулю.
Следовательно, уравнение материального баланса для периодического реактора идеального смешения примет вид
 ; (9)
; (9)
(В уравнении (9) частная производная заменена на полную, так как в соответствии с допущениями идеального смешения концентрация 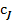 внутри реактора является функцией только одной переменной — времени.)
внутри реактора является функцией только одной переменной — времени.)
Для проведения расчетов по уравнению (9) в его левую часть вместо 𝜔rJ надо подставить соответствующее кинетическое уравнение 𝜔rJ ( 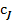 ) итогда можно рассчитать, например, время реакционного цикла, необходимое для достижения заданной глубины превращения (заданной конечной концентрации
) итогда можно рассчитать, например, время реакционного цикла, необходимое для достижения заданной глубины превращения (заданной конечной концентрации  ):
):
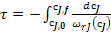 . (10)
. (10)
Если вещество J — исходный реагент, то концентрацию 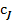 можно выразить через его степень превращения:
можно выразить через его степень превращения:
 , (11)
, (11)
Тогда  (12)
(12)
и уравнение (10) примет вид
 . (13)
. (13)
Периодические реакторы с интенсивным перемешиванием, приближающимся к идеальному смешению, применяют в производствах реактивов, органических красителей, лекарственных препаратов. — там, где для достижения достаточной глубины превращения требуется сравнительно длительное время, а объемы производства невелики. Периодические реакторы смешения часто применяют в микробиологической промышленности для культивирования аэробных микроорганизмов. Как правило, периодические процессы выгодны при относительно невысокой производственной мощности в тех случаях, когда получают дорогостоящие продукты.
Проточный РИС. Если необходимо обеспечить получение большого количества продукта одинакового качества, химический процесс предпочитают проводить в непрерывнодействующих реакторах с установившимся режимом. Рассмотрим уравнение материального баланса для стационарного проточного реактора идеального смешения без циркуляции. Получим его, опять упрощая общее уравнение материального баланса (6). Для любого реактора идеального смешения и, в частности для проточного, из уравнения можно исключить оператор, описывающий диффузионный перенос. При стационарном режиме работы реактора из уравнения исключается производная  /
/  , не равная нулю только при наличии накопления вещества в реакторе.
, не равная нулю только при наличии накопления вещества в реакторе.
Таким образом, в уравнении остаются только два члена, описывающие конвективный перенос вещества J и расход или образование этого веществам в ходе химической реакции.
Оператор конвективного переноса (переноса импульса), записанный в уравнении (6) в дифференциальной форме, можно представить для протонного реактора идеального смешения в конечно-разностной форме. В соответствии с допущениями модели идеального смешения в проточном реакторе происходит дискретное конечное (а не бесконечно малое) изменение концентрации  сразу же на входе в реактор. Заменим поэтому градиент концентрации на отношение конечного изменения концентрации
сразу же на входе в реактор. Заменим поэтому градиент концентрации на отношение конечного изменения концентрации  к изменению координаты ∆z при прохождении реакционного потока через реактор со средней линейной скоростью
к изменению координаты ∆z при прохождении реакционного потока через реактор со средней линейной скоростью  . Среднюю линейную скорость потока можно заменить через отношение объемного расхода v через реактор к площади поперечного сечения F. Тогда, с учетом того, что произведение F∆z равно объему реактора V, член уравнения описывающий конвективный перенос, примет вид
. Среднюю линейную скорость потока можно заменить через отношение объемного расхода v через реактор к площади поперечного сечения F. Тогда, с учетом того, что произведение F∆z равно объему реактора V, член уравнения описывающий конвективный перенос, примет вид
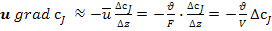 . (14)
. (14)
В выражении (14)  равно разности концентраций на выходе из реактора
равно разности концентраций на выходе из реактора  , и на входе в реактор
, и на входе в реактор  . Окончательно уравнение материального баланса проточного стационарного реактора идеального смешения можно представить так:
. Окончательно уравнение материального баланса проточного стационарного реактора идеального смешения можно представить так:
 (15)
(15)
или
 . (16)
. (16)
Величина  в уравнении (16) измеряется в единицах времени и характеризует среднее время, в течение которого обновляется содержание проточного реактора.
в уравнении (16) измеряется в единицах времени и характеризует среднее время, в течение которого обновляется содержание проточного реактора.
Для решения практических задач удобно концентрацию реагента  выразить через его степень превращения
выразить через его степень превращения 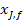
 . (17)
. (17)
Пример 1. Рассчитать среднее время пребывания реагентов в проточном реакторе идеального смешения, необходимое для достижения степени превращения исходного реагентаr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  .
.
В реакторе протекает реакция второго порядка  , скорость которой описывается при постоянной температуре кинетическим уравнением
, скорость которой описывается при постоянной температуре кинетическим уравнением  . Начальная концентрация реагента А на входе в реактор
. Начальная концентрация реагента А на входе в реактор  .
.
Решение. Для определения т можно использовать уравнение (17); концентрацию реагента в реакторе, необходимую для расчета скорости протекающей в нем реакции, выразим через степень превращения

Таким образом, для достижения степени превращения хА = 0,8 необходимо, чтобы соотношение между объемом реактора и объемным расходом через нега составляло  .
.
Реактор идеального вытеснения (РИВ)
Реактор идеального вытеснения представляет собой длинный канал, через который реакционная смесь движется в поршневом режиме (рис. 3). Каждый элемент потока, условно выделенный двумя плоскостями, перпендикулярными оси канала, движется через него как твердый поршень, вытесняя предыдущие элементы потока и не перемешиваясь ни с предыдущими, ни со следующими за ним элементами.
 Идеальное вытеснение возможно при выполнении следующих допущений: 1) движущийся поток имеет плоский профиль линейных скоростей; 2)отсутствует обусловленное любыми причинами перемешивание в направлении оси потока; 3) в каждом отдельно взятом сечении, перпендикулярном оси потока, параметры процесса (концентрации, температуры и т.д.) полностью выровнены
Идеальное вытеснение возможно при выполнении следующих допущений: 1) движущийся поток имеет плоский профиль линейных скоростей; 2)отсутствует обусловленное любыми причинами перемешивание в направлении оси потока; 3) в каждом отдельно взятом сечении, перпендикулярном оси потока, параметры процесса (концентрации, температуры и т.д.) полностью выровнены
| Рис. 3. Схематическое изображение реактора идеального вытеснения
|
В реальном реакторе можно приблизиться к режиму идеального вытеснения, если реакционный поток — турбулентный и при этом длина канала существенно превышает его поперечный размер (например, для цилиндрических труб L/D > 20).
В соответствии с принятыми допущениями общее уравнение материального баланса (6) для элементарного объема проточного реактора можно упростить. Прежде всего в качестве элементарного объема в этом случае можно рассматривать объем, вырезанный двумя параллельными плоскостями, находящимися друг от друга на бесконечно малом расстоянии dz и перпендикулярными оси канала z (см. рис. 3). В этом элементарном объеме в соответствии с третьим допущением dcj/dx = 0 и dcj/dy = 0. Следовательно, конвективный перенос происходит только в направлении оси z. В соответствии со вторым и третьим допущениями диффузионный перенос в реакторе идеального вытеснения отсутствует (как и в реакторе смешения). Следовательно, уравнение (6) для реактора идеального вытеснения в нестационарном режиме работы примет вид
 . (18)
. (18)
При стационарном режиме:
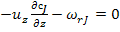 . (19)
. (19)
В реакторе с постоянной площадью поперечного сечения канала линейная скорость потока uz будет величиной постоянной, равной отношению объемного расхода v к площади сечения  Тогда, с учетом того, что
Тогда, с учетом того, что  , уравнение (19) можно записать в таком виде:
, уравнение (19) можно записать в таком виде:
 . (20)
. (20)
Уравнение (20) для стационарного режима реактора идеального вытеснения можно проинтегрировать относительно  ;
;
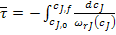 (21)
(21)
или, если J — исходный реагент,
 . (22)
. (22)
Уравнения (22), (21) по виду напоминают уравнения (10), (13) для периодического реактора идеального смешения. Если считать, что элементарный объем dV, для которого составлялся материальный баланс, может двигаться месте с потоком, то в поршневом режиме он может рассматриваться как своеобразный периодический микрореактор идеального смешения, время проведения реакции в котором равно среднему времени пребывания реагентов в реакторе идеального вытеснения.
Пример 2. Определить среднее время пребывания реагентов в проточном реакторе идеального вытеснения для условий примера 5. 1(реакция второго порядка 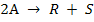 , кинетическое уравнение
, кинетическое уравнение  = 2,5
= 2,5 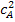 ,
,  = 4 кмоль/
= 4 кмоль/  ,
,  = 0,8).
= 0,8).
Решение. Используем для расчета уравнение (23):
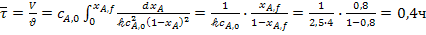 .
.
Таким образом, для достижения аналогичных результатов значение  для реактора идеального вытеснения (0,4 ч) существенно меньше, чем значение
для реактора идеального вытеснения (0,4 ч) существенно меньше, чем значение  для проточного реактора идеального смешения.
для проточного реактора идеального смешения.



 - во всех точках реактора (рис. 2) выполняются следующие условия:
- во всех точках реактора (рис. 2) выполняются следующие условия: ; (7)
; (7) ;
;  ;
;  ; (8)
; (8)
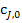 во входном потоке в данный момент времени
во входном потоке в данный момент времени  в этот же момент времени должно происходить мгновенно (скачкообразно).
в этот же момент времени должно происходить мгновенно (скачкообразно). ; (9)
; (9)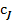 внутри реактора является функцией только одной переменной — времени.)
внутри реактора является функцией только одной переменной — времени.) ):
):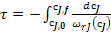 . (10)
. (10) , (11)
, (11) (12)
(12) . (13)
. (13) /
/  , не равная нулю только при наличии накопления вещества в реакторе.
, не равная нулю только при наличии накопления вещества в реакторе. сразу же на входе в реактор. Заменим поэтому градиент концентрации на отношение конечного изменения концентрации
сразу же на входе в реактор. Заменим поэтому градиент концентрации на отношение конечного изменения концентрации  . Среднюю линейную скорость потока можно заменить через отношение объемного расхода v через реактор к площади поперечного сечения F. Тогда, с учетом того, что произведение F∆z равно объему реактора V, член уравнения описывающий конвективный перенос, примет вид
. Среднюю линейную скорость потока можно заменить через отношение объемного расхода v через реактор к площади поперечного сечения F. Тогда, с учетом того, что произведение F∆z равно объему реактора V, член уравнения описывающий конвективный перенос, примет вид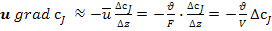 . (14)
. (14) . Окончательно уравнение материального баланса проточного стационарного реактора идеального смешения можно представить так:
. Окончательно уравнение материального баланса проточного стационарного реактора идеального смешения можно представить так: (15)
(15) . (16)
. (16) в уравнении (16) измеряется в единицах времени и характеризует среднее время, в течение которого обновляется содержание проточного реактора.
в уравнении (16) измеряется в единицах времени и характеризует среднее время, в течение которого обновляется содержание проточного реактора. выразить через его степень превращения
выразить через его степень превращения 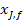
 . (17)
. (17) .
. , скорость которой описывается при постоянной температуре кинетическим уравнением
, скорость которой описывается при постоянной температуре кинетическим уравнением  . Начальная концентрация реагента А на входе в реактор
. Начальная концентрация реагента А на входе в реактор  .
.
 .
. Идеальное вытеснение возможно при выполнении следующих допущений: 1) движущийся поток имеет плоский профиль линейных скоростей; 2)отсутствует обусловленное любыми причинами перемешивание в направлении оси потока; 3) в каждом отдельно взятом сечении, перпендикулярном оси потока, параметры процесса (концентрации, температуры и т.д.) полностью выровнены
Идеальное вытеснение возможно при выполнении следующих допущений: 1) движущийся поток имеет плоский профиль линейных скоростей; 2)отсутствует обусловленное любыми причинами перемешивание в направлении оси потока; 3) в каждом отдельно взятом сечении, перпендикулярном оси потока, параметры процесса (концентрации, температуры и т.д.) полностью выровнены . (18)
. (18)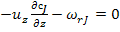 . (19)
. (19) Тогда, с учетом того, что
Тогда, с учетом того, что  , уравнение (19) можно записать в таком виде:
, уравнение (19) можно записать в таком виде: . (20)
. (20) ;
;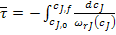 (21)
(21) . (22)
. (22) , кинетическое уравнение
, кинетическое уравнение  = 2,5
= 2,5 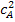 ,
,  = 4 кмоль/
= 4 кмоль/  ,
,  = 0,8).
= 0,8).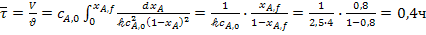 .
. для реактора идеального вытеснения (0,4 ч) существенно меньше, чем значение
для реактора идеального вытеснения (0,4 ч) существенно меньше, чем значение 


