Моделирование, общие понятия
Задача моделирования – исследование сложных объектов или процессов на их физических или математических моделях. Цель моделирования – найти оптимальное (наилучшее по каким-либо критериям) техническое решение. Виды моделирования:
Ø физическое;
Ø математическое;
Ø графическое (геометрическое).
При моделировании происходит замена наиболее важных свойств изучаемой системы строгими, но упрощенными по отношению к исходному природному явлению научными формулировками – моделями. Модель обеспечивает возможность точного описания и предсказания поведения системы, но только в строго ограниченной области применения — пока справедливы те исходные упрощения, на основе которых модель и строилась.
Например, при моделировании полета спутника вокруг Земли его стенки можно считать абсолютно твердым, а при моделировании столкновения того же спутника с микрометеоритом даже сверхтвердое железо можно с очень большой точностью описывать как идеальную несжимаемую жидкость. В этом парадоксальная особенность моделирования – его точность, вызванная к жизни принципиально неточными, по самой своей сущности приближенными, годными только в определенной области явлений, моделями реальной системы.
Процессы функционирования и структуру системы можно описать посредством математического моделирования. Математическое моделирование – процесс создания математической модели и действий с ней с целью получения сведений о реальной системе. Математическая модель – совокупность математических объектов и связей между ними, которая адекватно отражает важнейшие свойства системы. Математические объекты – числа, переменные, матрицы и т.п. Связи между математическими объектами – уравнения, неравенства и т.п. Любые научно-технические расчеты являются специализированными видами математического моделирования.
Система – множество закономерно связанных друг с другом элементов, образующих единую целостность, с указанием связей между ними и цели функционирования. Свойства системы отличаются от суммы свойств ее элементов. Примеры: Станок ¹ å(детали + узлы); Человек ¹ å(мозг + печень + позвоночник).
Методика получения математической модели
При построении математической модели выделяют следующие типовые шаги:
1) Выбор свойств системы, которые должны получить отражение в модели. Например, для модели обрабатываемости резанием учитывают твердость материала, но во многих случаях пренебрегают теплоемкостью.
2) Сбор исходной информации о выбранных свойствах системы. Например, в зависимости от скорости резания меняются условия работы режущего клина (образование нароста, высокоскоростное фрезерование). Поэтому ММ для расчета силы резания при протягивании и высокоскоростном фрезеровании могут отличаться.
3) Синтез структуры модели. Имеется в виду создание математических соотношений общего вида, без конкретных числовых значений параметров. Наиболее часто определяется либо из физических принципов функционирования системы, либо из вида эмпирических зависимостей. Например, вид зависимости силы резания от S, t, v.
4) Расчет числовых значений параметров. Например, из результатов эксперимента, обработанных по методу наименьших квадратов.
5) Оценка точности и адекватности математической модели, определение области применимости. Заключается, например, в сравнение предсказанных моделью и фактически наблюдаемых результатах.
Требования к математической модели
Основные требования к математическим моделям:
1. Универсальность – применимость ММ к анализу группы однотипных систем.
2. Точность – оценивается степенью совпадения параметров реального объекта и значений тех же параметров, рассчитанных с помощью математической модели. Относительная погрешность e расчета выходного параметра yравна:
e = (y факт – y мод)/y факт.
3. Адекватность – способность отражать заданные свойства системы с погрешностью не выше заданной. Адекватность ММ имеет место только в ограниченной области изменения внешних параметров, которая называется областью адекватности математической модели.
4. Важной характеристикой ММ является устойчивость решения. Например, система уравнений
25×X – 36×Y = 1
16×X – 23×Y = –1
имеет решение – X=–59, Y=–41, но изменение значения коэффициентов всего на 0.01 меняет решение качественно:
| 25.01×X – 36×Y = 1
15.99×X – 23.01×Y = –1
| 25.01×X – 35.99×Y = 1
15.99×X – 23.01×Y = –1
|
| НАЙТИ РЕШЕНИЯ САМОСТОЯТЕЛЬНО
|
| X=????.??, Y=????.??
| X=????.??, Y=????.??
|
5. Экономичность – характеризуется затратами ресурсов ЭВМ (времени счета, необходимым требованиям к памяти и т.д.) на реализацию ММ.
Метод конечных разностей
Метод конечных разностей – самый старый метод решения краевых задач. Производная функции заменяется отношением разности ее значений при малом изменении аргумента к изменению аргумента. Например, для функции y(x) на отрезке (одномерная задача), пользуясь разложением по формуле Тейлора, можно записать:

 ,
,
где h – малое изменение аргумента, в данном случае x. Проще всего понять суть метода на примере. Пусть требуется найти решение уравнения (значение функции j при заданном X):
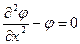 ,
,
удовлетворяющего следующим граничным условиям (ГУ) или значениям на границах исследуемой области (0 £ X £ 1):
j (х=0) = 0;
j (x=1) = 1.
Разбиваем область определения от 0 до 1 на 3 элемента. Иными словами, шаг сетки h равен h=1/3.

Заменяя вторую производную в дифференциальном уравнении ее аппроксимацией по формуле Тейлора, для i-го узла получаем:
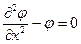
|
| ¯
|

|
или, после приведения подобных
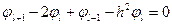 .
.
Используя это уравнение, для узлов i=1 и i=2 можно записать систему линейных алгебраических уравнений:

 (i=1)
(i=1)
 (i=2)
(i=2)
Подставляя значения граничных условий: j 0 =0 и j 3 =1, получаем итоговую систему алгебраических уравнений:
Ее решение: j 1 =0.2893 и j 2 =0.6107. Точное решение: j 1 =0.2889 и j 2 =0.6102.
Аналогичным образом можно решать задачи и в 2-, 3-мерных областях. Например, для двухмерной задачи отдельно аппроксимируются производные по X и Y. Для этого используются следующие «шаблоны»:

К преимуществам метода конечных разностей можно отнести возможность относительно просто (для профессионала) решать сколь угодно сложные задачи. К недостаткам – сложность задания неравномерной сетки в исследуемой области и проблемы задания ГУ на границах, непараллельных осям координат.
Метод граничных элементов
Основан на замене исходного дифференциального уравнения системой интегральных уравнений. Искомое решение ищется как сумма решений задачи для множества фиктивных источников, мощность которых подобрана так, что их суммарное воздействие обеспечивает заданные граничные условия. В простейшем случае границу объекта заменяют многоугольником, на каждой стороне которого действует фиктивный источник неизвестной мощности.
Например, для 4-угольника граничные условия – температура на гранях. Подбираются фиктивные источники тепла, которые в сумме обеспечивают заданную температуру на каждой грани. Зная мощность источников, легко рассчитать температуру в любой точке внутри 4-угольника.

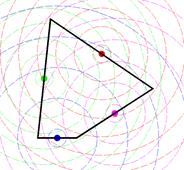
(+) Часто обеспечивает большую точность и резко уменьшает объем исходных данных, необходимых для решения. (–) МГЭ используется только для линейных задач. Он сложнее в реализации чем, например, метод конечных элементов.
Метод конечных элементов
Рассмотрим использование метода конечных элементов на примере прочностного расчета пластины (рисунок 1, а). Пластина (показана тонкими линиями) нагружена силой R и жестко закреплена за основание. Аппроксимируем пластину тремя треугольными конечными элементами (КЭ) – A, B, C. Каждый КЭ соединяется с соседним только в своих вершинах – узлах. Для того чтобы это подчеркнуть, на рисунке *1 стороны некоторых треугольников искусственно отнесены друг от друга. Некоторые узлы принадлежат только одному КЭ (узлы 1 и 5), некоторые – сразу нескольким КЭ. Например, узел 2 принадлежит сразу и элементу А и элементу В; узел 3 принадлежит всем трем элементам, узел 4 – элементам В и С.

| 
|
| а)
| б)
|
Рисунок 1 – Пример разбиения пластины на конечные элементы
Предварительно рассмотрим какой-нибудь отдельный конечный элемент, например, А (рисунок 1, б). Со стороны остальных элементов и, в общем случае, со стороны внешней среды, на него действуют силы F1, F2, F3. Под действием этих сил треугольник деформируется (показано штриховыми линиями). В результате деформации вершины треугольника переместятся на малые величины, соответственно, d1, d2, d3.
Очевидно, существует связь между величинами сил и соответствующих им перемещений вершин элемента. Традиционно эта связь записывается в матричном виде:

| (1)
|
где k – т.н. матрица жесткости конечного элемента. Порядок ее получения для упругой треугольной пластины подробно рассматривается ниже. Пока же отметим, что компоненты матрицы жесткости зависят от координат вершин треугольника, толщины пластины и механических свойств материала (модуля упругости E и коэффициента Пуассона m).
Далее уравнения вида (1) для всех конечных элементов объединяют в общие матрицы – отдельно матрицу сил и отдельно в глобальную матрицу жесткости. Для этого достаточно сложить все элементы матриц конечных элементов, относящихся к одному узлу. Такой процесс называется ассемблированием.
При составлении матрицы сил силы, приложенные в одном и том же узле, но действующие от разных элементов, обозначим по имени элемента с индексом узла. Например, сила, с которой элемент В действует на 2-ой узел, равна В2, а сила, с которой элемент А действует на тот же узел, равна А2 и т.д. Заметим, что силы, с которыми элементы действуют друг на друга, по третьему закону Ньютона равны по величине, но противоположны по направлению. Например, можно записать: A2 + B2 = 0, A3+B3+C3=0, B4+C4=0. Поэтому при формировании глобальной матрицы сил существует следующее правило: если узлы (в примере 2 и 3) свободны от воздействия внешних сил и закреплений, то соответствующие этим узлам элементы глобальной матрицы сил равны нулю.
В итоге система уравнений (в матричном виде), описывающая равновесие тела под действием заданных сил и закреплений, имеет вид:

| (3)
|
где К – глобальная матрица жесткости, полученная объединением локальных матриц жесткости каждого отдельного конечного элемента; R – внешняя сила, действующая на тело; F4, F5 – силы, действующие в закреплениях.
Запрет на перемещения в узлах 4 и 5 формально можно записать, как d4=0 и d5=0. Таким образом, в итоговой системе пяти уравнений (3) остается пять неизвестных, что позволяет найти ее решение – значения перемещений di в каждом узле. Зная перемещения вершин (узлов), по формуле (1) рассчитываются силы, действующие на каждый элемент. По значениям действующих сил нетрудно рассчитать вызванные ими напряжения в каждом элементе.
Моделирование, общие понятия
Задача моделирования – исследование сложных объектов или процессов на их физических или математических моделях. Цель моделирования – найти оптимальное (наилучшее по каким-либо критериям) техническое решение. Виды моделирования:
Ø физическое;
Ø математическое;
Ø графическое (геометрическое).
При моделировании происходит замена наиболее важных свойств изучаемой системы строгими, но упрощенными по отношению к исходному природному явлению научными формулировками – моделями. Модель обеспечивает возможность точного описания и предсказания поведения системы, но только в строго ограниченной области применения — пока справедливы те исходные упрощения, на основе которых модель и строилась.
Например, при моделировании полета спутника вокруг Земли его стенки можно считать абсолютно твердым, а при моделировании столкновения того же спутника с микрометеоритом даже сверхтвердое железо можно с очень большой точностью описывать как идеальную несжимаемую жидкость. В этом парадоксальная особенность моделирования – его точность, вызванная к жизни принципиально неточными, по самой своей сущности приближенными, годными только в определенной области явлений, моделями реальной системы.
Процессы функционирования и структуру системы можно описать посредством математического моделирования. Математическое моделирование – процесс создания математической модели и действий с ней с целью получения сведений о реальной системе. Математическая модель – совокупность математических объектов и связей между ними, которая адекватно отражает важнейшие свойства системы. Математические объекты – числа, переменные, матрицы и т.п. Связи между математическими объектами – уравнения, неравенства и т.п. Любые научно-технические расчеты являются специализированными видами математического моделирования.
Система – множество закономерно связанных друг с другом элементов, образующих единую целостность, с указанием связей между ними и цели функционирования. Свойства системы отличаются от суммы свойств ее элементов. Примеры: Станок ¹ å(детали + узлы); Человек ¹ å(мозг + печень + позвоночник).




 ,
,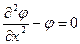 ,
,
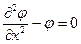

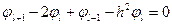 .
.
 (i=1)
(i=1) (i=2)
(i=2)













