При наложении кривых теоретических распределений на гистограмму или полигон фактического распределения, можно примерно оценить степень соответствия между ними. На практике с целью оценки рассчитываются специальные критерии, получившие название критериев согласия. Наиболее используемыми являются критерий Пирсона χ2 и критерий Колмогорова λ.
Критерий Пирсона χ2
 , где
, где
fэ и fт - соответственно частоты эмпирического и теоретического распределений
Теоретическая частота рассчитывается по формуле соответствующего теоретического распределения с учетом параметров фактического распределения.
При выравнивании по нормальному распределению рассчитывается

 - нормированное отклонение;
- нормированное отклонение;
h – величина группировочного интервала.
Критерий χ2 табулирован, то есть составлены таблицы, содержащие критическое значение критерия, превышение которого будет означать, что отклонение эмпирических частот от теоретических не случайны, следовательно, фактическое распределение не соответствует теоретическому распределению, с которым производится сравнение. Следовательно, если:
χ2ф ≤ χ2т, то изучаемое (фактическое) распределение соответствует теоретическому распределению.
Критерий Колмогорова-Смирнова

D - максимальная разность между эмпирической и теоретической частотами.
Критерий табулирован. Оценка по критерию проводится аналогично оценке по χ2.
17. Выборочное наблюдение, его виды, способы отбора.
Выборочное наблюдение – один из видов несплошного наблюдения. Преимущество выборочного наблюдения по сравнению со сплошным заключается в экономии времени, трудовых ресурсов, денежных ресурсов и появляется возможность расширить программу наблюдения. Преимущества выборочного наблюдения по сравнению с другими видами несплошного наблюдения: по результатам выборки с определенной вероятностью можно судить о генеральной совокупности.
Генеральная совокупность – совокупность, свойства которой интересуют исследователя, и из которой осуществляется отбор единиц в выборочную совокупность.
Выборочная совокупность – совокупность отобранных единиц, по которым в процессе наблюдения будут регистрироваться признаки или значения признаков.
N - объем генеральной совокупности;
n - объем выборочной совокупности.
Задача организации выборочного наблюдения – формирование репрезентативной выборки.
Виды выборки
1. Собственно-случайная выборка. Без предварительной подготовки генеральной совокупности случайно или механически из нее извлекают единицы в выборочную совокупность. В данном случае единица отбора совпадает с единицей наблюдения.
2. Стратифицированная типологическая (районированная) выборка. В генеральной совокупности выделяются типы или страты, а затем из каждого типа извлекается число единиц, пропорционально доли каждого типа в общем объеме генеральной совокупности. Единица отбора совпадает с единицей наблюдения.
3. Серийная выборка (гнездовая). В генеральной совокупности выбираются серии (гнезда) и в выборку случайно или механически производят отбор серий. Внутри серий, попавших в выборку, проводится сплошное наблюдение. Чаще всего используется для оценки качества продукции, товаров и в сельском хозяйстве.
4. Многоступенчатая выборка. Связана со сложностью социально-экономических явлений, что не позволяет на первом этапе сформировать окончательно выборочную совокупность. На каждом этапе меняется единица отбора.
5. Многофазная выборка. Каждая фаза отличается объемом программы наблюдения. Чем меньше объем выборки, тем шире программа наблюдения.
18. Cпособы отбора единиц в выборочную совокупность
1) Случайный отбор. Реализуется с использованием жеребьевки или таблиц случайных чисел.
2) Механический отбор. Частный случай случайного отбора. Реализуется через расчет шага отбора.
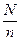 , где
, где
N – объем генеральной совокупности,
n – объем выборки.
Пример: 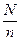 =
=  - в выборку попадает каждая пятая единица генеральной совокупности.
- в выборку попадает каждая пятая единица генеральной совокупности.
19. Средняя и предельная ошибки выборки.
Репрезентативная выборка – выборка, которая позволяет получить так называемые несмещенные оценки параметров генеральной совокупности. Выборочную совокупность можно назвать репрезентативной, если распределение единиц в выборке соответствует распределению единиц генеральной совокупности.
При проведении любого наблюдения возникают ошибки наблюдения, которые могут быть случайными и преднамеренными. При достаточно хорошей организации наблюдения этих ошибок можно избежать. При организации выборочного наблюдения возникают ошибки репрезентативности. Эти ошибки связаны не с организацией наблюдения, а с самой сутью выборочного исследования (по части, по выборочной совокупности, приходится судить о целом, о генеральной совокупности). Ошибка выборки неизбежна и состоит в том, что параметры выборочной совокупности (показатели, рассчитанные по выборке) не совпадают с параметрами (показатели генеральной совокупности). Задача исследователя: сформировать выборку, позволяющую получить минимальную ошибку и определить конкретную величину полученной ошибки. Теоретической основой определения ошибки репрезентативности являются теоремы Чебышева, Ляпунова и Бернулли.
Суть теоремы Чебышева: При неограниченном увеличении числа наблюдений в генеральной совокупности с ограниченной дисперсией с вероятностью, близкой к 1, можно утверждать, что величина ошибки выборки не превысит сколь угодно малой положительной величины ε
n → ∞,  → 1, где
→ 1, где
 - выборочная средняя;
- выборочная средняя;
 - генеральная средняя;
- генеральная средняя;
P - вероятность события, заключенного в скобках.
Суть события в том, что ошибка чрезвычайно мала.
Теорема Чебышева доказывает принципиальную возможность оценки параметров генеральной совокупности на основе выборочных данных. Исходя из этой теоремы не ясно, чему равна ошибка выборки и с какой именно вероятностью можно гарантировать непревышение конкретной величины ошибки. На эти вопросы отвечает теорема Ляпунова.
Суть теоремы Ляпунова.
При неограниченном увеличении числа наблюдений в генеральной совокупности с ограниченной дисперсией вероятность того, что ошибка выборки не превысит величины, равна нормированной функции Лапласа.
n → ∞, 
 , где
, где
μ- средняя ошибка выборки.
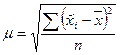 , где
, где
 - средняя выборочная по i-ой выборке.
- средняя выборочная по i-ой выборке.
n - число выборок.
Данная формула на практике не может быть использована, так как неизвестна величина генеральной средней и фактически проводится всегда лишь одна выборка.
Математической статистикой доказано, что μ2 прямо пропорциональна дисперсии генеральной совокупности и обратно пропорциональна объему выборки.
 , где
, где
σ2 – генеральная дисперсия.
Между величинами выборочной и генеральной дисперсий существует зависимость:
 , где
, где
S2 – выборочная дисперсия.
При большом объеме выборки сомножитель 
Поэтому на практике его игнорируют и в расчете средней ошибки используют величину выборочной дисперсии.

t·μ = Δ - предельная ошибка выборки.
 - нормированное отклонение
- нормированное отклонение
 - нормированное отклонение выборочной средней от генеральной среденей.
- нормированное отклонение выборочной средней от генеральной среденей.
Теорема Ляпунова доказывает, что при большом объеме выборки распределение ошибки выборки подчинено закону нормального распределения.
Для нормального распределения составлены таблицы, в которых зафиксировано отношение t и уровня вероятности.
Задавая уровень вероятности, по таблицам находится соответствующее значение нормированного отклонения. Социально-экономические исследования чаще всего проводятся с вероятностью p = 0.954, t = 1.96 ≈ 2
p = 0.997, t ≈ 3.
Если задана p = 0.954, то Δ = 2·μ
Доверительный интервал: 
В условиях большой выборки распределение ошибки выборки подчиняется закону нормального распределения. Поэтому, задавая уровень вероятности, величину t (значение нормированного отклонения) находят по таблице нормированной функции Лапласа.
Выше указанные формулы расчета ошибки выборки разработаны для повторного отбора. В статистике понятие повторного и бесповторного отбора соответствует понятиям возвратного и безвозвратного шара в теории вероятности. Повторный отбор заключается в том, что единица генеральной совокупности, изъятая в выборку, возвращается назад в генеральную совокупность и может быть повторно выбрана в выборочную совокупность. Бесповторный отбор – отобранная из генеральной совокупности единица не возвращается назад.
При повторном отборе на протяжении всего отбора сохраняется неизменная вероятность попадания единицы в выборку p = 1/N
При бесповторном отборе вероятность изменения от  для первой единицы отбора до
для первой единицы отбора до  для последней единицы отбора.
для последней единицы отбора.
Поэтому формула средней ошибки выборки для бесповторного отбора, который, как правило, используется в анализе социально-экономических явлений, имеет вид
20. Влияние вида выборки и способа отбора на величину ошибки выборки
Ошибка выборки есть всегда, это связано с самой сутью выборочного наблюдения. Величина ошибки выборки зависит также от вида выборки. В формуле средней ошибки при реализации различных видов выборки используются разные дисперсии.
При проведении любого наблюдения возникают ошибки наблюдения, которые могут быть случайными и преднамеренными. При достаточно хорошей организации наблюдения этих ошибок можно избежать. При организации выборочного наблюдения возникают ошибки репрезентативности. Эти ошибки связаны не с организацией наблюдения, а с самой сутью выборочного исследования (по части, по выборочной совокупности, приходится судить о целом, о генеральной совокупности). Ошибка выборки неизбежна и состоит в том, что параметры выборочной совокупности (показатели, рассчитанные по выборке) не совпадают с параметрами (показатели генеральной совокупности). Задача исследователя: сформировать выборку, позволяющую получить минимальную ошибку и определить конкретную величину полученной ошибки. Теоретической основой определения ошибки репрезентативности являются теоремы Чебышева, Ляпунова и Бернулли
21. Определение доверительных интервалов для генеральной средней и генеральной доли.
Теорема Бернулли – это частный случай теоремы Чебышева и теоремы Ляпунова. Она является основой расчета ошибки выборки для доли. То есть при изучении альтернативного признак или так называемой дихотомической переменной (имеющей всего два исхода). Реально это оценивается в расчете доли единиц совокупности, обладающих или не обладающих данным признаком.
При расчете средней ошибки доли используется формула, аналогичная средней ошибке средней величины, но с учетом дисперсии доли.
 , где
, где
W - выборочная совокупность (доля);
p - доля генеральной совокупности.
σ2 = W · (1 – W) - дисперсия доли.
W – tμ ≤ p ≤ W + tμ
Между величинами выборочной и генеральной дисперсий существует зависимость:
 , где
, где
S2 – выборочная дисперсия.
При большом объеме выборки сомножитель 
Поэтому на практике его игнорируют и в расчете средней ошибки используют величину выборочной дисперсии.

t·μ = Δ - предельная ошибка выборки.
 - нормированное отклонение
- нормированное отклонение
 - нормированное отклонение выборочной средней от генеральной среденей.
- нормированное отклонение выборочной средней от генеральной среденей.
Теорема Ляпунова доказывает, что при большом объеме выборки распределение ошибки выборки подчинено закону нормального распределения.
Для нормального распределения составлены таблицы, в которых зафиксировано отношение t и уровня вероятности.
Задавая уровень вероятности, по таблицам находится соответствующее значение нормированного отклонения. Социально-экономические исследования чаще всего проводятся с вероятностью p = 0.954, t = 1.96 ≈ 2
p = 0.997, t ≈ 3.
Если задана p = 0.954, то Δ = 2·μ
Доверительный интервал: 
В условиях большой выборки распределение ошибки выборки подчиняется закону нормального распределения. Поэтому, задавая уровень вероятности, величину t (значение нормированного отклонения) находят по таблице нормированной функции Лапласа.
22. Расчет объема выборки.
На стадии проектирования выборочного наблюдения рассчитывается объем выборки, который позволит получить допустимую величину ошибки, то есть ошибку, которая удовлетворит задачам исследования. Расчет объема выборки осуществляют исходя из формулы ошибки выборки. Предельная ошибка выборки:
 ,
,  ,
, 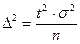 ,
, 
Величина ошибки выборки обусловлена задачами исследования и задается на стадии проектирования.
Значение t зависит от устанавливаемого уровня вероятности. Значение дисперсии берется по результатам предшествующих аналогичных исследований, если таковые проводились и если за время между исследованиями не произошло существенных изменений в изучаемой совокупности.
Может быть проведено пробное исследование и по результатам его рассчитана величина дисперсии. Но очень часто нет средств на проведение пилотажного (пробного) исследования.
К определению дисперсии подходят формально, исходя их привила трех σ - когда невозможно провести пилотажные исследования.
σ = 1/6 R, где R – размах вариации.
Если распределение заведомо асимметрично, то значение σ = 1/5 R
В формуле расчета объема выборки ( ) ошибка выборки берется как
) ошибка выборки берется как
абсолютная величина, однако, на практике размер ошибки задается, как правило, как относительная величина. То есть говорят, что ошибка не должна превышать 2% (или 5%).
 →
→ 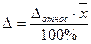

23. Малая выборка: понятие, особенности.
При использовании больших выборок, сформированных из больших генеральных совокупностей, величина ошибки выборки подчиняется нормальному закону, который устанавливает связь между величиной вероятности и значением t.

Если анализируемая выборка малого объема, то распределение ошибок выборки не подчиняется нормальному закону распределения. Поэтому проблема малой выборки длительное время оставалась нерешенной.
Проблема малой выборки была решена английским математиком и статистиком по фамилии Госсет, который вошел в историю под псевдонимом Стьюдент.
1908 г – доказал, что распределение ошибок в условиях малой выборки подчиняется особому закону распределения, который и получил его имя – t-распределение Стьюдента.
Распределение Стьюдента, как и нормальное распределение, симметрично, однако ветви кривой распределения Стьюдента медленнее приближаются к оси абсцисс. То есть вероятность появления больших отклонений от средней величины в распределении Стьюдента выше, чем в нормальном распределении.

По t-распределению Стьюдента составлены таблицы, в которых (в отличии от нормального распределения) вероятность связана не только с величиной t, но и с числом степеней свободы, которое определяется
d.f. = n – 1 (n – объем совокупности)
При объеме выборки n ≥ 100 значения в таблицах нормального распределения и распределения Стьюдента полностью совпадают, при 30 ≤ n ≤ 100 - расхождения незначительные, при n < 30 - существенные расхождения.
Безусловно малой выборкой считается выборка объемом меньше 30 единиц. Поэтому при работе с выборками таких объемов в формуле предельной ошибки выборки используется величина t из таблицы t-распределения Стьюдента.
В формуле расчета средней ошибки выборки мы не можем игнорировать сомножитель, корректирующий величину выборочной дисперсии.
 - в условиях малой выборки
- в условиях малой выборки
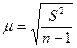 , где
, где
S - выборочная дисперсия.
То есть дисперсия делится не на объем выборки, а на число степеней свободы.
24. Проверка существенности различий между выборочными средними
Проверка различий осуществляется на основе t- статистики.ьПроверка нулевой гипотезы Но:
 ,
,
где выборочная средняя первой выборки равна средней по второй выборке

Проверка на основе t-статистики означает оценку отношений оцениваемой величины к стандартной ошибке.
 , где
, где
 , среднеквадратичная ошибка
, среднеквадратичная ошибка
Оценка генеральной дисперсии по двум выборкам 

Оценка гипотезы по результатом расчетов t-статистики:
Если tрасч.< tтабл, то принимается нулевая гипотеза о равенстве средних величин, то есть расхорждение между ними случайно,
Если tрасч.> tтабл, то гипотеза отвергается, выборочные средние не равны, расхождение неслучайно.
25. Виды связей: функциональная, статистическая, корреляционная.
Все в этом мире взаимосвязано. Чтобы управлять социально-экономическими процессами и явлениями, необходимо знать наличие, направленность, силу связи между явлениями или признаками.
Существуют два вида связей:



 , где
, где
 - нормированное отклонение;
- нормированное отклонение;
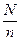 , где
, где - в выборку попадает каждая пятая единица генеральной совокупности.
- в выборку попадает каждая пятая единица генеральной совокупности. → 1, где
→ 1, где - выборочная средняя;
- выборочная средняя; - генеральная средняя;
- генеральная средняя;
 , где
, где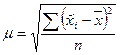 , где
, где , где
, где , где
, где

 - нормированное отклонение выборочной средней от генеральной среденей.
- нормированное отклонение выборочной средней от генеральной среденей.
 для первой единицы отбора до
для первой единицы отбора до  для последней единицы отбора.
для последней единицы отбора. , где
, где ,
,  ,
, 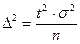 ,
, 
 →
→ 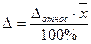



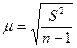 , где
, где ,
,
 , где
, где , среднеквадратичная ошибка
, среднеквадратичная ошибка




