1.Система аксиом Колмогорова непротиворечива, так как существуют реальные объекты, которые удовлетворяют одновременно всем аксиомам Колмогорова.
2. Система аксиом Колмогорова неполна. Это значит, что даже при одном множестве элементарных событий U вероятности на множестве F могут быть выбраны многими различными способами.
Неполнота системы аксиом Колмогорова не является недостатком, а, наоборот, обеспечивает ее возможность её широкого практического применения, так как позволяет в разных задачах рассматривать одинаковые множества случайных событий с различными вероятностями. Это можно проиллюстрировать известным парадоксом Бертрана. Пусть для некоторой окружности случайным образом выбирается хорда. Найти вероятность того, что эта хорда длиннее стороны правильного треугольника, вписанного в данную окружность. Бертран утверждает, что эта вероятность определяется неоднозначно, т. e. различные методы приводят к разным результатам.
21.Классическое определение вероятности случайного события
Под вероятностью случайного события в математике понимают меру возможности осуществления данного события в конкретных условиях эксперимента (испытания).
Рассмотрим некоторую конечную полную группу равновоз-можных элементарных событий (исходов) В,, В2,..., Вп, т. е. совокупность всех единственно возможных, несовместных и вместе с тем равновозможных результатов некоторого испытания, причем пусть интересующее нас случайное событие А осуществляется тогда и только тогда, когда наступают некоторые из элементарных событий указанной полной группы. Пусть таких событий, благоприятствующих для события А, насчитывается т (естественно, т<п). Тогда вероятность события А определяют следующим образом:
Определение. Вероятностью Р(А) случайного события А называется отношение количества т элементарных событий, благо-приятствующих событию А, к общему количеству элементарных событий п:
P*(A)=m/n
Поскольку в общем случае 0 < т < п, то из этого определения, называемого классическим определением вероятности случайного события, следует, что вероятность произвольного случайного события принадлежит отрезку [0,1], т.е.
0≤ Р(А)≤1
Классическое определение вероятности. Если при испытаниях нет каких-либо причин, вследствие которых одно случайноесобытие появлялось бы чаще других (равновозможные события), можно определить вероятность исходя из теоретических соображений. Например, выясним в случае бросания монеты частоту выпадания герба (событие А). Разными экспериментаторамипри нескольких тысячах испытаний было показано, что относительная частота такого события принимает значения, близкие к0,5. Учитывая, что появление герба и противоположной стороны монеты (событие В) являются событиями равновозможными, если монета симметрична, суждение Р(А) = Р(В) = 0,5 можно было бы сделать и без определения частоты этих событий. На основе понятия «равновозможности» событий формулируется другое определение вероятности.
Допустим, что в результате испытания должно произойти только одно из п равновозможных несовместных событий (несовместными называют события, если их одновременное осуществление невозможно). Пусть рассматриваемое событие А происходит в т случаях, которые называются благоприятствующими А, ине происходит при остальных п - т, неблагоприятствующих А. Тогда вероятностью можно назвать отношение благоприятствующих случаев к общему числу равновозможных несовместных событий:
Р(А) = m/n
22. Статистической вероятностью события А называется относительная частота появления этого события в произведённых испытаниях:
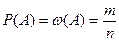
где 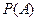 – вероятность появления события А;
– вероятность появления события А;
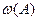 – относительная частота появления события А;
– относительная частота появления события А;
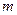 - число испытаний, в которых появилось событие А;
- число испытаний, в которых появилось событие А;
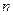 - общее число испытаний.
- общее число испытаний.
В отличие от классической вероятности статистическая вероятность является характеристикой опытной, экспериментальной.
Пример: Для контроля качества изделий из партии наугад выбрано 100 изделий, среди которых 3 изделия оказались бракованными. Определить вероятность брака.
 .
.
Статистический способ определения вероятности применим лишь к тем событиям, которые обладают следующими свойствами:
· Рассматриваемые события должны быть исходами только тех испытаний, которые могут быть воспроизведены неограниченное число раз при одном и том же комплексе условий.
· События должны обладать статистической устойчивостью (или устойчи- востью относительных частот). Это означает, что в различных сериях испытаний относительная частота события изменяется незначительно.
· Число испытаний, в результате которых появляется событие А, должно быть достаточно велико.
ОПРЕДЕЛЕНИЕ (статистическим определением вероятности). Число, к которому стремится устойчивая относительная частота, называется статистической вероятностью этого события. 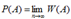
Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р (А + В) = Р (А) + Р (В). Доказательство
С л е д с т в и е. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р (A1 + A2 +... + An) = Р (A1) + Р (A2) +... + Р (An).
23. Геометрическое определение вероятности
Пусть случайное испытание можно представить себе как бросание точки наудачу в некоторую геометрическую область G (на прямой, плоскости или пространстве). Элементарные исходы – это отдельные точки G, любое событие – это подмножество этой области, пространства элементарных исходов G. Можно считать, что все точки G «равноправны» и тогда вероятность попадания точки в некоторое подмножество пропорционально его мере (длине, площади, объему) и не зависит от его расположения и формы.
Геометрическая вероятность события А определяется отношением:
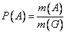 ,
,
где m(G), m(A) – геометрические меры (длины, площади или объемы) всего пространства элементарных исходов и события А.
24.

Два события называются совместными в данном опыте, если появление одного из них не исключает появление другого события.
Пример 10. Два стрелка делают по одному выстрелу в мишень. Событие 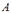 - попадание 1-го стрелка в мишень и событие
- попадание 1-го стрелка в мишень и событие 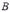 - попадание 2-го стрелка в мишень. Эти события совместные, так как возможна ситуация, когда оба стрелка попадут в мишень.
- попадание 2-го стрелка в мишень. Эти события совместные, так как возможна ситуация, когда оба стрелка попадут в мишень.
Два события называются несовместными в данном опыте, если появление одного из них е исключает появление другого события.





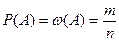
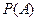 – вероятность появления события А;
– вероятность появления события А;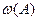 – относительная частота появления события А;
– относительная частота появления события А;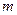 - число испытаний, в которых появилось событие А;
- число испытаний, в которых появилось событие А;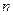 - общее число испытаний.
- общее число испытаний. .
.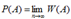
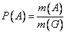 ,
, 
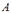 - попадание 1-го стрелка в мишень и событие
- попадание 1-го стрелка в мишень и событие 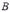 - попадание 2-го стрелка в мишень. Эти события совместные, так как возможна ситуация, когда оба стрелка попадут в мишень.
- попадание 2-го стрелка в мишень. Эти события совместные, так как возможна ситуация, когда оба стрелка попадут в мишень.


