Комбинационные логические цепи

Основные положения алгебры логики

Анализ и синтез логических схем осуществляется на базе аппарата алгебры логики или булевой алгебры [9]. Излагать весь аппарат не имеет смысла, так как в инженерной практике используются два-три закона алгебры логики.

В алгебре логики переменные могут принимать только два значения, 0 или 1. Для двух аргументов существуют 16 логических функций (операций, логических действий). Над переменными в основном производятся три логических действия: сложение, умножение, отрицание (инверсия), что соответствует функциям ИЛИ, И, НЕ. Все функции в булевой алгебре могут быть описаны с помощью таблицы истинности. В нижеследующих таблицах описаны функции И(f1), ИЛИ(f2),НЕ(f3).

Аргументы		Функции
x2	x1	f1	f2
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	1

 

Аргумент	Функция
x	f3
0	1
1	0

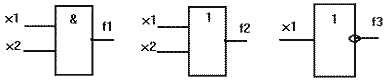Вместо функции И часто используется термин "конъюнкция", вместо функции ИЛИ - термин "дизъюнкция". По ЕСКД логические элементы, реализующие функции И(f1), ИЛИ(f2), НЕ(f3), изображаются так, как представлено на рисунке.

При написании логических формул для функции И используются следующие знаки : &, U, точка или ее отсутствие; для функции ИЛИ +,^. Функция НЕ обозначается штрихом над аргументом. Мы для обозначения отрицания будем использовать апостроф. Таким образом, можно записать:

f1 = x2&x1 = x2^x1 = x2x1f2 = x2Ux1 = x2+x1 f3 = x'

Основные законы алгебры Буля

Как уже отмечалось, в булевой алгебре все операции осуществляются с логическими переменными и подчиняются законам алгебры логики. Опишем некоторые из них.

а) Переместительный закон а + в = в + а; ав = ваб) Сочетательный закон (а + в) + с = а + (в + с); (ав)с = а(вс)в) Распределительный закон а(в + с) = ав + ас; а + вс = (а + в)(а + с)г) Закон поглощения а + ав = а(1 + в) = а; а(a + в) = а + ав = ад) Закон склеивания ав + ав' = а; (а + в)(а + в') = ае) Идемпотентный закон a + a = a; a & a = aё) Правила де Моргана Эти правила справедливы для любого числа аргументов.      а + в + с + .... + z = ( а'в'с'...z' )' авс... = ( а' + в' + с' + ... + z' )'

Эти правила можно описать таким алгоритмом.

Для перехода от логической суммы к логическому произведению необходимо проделать следующие операции :

1. проинвертировать все слагаемые в отдельности;

2. заменить знаки дизъюнкции на знаки конъюнкции;

3. проинвертировать получившееся выражение.

Аналогично выполняется переход от логического произведения к логической сумме.В инженерной практике используются лишь правила де Моргана и закон склеивания(в виде карт Карно).

Кроме основных функций И, ИЛИ, НЕ в алгебре логики часто используются функции равнозначности (эквивалентности) и неравнозначности (сумма по модулю 2 ).

Для обозначения этих функций используются следующие знаки : равнозначность - ~ , сумма по модулю 2 - . Содержание этих функций отражено в таблице .

a	b	f4	f5
0	0	1	0
0	1	0	1
1	0	0	1
1	1	1	0

Из таблицы получаем:

f4 = а ~ в = а'в' + авf5 = a  в = а'в + ав'Из таблицы видно, что f4 = f5' или f5 = f4'Таким образом,а'в' + ав = ( ав' + а'в )' , или а~в = ( а в )' , а в = (а~в)'

Синтез комбинационных схем

Синтез комбинационных схем можно проиллюстрировать решением простой задачи.

Задача 1

Приёмная комиссия в составе трех членов комиссии и одного председателя решает судьбу абитуриента большинством голосов. В случае равного распределения голосов большинство определяется той группой, в которой оказался председатель приемной комиссии. Построить автомат, обеспечивающий определение большинства голосов.

Решение

Пусть f - функция большинства голосов. f = 1, если большинство членов комиссии проголосовало за приём абитуриента, и f = 0 в противном случае.

Обозначим через x4 голос председателя комиссии. x4 = 1, если председатель комиссии проголосовал за приём абитуриента. x3, x2, x1 - голоса членов приёмной комиссии.

С учётом вышеуказанных допущений условие задачи можно однозначно представить в виде таблицы истинности.

Заполнение таблицы осуществляем с учётом того, что функция f является полностью определённой, т.е. она определена на всех возможных наборах переменных x1 - x4. Для n входных переменных существует N = 2n наборов переменных. В нашем примере N = 24 = 16 наборов.

Записывать эти наборы можно в любом порядке, но лучше в порядке возрастания двоичного кода.

x4 x3 x2 x1 f0 0 0 0 00 0 0 1 00 0 1 0 00 0 1 1 0 0 1 0 0 00 1 0 1 0 0 1 1 0 00 1 1 1 11 0 0 0 01 0 0 1 1 1 0 1 0 11 0 1 1 11 1 0 0 11 1 0 1 11 1 1 0 11 1 1 1 1

Примечание

Здесь и далее под набором будем понимать конъюнкцию всех входных переменных. Существует множество научных определений для набора(конституента,терм,импликанта,минтерм и т.д.),но они только вносят путаницу.

Все наборы, на которых функция принимает значение 1 , будем называть единичными, или рабочими. Наборы, на которых функция принимает значение 0, будем называть нулевыми, или запрещенными.

Для того, чтобы по таблице истинности найти функцию f, достаточно выписать все единичные наборы и соединить их знаком дизъюнкции.

Таким образом,

f = x4'x3x2x1 + x4x3'x2'x1 + x4x3'x2x1' + x4x3'x2x1 + x4x3x2'x1' + x4x3x2'x1 +     + x4x3x2x1' + x4x3x2x1

Полученная форма функции называется совершенной дизъюнктивной нормальной формой (СДНФ), так как каждое логическое слагаемое представляет собой конъюнкцию всех аргументов.

Очевидно, применяя основные законы булевой алгебры, мы могли бы аналитически уменьшить сложность полученного выражения. Но это наихудший способ минимизации булевых функций. Покажем это на предыдущем примере. Представим полученную функцию в виде логической суммы цифровых рабочих наборов:

f = 0111+1001+1010+1011+1100+1101+1110+1111 =   = (0111+1111)+(1001+1011)+(1010+1011)+(1100+1101)+(1110+1111) =   = -111+10-1+101-+110-+111- = -111+10-1+(101-+111-)+(110-+111-) =   = -111+10-1+1-1-+11- = x3x2x1+ x4x3'x1+ x4x2+ x4x3.

Как мы потом увидим, результат минимизации должен быть компактнее. Но при аналитической минимизации придётся ввести неочевидную группировку: (1101+1111).

f = 0111+1001+1010+1011+1100+1101+1110+1111 =   =(0111+1111)+(1001+1011)+(1010+1011)+(1100+1101)+(1110+1111) + (1101+1111).=   = -111+10-1+101-+110-+111-+11-1 = -111+(10-1+11-1)+(101-+111-)+(110-+111-) =   = -111+1-1+1-1-+11- = x3x2x1+ x4x1+ x4x2+ x4x3 = x3x2x1+ x4 (x1+ x2+ x3).

После длинных и неочевидных группировок удалось, наконец, получить правильное решение. При числе аргументов более 4-х аналитический метод минимизации не рационален.