5.3.1. Задача №1
Построить многочлен Лагранжа, интерполирующий профиль высот  на участке нефтепровода.
на участке нефтепровода.
Данные по вариантам:
1.

| 180
| 180.1
| 180.2
| 180.3
| 180.4
|

| 56.2
| 54.2
| 54.9
| 53.2
| 53.5
|
2.

| 180.6
| 180.7
| 180.8
| 180.9
| 181
|

| 55.6
| 54.2
| 57.1
| 56.0
| 54.3
|
3.

| 181.1
| 181.2
| 181.3
| 181.4
| 181.5
|

| 52.3
| 53.4
| 53.0
| 53.9
| 55.7
|
4.

| 181.6
| 181.7
| 181.8
| 181.9
| 182
|

| 57.0
| 56.8
| 57.0
| 55.1
| 54.5
|
5.

| 182.1
| 182.2
| 182.3
| 182.4
| 182.5
|

| 53.6
| 50.0
| 55.5
| 55.3
| 60.7
|
6.

| 182.6
| 182.7
| 182.8
| 182.9
| 183
|

| 62.2
| 64.4
| 65.0
| 64.0
| 65.2
|
7.

| 183.1
| 183.2
| 183.3
| 183.4
| 183.5
|

| 63.6
| 65.0
| 66.2
| 62.1
| 58.0
|
8.

| 183.6
| 183.7
| 183.8
| 183.9
| 184
|

| 61.2
| 64
| 61.5
| 63.5
| 62.1
|
9.

| 184.1
| 184.2
| 184.3
| 184.4
| 184.5
|

| 64.4
| 66.2
| 63.5
| 65.4
| 62.4
|
10.

| 184.6
| 184.7
| 184.8
| 184.9
| 185
|

| 65.7
| 67.2
| 66.5
| 63.0
| 63.2
|
11.

| 181.2
| 181.3
| 181.4
| 181.5
| 181.6
|

| 52.3
| 54.8
| 53.0
| 53.1
| 55.7
|
12.

| 184.1
| 184.2
| 184.3
| 184.4
| 184.5
|

| 55.3
| 53.4
| 53.0
| 53.4
| 55.5
|
13.

| 185.1
| 185.2
| 185.3
| 185.4
| 185.5
|

| 62.4
| 63.1
| 63.0
| 58.9
| 59.0
|
14.

| 185.5
| 185.6
| 185.7
| 185.8
| 185.9
|

| 61.2
| 64
| 61.5
| 63.5
| 62.1
|
15.

| 186.6
| 186.7
| 186.8
| 186.9
| 187
|

| 62.2
| 64.4
| 65.0
| 64.0
| 65.2
|
16.

| 187
| 187.1
| 187.2
| 187.3
| 187.4
|

| 56.2
| 54.2
| 54.9
| 53.2
| 53.5
|
17.

| 187.1
| 187.2
| 187.3
| 187.4
| 187.5
|

| 52.3
| 53.4
| 53.0
| 53.9
| 55.7
|
18.

| 187.6
| 187.7
| 187.8
| 187.9
| 188
|

| 63.6
| 65.0
| 66.2
| 62.1
| 58.0
|
19.

| 188.0
| 188.1
| 188.2
| 188.3
| 188.4
|

| 61.2
| 64
| 61.5
| 63.5
| 62.1
|
20.

| 188.6
| 188.7
| 188.8
| 188.9
| 189
|

| 64.4
| 66.2
| 63.5
| 65.4
| 62.4
|
21.

| 189.6
| 189.7
| 189.8
| 189.9
| 190
|

| 55.6
| 54.2
| 57.1
| 56.0
| 54.3
|
22.

| 190.1
| 190.2
| 190.3
| 190.4
| 190.5
|

| 63.6
| 65.0
| 66.2
| 62.1
| 58.0
|
23.

| 190.6
| 190.7
| 190.8
| 190.9
| 191
|

| 57.0
| 56.8
| 57.0
| 55.1
| 54.5
|
24.

| 191.1
| 191.2
| 191.3
| 191.4
| 191.5
|

| 64.4
| 66.2
| 63.5
| 65.4
| 62.4
|
5.3.2. Задача №2
Известно, что использование кислот соляной  и кремнефтористоводородной
и кремнефтористоводородной 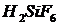 , благодаря растворению терригенных коллекторов, углубляет и развивает сеть каналов. Но одновременно и ограничивает приток пластовых вод к скважине за счет закупорки фильтрационных каналов в водоносном пласте осадками кремнефторидов.
, благодаря растворению терригенных коллекторов, углубляет и развивает сеть каналов. Но одновременно и ограничивает приток пластовых вод к скважине за счет закупорки фильтрационных каналов в водоносном пласте осадками кремнефторидов.
Проблемы поиска оптимального режима обработки призабойной зоны с целью снижения пластовых потерь нефти приводят к необходимости исследования зависимости количества выпадающего осадка от свойств пластовой воды.
В таблице приведены результаты эксперимента по смешиванию 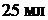 пластовой воды при температуре
пластовой воды при температуре  с кремнефтористоводородной кислотой
с кремнефтористоводородной кислотой 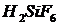 с последующей фильтрацией полученого раствора.
с последующей фильтрацией полученого раствора.
плотность пласт. воды,
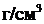
| 1.05
| 1.12
| 1.13
| 1.14
| 1.15
| 1.16
| 1.17
|
| содержание осадка, %
(весовое)
| 8.4
| 14.2
| 14.4
| 15.4
| 19.7
| 20.6
| 22.6
|
Необходимо построить зависимость процентного содержания осадка, получающегося при смешивании пластовой воды с кислотой 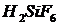 , от плотности пластовой воды. Для построения зависимости воспользоваться многочленом Лагранжа.
, от плотности пластовой воды. Для построения зависимости воспользоваться многочленом Лагранжа.
5.3.3. Задача №3
Построить интерполяционный многочлен Лагранжа для зависимости растворимости кварцевого песка в смеси двух кислот (20 % - ной кислоты 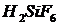 и кислоты
и кислоты  ) от процентного содержания кислоты
) от процентного содержания кислоты  в смеси.
в смеси.
Данные измерений для отдельных смесей приведены в таблице. Они были получены при температуре  для
для 
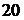 грамм песка и при объеме кислотного раствора
грамм песка и при объеме кислотного раствора 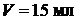 .
.
| состав раствора
| 20 % 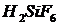 +0 %
+0 % 
| 20 % 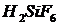 +5 %
+5 % 
| 20 % 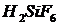 +10 %
+10 % 
| 20 % 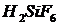 +15 %
+15 % 
|
| раствори-мость песка, г/л
|
12.04
|
31.85
|
33.9
|
37.8
|
6. Численное интегрирование
6.1. Основные определения
Методы численного интегрирования используются в тех случаях, когда необходимо найти значение определенного интеграла вида  , но аналитически посчитать его значение не представляется возможным из-за сложного вида подынтегральной функции. Известно, что значение определенного интеграла равно
, но аналитически посчитать его значение не представляется возможным из-за сложного вида подынтегральной функции. Известно, что значение определенного интеграла равно 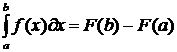 , где
, где 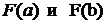 – значения первообразной
– значения первообразной 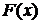 для подынтегральной функции
для подынтегральной функции 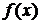 в точках
в точках 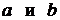 соответственно. Например,
соответственно. Например, 
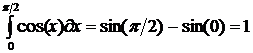 . Но далеко не для всякой функции
. Но далеко не для всякой функции 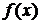 легко указать
легко указать 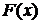 , как это сделано в примере. Тогда прибегают к численному интегрированию.
, как это сделано в примере. Тогда прибегают к численному интегрированию.
Есть еще, правда, способ подсчета значения интеграла путем предварительного представления подынтегральной функции в виде степенного ряда Тейлора и последующего интегрирования многочлена, представляющего несколько первых членов этого ряда. Но этот способ мы здесь рассматривать не будем. А рассмотрим находящие наибольшее применение методы численного интегрирования.
Вспомним некоторые понятия, необходимые для дальнейшего изложения.
Пусть на отрезке 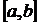 задана функция
задана функция 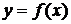 . С помощью точек
. С помощью точек 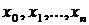 разобьем отрезок
разобьем отрезок 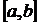 на
на  отрезков
отрезков 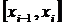 (
(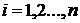 ), причем
), причем  . На каждом из этих отрезков выберем произвольную точку
. На каждом из этих отрезков выберем произвольную точку  и найдем произведение значения функции в этой точке
и найдем произведение значения функции в этой точке 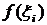 на длину отрезка
на длину отрезка 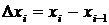 :
:
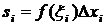 .
.
Составим сумму таких произведений:

Сумма  называется интегральной суммой. Определенным интегралом от функции
называется интегральной суммой. Определенным интегралом от функции 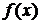 на отрезке
на отрезке 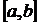 называется предел интегральной суммы при неограниченном увеличении числа точек разбиения и стремлении к нулю длины наибольшего отрезка разбиения:
называется предел интегральной суммы при неограниченном увеличении числа точек разбиения и стремлении к нулю длины наибольшего отрезка разбиения:

Известно, если
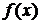
непрерывна на отрезке
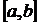
, то предел интегральной суммы существует и не зависит от способа разбиения отрезка
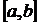
и выбора точек
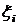
.
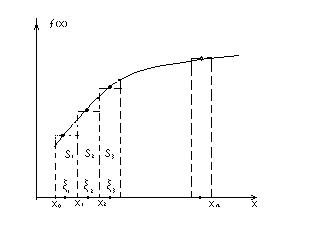
Рис. 1
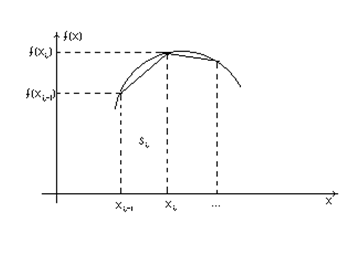
Геометрический смысл введенных понятий для случая  0 проиллюстрирован на рисунке 1. Величины
0 проиллюстрирован на рисунке 1. Величины 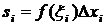 представляют из себя площади прямоугольников, отмеченных пунктирной линией, а сама интегральная сумма – площадь ступенчатой фигуры, образуемой этими прямоугольниками. При стремлении же к нулю длин отрезков разбиения площадь этой ступенчатой фигуры стремится к площади фигуры, заключенной под кривой
представляют из себя площади прямоугольников, отмеченных пунктирной линией, а сама интегральная сумма – площадь ступенчатой фигуры, образуемой этими прямоугольниками. При стремлении же к нулю длин отрезков разбиения площадь этой ступенчатой фигуры стремится к площади фигуры, заключенной под кривой 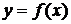 . Это и есть значение интеграла.
. Это и есть значение интеграла.
Используют следующие методы численного интегрирования.
6.1.1. Метод прямоугольников.
В этом методе непосредственно заменяют значение определенного интеграла интегральной суммой, разбивая обычно отрезок интегрирования на  равных по длине отрезков. Тогда
равных по длине отрезков. Тогда  , являющуюся длиной отрезка разбиения, называют шагом разбиения. В качестве
, являющуюся длиной отрезка разбиения, называют шагом разбиения. В качестве 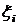 могут выбираться левые (
могут выбираться левые ( ) или правые (
) или правые ( ) границы отрезков разбиения или их середины (
) границы отрезков разбиения или их середины (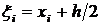 ). Получают следующие формулы метода прямоугольников, отвечающие этим трем способам выбора точек
). Получают следующие формулы метода прямоугольников, отвечающие этим трем способам выбора точек 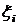 :
:
а) Формула левых прямоугольников
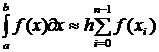
б) Формула правых прямоугольников
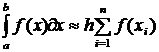
в) Формула средних прямоугольников
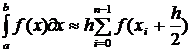
Главные члены погрешностей этих формул равны соответственно:
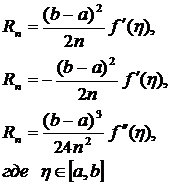
6.1.2. Метод трапеций
В этом методе применяют линейную интерполяцию интегрируемой функции, т.е. график функции 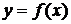 представляют в виде ломаной, соединяющей точки
представляют в виде ломаной, соединяющей точки 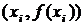 . В этом случае площадь под кривой на каждом отрезке разбиения заменяется площадью под прямой, которая равна площади прямоугольной трапеции с высотой
. В этом случае площадь под кривой на каждом отрезке разбиения заменяется площадью под прямой, которая равна площади прямоугольной трапеции с высотой 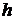 и основаниями
и основаниями  , т.е.
, т.е. 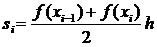 . Получается формула трапеций
. Получается формула трапеций
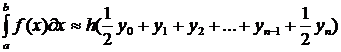 ,
,
где
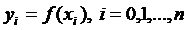
.
Рис. 2
Главный член погрешности этой формулы равен:
 .
.
6.1.3. Метод Симпсона
В этом методе отрезок интегрирования 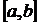 разбивается на четное число
разбивается на четное число  равных частей с шагом
равных частей с шагом 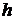 . На каждом отрезке
. На каждом отрезке 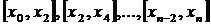 подынтегральная функция заменяется интерполяционным многочленом второй степени:
подынтегральная функция заменяется интерполяционным многочленом второй степени: 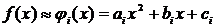

В качестве  можно принять интерполяционный многочлен Лагранжа второй степени, график которого проходит через точки
можно принять интерполяционный многочлен Лагранжа второй степени, график которого проходит через точки  , где
, где 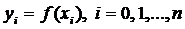 .
.
В этом случае площадь под кривой на каждом отрезке 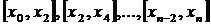 заменяется площадью под параболой, а эту площадь легко посчитать, т.к. первообразная квадратичной функции известна:
заменяется площадью под параболой, а эту площадь легко посчитать, т.к. первообразная квадратичной функции известна:
для

ее первообразной будет

.
Рис. 3
Сумма же этих площадей дает нам приближенное значение интеграла. Формула метода Симпсона имеет вид:
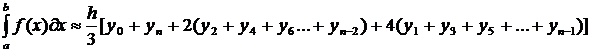 Главный член погрешности этой формулы равен:
Главный член погрешности этой формулы равен:
 .
.
Надо упомянуть об одном практическом аспекте в вычислении интегралов. Обычно требуется вычислить интеграл  с заданной точность
с заданной точность 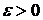 , т.е. получить такое приближенное значение его
, т.е. получить такое приближенное значение его  , чтобы выполнялось
, чтобы выполнялось 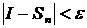 .
.
Удовлетворить этому требованию можно, либо выбрав число  разбиения отрезка интегрирования так, чтобы главный член погрешности по модулю был меньше
разбиения отрезка интегрирования так, чтобы главный член погрешности по модулю был меньше  , либо воспользовавшись следующим приемом.
, либо воспользовавшись следующим приемом.
Посчитать значение интеграла для некоторого 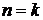 . Затем сделать такие же расчеты для
. Затем сделать такие же расчеты для  . Затем сравнить полученные результаты. Если окажется, что
. Затем сравнить полученные результаты. Если окажется, что 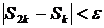 , то считать точность достигнутой и принять
, то считать точность достигнутой и принять  . Если же условие не выполняется, то вновь удвоить число разбиений отрезка и сравнить два последних приближения так, как это было предложено выше. Закончить процесс при выполнении указанного условия и последнее
. Если же условие не выполняется, то вновь удвоить число разбиений отрезка и сравнить два последних приближения так, как это было предложено выше. Закончить процесс при выполнении указанного условия и последнее  принять за искомое значение интеграла.
принять за искомое значение интеграла.
Этим приемом часто пользуются на практике, если трудно бывает оценить главный член погрешности.
6.1.4. Пример 1
Вычислим по методу левых прямоугольников интеграл  с точностью
с точностью 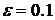 .
.
Разобьем отрезок 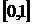 на 10 частей. Следовательно
на 10 частей. Следовательно  . Воспользуемся формулой:
. Воспользуемся формулой:
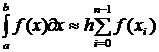 .
.
Тогда 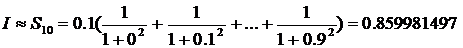
Теперь проделаем аналогичные расчеты для 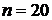 . Получим
. Получим 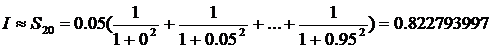
И сравним модуль разности полученных результатов с заданной точность:  . Принимаем за значение интеграла последнее полученное значение, т.е.
. Принимаем за значение интеграла последнее полученное значение, т.е.  .
.
6.1.5. Пример 2
Вычислим по методу трапеций интеграл  с точностью
с точностью 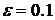
Разобьем отрезок 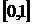 на 10 частей:
на 10 частей:  . Воспользуемся формулой:
. Воспользуемся формулой:
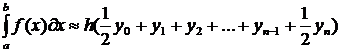 .
.
Тогда
 Теперь проделаем аналогичные расчеты для
Теперь проделаем аналогичные расчеты для 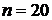 . Получим
. Получим
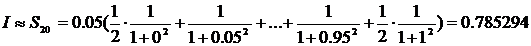
И сравним модуль разности полученных результатов с заданной точность:  . Принимаем за значение интеграла последнее полученное значение, т.е.
. Принимаем за значение интеграла последнее полученное значение, т.е. 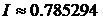 .
.
6.1.6. Пример 3
Вычислить по методу Симпсона интеграл  с точностью
с точностью 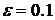 . Разобьем отрезок
. Разобьем отрезок 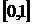 на 10 частей:
на 10 частей:  . Воспользуемся формулой:
. Воспользуемся формулой:
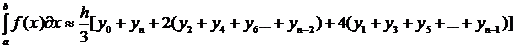
Тогда
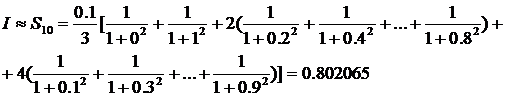
Теперь проделаем аналогичные расчеты для 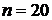 . Получим
. Получим
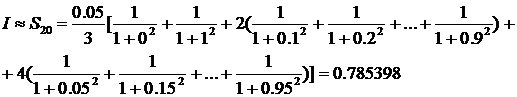
И сравним модуль разности полученных результатов с заданной точность: 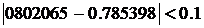 . Принимаем за значение интеграла последнее полученное значение, т.е.
. Принимаем за значение интеграла последнее полученное значение, т.е.  .
.
6.2. Лабораторная работа №9



 на участке нефтепровода.
на участке нефтепровода.

 и кремнефтористоводородной
и кремнефтористоводородной 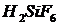 , благодаря растворению терригенных коллекторов, углубляет и развивает сеть каналов. Но одновременно и ограничивает приток пластовых вод к скважине за счет закупорки фильтрационных каналов в водоносном пласте осадками кремнефторидов.
, благодаря растворению терригенных коллекторов, углубляет и развивает сеть каналов. Но одновременно и ограничивает приток пластовых вод к скважине за счет закупорки фильтрационных каналов в водоносном пласте осадками кремнефторидов.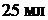 пластовой воды при температуре
пластовой воды при температуре  с кремнефтористоводородной кислотой
с кремнефтористоводородной кислотой 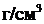

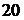 грамм песка и при объеме кислотного раствора
грамм песка и при объеме кислотного раствора 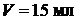 .
. , но аналитически посчитать его значение не представляется возможным из-за сложного вида подынтегральной функции. Известно, что значение определенного интеграла равно
, но аналитически посчитать его значение не представляется возможным из-за сложного вида подынтегральной функции. Известно, что значение определенного интеграла равно 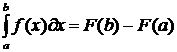 , где
, где 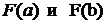 – значения первообразной
– значения первообразной 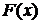 для подынтегральной функции
для подынтегральной функции 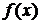 в точках
в точках 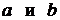 соответственно. Например,
соответственно. Например, 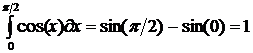 . Но далеко не для всякой функции
. Но далеко не для всякой функции 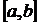 задана функция
задана функция 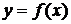 . С помощью точек
. С помощью точек 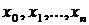 разобьем отрезок
разобьем отрезок  отрезков
отрезков 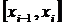 (
(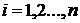 ), причем
), причем  . На каждом из этих отрезков выберем произвольную точку
. На каждом из этих отрезков выберем произвольную точку  и найдем произведение значения функции в этой точке
и найдем произведение значения функции в этой точке 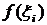 на длину отрезка
на длину отрезка 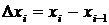 :
: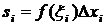 .
.
 называется интегральной суммой. Определенным интегралом от функции
называется интегральной суммой. Определенным интегралом от функции 
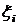 .
.
 0 проиллюстрирован на рисунке 1. Величины
0 проиллюстрирован на рисунке 1. Величины  , являющуюся длиной отрезка разбиения, называют шагом разбиения. В качестве
, являющуюся длиной отрезка разбиения, называют шагом разбиения. В качестве  ) или правые (
) или правые ( ) границы отрезков разбиения или их середины (
) границы отрезков разбиения или их середины (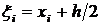 ). Получают следующие формулы метода прямоугольников, отвечающие этим трем способам выбора точек
). Получают следующие формулы метода прямоугольников, отвечающие этим трем способам выбора точек 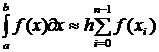
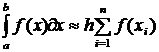
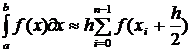
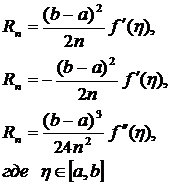
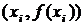 . В этом случае площадь под кривой на каждом отрезке разбиения заменяется площадью под прямой, которая равна площади прямоугольной трапеции с высотой
. В этом случае площадь под кривой на каждом отрезке разбиения заменяется площадью под прямой, которая равна площади прямоугольной трапеции с высотой 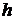 и основаниями
и основаниями  , т.е.
, т.е. 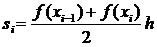 . Получается формула трапеций
. Получается формула трапеций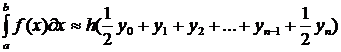 ,
,
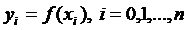 .
.
 .
.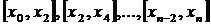 подынтегральная функция заменяется интерполяционным многочленом второй степени:
подынтегральная функция заменяется интерполяционным многочленом второй степени: 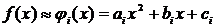

 можно принять интерполяционный многочлен Лагранжа второй степени, график которого проходит через точки
можно принять интерполяционный многочлен Лагранжа второй степени, график которого проходит через точки  , где
, где 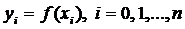 .
.
 ее первообразной будет
ее первообразной будет  .
.
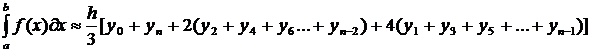 Главный член погрешности этой формулы равен:
Главный член погрешности этой формулы равен: .
. с заданной точность
с заданной точность 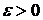 , т.е. получить такое приближенное значение его
, т.е. получить такое приближенное значение его 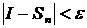 .
. , либо воспользовавшись следующим приемом.
, либо воспользовавшись следующим приемом.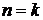 . Затем сделать такие же расчеты для
. Затем сделать такие же расчеты для  . Затем сравнить полученные результаты. Если окажется, что
. Затем сравнить полученные результаты. Если окажется, что 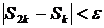 , то считать точность достигнутой и принять
, то считать точность достигнутой и принять  . Если же условие не выполняется, то вновь удвоить число разбиений отрезка и сравнить два последних приближения так, как это было предложено выше. Закончить процесс при выполнении указанного условия и последнее
. Если же условие не выполняется, то вновь удвоить число разбиений отрезка и сравнить два последних приближения так, как это было предложено выше. Закончить процесс при выполнении указанного условия и последнее  с точностью
с точностью 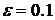 .
.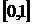 на 10 частей. Следовательно
на 10 частей. Следовательно  . Воспользуемся формулой:
. Воспользуемся формулой: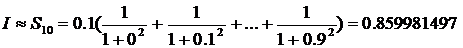
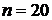 . Получим
. Получим 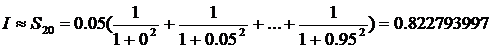
 . Принимаем за значение интеграла последнее полученное значение, т.е.
. Принимаем за значение интеграла последнее полученное значение, т.е.  .
.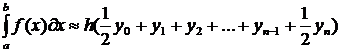 .
. Теперь проделаем аналогичные расчеты для
Теперь проделаем аналогичные расчеты для 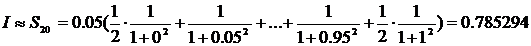
 . Принимаем за значение интеграла последнее полученное значение, т.е.
. Принимаем за значение интеграла последнее полученное значение, т.е. 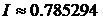 .
.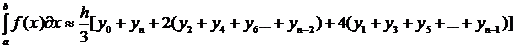
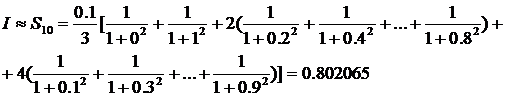
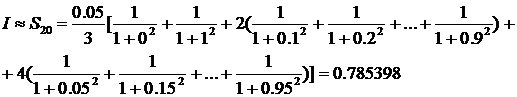
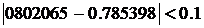 . Принимаем за значение интеграла последнее полученное значение, т.е.
. Принимаем за значение интеграла последнее полученное значение, т.е.  .
.


