Рассмотрим такую последовательность чисел:
1 2 4 8 16 32 64 128 …
Если присмотреться внимательно, то видно, что каждое последующее число от предыдущего отличается на одно и то же число, в нашем случае на «2». Вот это число, на которое отличается каждое последующее число от предыдущего, называют знаменателем и обозначают как q.
В общем случае запишем числовую последовательность так:
b1 b2 b3 … bn
Если 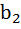 отличается от
отличается от 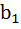 на q, то
на q, то 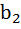 можно записать как
можно записать как 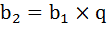 .
.
Тогда 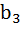 можно представить как
можно представить как 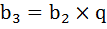 , но так, как нам известно, уже
, но так, как нам известно, уже
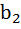 , подставим вместо него и получим
, подставим вместо него и получим  .
.
И так можно представить каждое последующее число вплоть до  , формула которого будет выглядеть так
, формула которого будет выглядеть так  .
.
Тогда эту последовательность:
b1 b2 b3 … bn
Можно представить таким образом:
b1 b1q b1q2 … b1qn-1
Нас будет интересовать сумма всех слагаемых этой последовательности чисел, чему она будет равна. Давайте, выведем сумму геометрической последовательности чисел. Обозначим сумму как S.
Тогда сумма S такой последовательности будет выглядеть так:
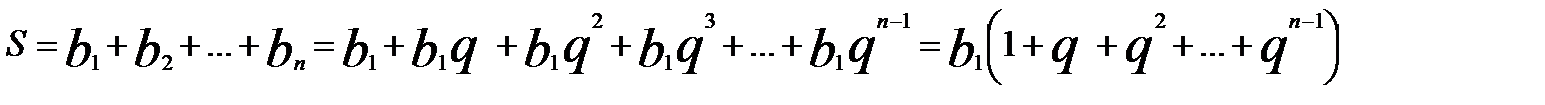
Давайте эту скобку  обозначим любой буквой, например, K.
обозначим любой буквой, например, K.
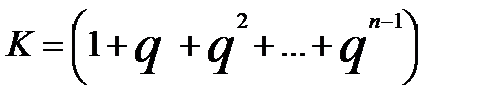
Для того, чтобы избавиться от  умножим и левую часть и правую на q, ведь от этого ничего не изменится, но за то мы получим следующее выражение:
умножим и левую часть и правую на q, ведь от этого ничего не изменится, но за то мы получим следующее выражение:
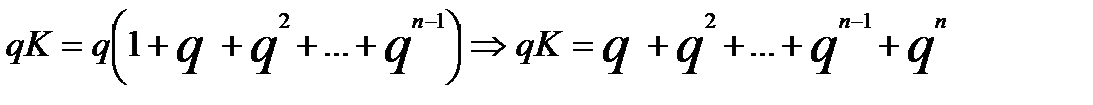
Теперь, если мы в правой стороне равенства одновременно прибавим единицу и отнимем единицу, у нас тоже ничего не изменится, но за то мы получим следующее выражение:

Ну а так как 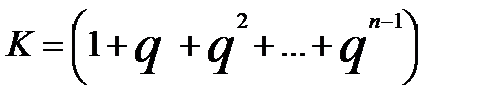 , то получаем следующее выражение:
, то получаем следующее выражение:
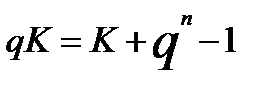
Всё, что относится к K, мы выразим слева, остальное справа:

Тогда в этой, в основной формуле:
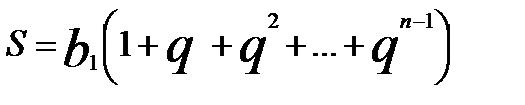
Мы получили, что 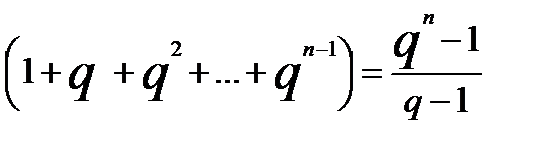 .
.
Заменим и получим формулу суммы геометрической прогрессии:
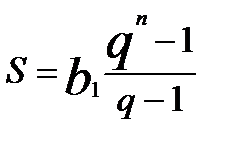
Вот таким нехитрым способом мы выявили главную формулу грабежа всех времён и народов J
Ренты.
Геометрическая прогрессия является корневым понятием для расчётов всех кредитов, облигаций, для прогнозирования денежных потоков бизнеса, и вообще для понимания любых финансовых расчётов.
Есть шесть функций денег, выведем и поймём формулы двух функций и на их основе выведем остальные. Эти функции чрезвычайно важны для понимания сути механизма работы многих финансовых инструментов.
Для начала разберёмся с обозначениями. Те деньги, которые есть у нас здесь и сейчас на руках обозначим, как PV. Те же деньги, которые у нас будут в будущем, либо при помощи периодического накопления, либо единичного вложения в некий финансовый инструмент обозначим как FV.
Периодические платежи, которые, либо к нам поступают в карман, либо наоборот уходят с нашего кармана, стабильно один раз в некоторый одинаковый по времени отрезок, мы будем называть аннуитетом и обозначать, либо a, либо PMT, что одно и то же.
Процентную ставку будем рассматривать в десятичной дроби и обозначать, как i. Срок жизни финансового инструмента, который генерирует, либо приток в наш карман, либо отток с нашего кармана будем обозначать n.
У нас есть всего два денежных потока, которые могут генерировать абсолютно все финансовые инструменты, либо отрицательный для нас денежный поток, то есть когда деньги будут уходить с нашего кармана, либо положительный, когда некий финансовый инструмент будет класть деньги в наш карман. Все потоки связаны между собой. Давайте визуализировать их и глубоко понимать.
Первая функция, которую мы рассмотрим - будущую стоимость денежной единицы.
Что это такое? Будем для примера и понимания рассматривать пока два примитивных финансовых инструмента – это депозит и кредит. Но нужно понимать, что любой сложный финансовый инструмент на самом деле состоит из этих двух примитивных схем.
Представим, что у нас есть некая сумма PV на руках прямо здесь и сейчас, мы хотим положить её на депозит под некую процентную ставку, не забываем, что мы сразу её превращаем в дробь, i на n лет. Также нужно понимать, что каждый год нам будут начисляться проценты, то есть некая прибавка к сумме PV, а также проценты, начиная со второго года, будут начисляться и на накопленные проценты, нарастая как снежный ком J Вот поэтому таких депозитов и не существует, максимум на год есть депозиты! Ну а теперь, давайте выразим это алгебраически:
первый год 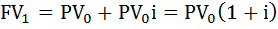
второй год 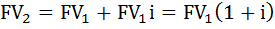 , а так как
, а так как  мы уже вычислили, заменим её и получим
мы уже вычислили, заменим её и получим 
…
n-й год, мы уже видим зависимость и сразу можем выразить 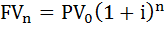
Вот так выглядит окончательная формула 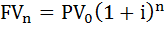 , она показывает, сколько денег у нас накопится на депозите, если мы прямо сейчас положим на депозит
, она показывает, сколько денег у нас накопится на депозите, если мы прямо сейчас положим на депозит  денег под i процентов годовых на n лет.
денег под i процентов годовых на n лет.
Если представить  , то первая функция денег означает накопление денег от единичного, то есть одноразового вклада денег, допустим на депозит, и как будет выглядеть первоначальное вложение, то есть в какую сумму превратиться оно и выглядит эта формула так:
, то первая функция денег означает накопление денег от единичного, то есть одноразового вклада денег, допустим на депозит, и как будет выглядеть первоначальное вложение, то есть в какую сумму превратиться оно и выглядит эта формула так:
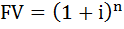
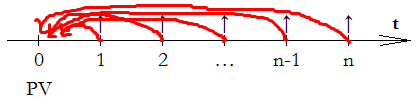
Вторая функция денег. Аннуитет постнумерандо будущей стоимости с ежегодным начислением процентов. Аннуитет – это когда мы каждый равный период времени, в нашем случае каждый год, кладём на депозит одну и ту же сумму a. Постнумерандно – это в конце каждого периода, если в условии сказано в начале каждого периода, то говорят пренумерандно. И в итоге, мы должны рассчитать накопленную сумму, вместе с процентами FV.
На рисунке чётко видно схему движения денег, можно визуально представить. Стрелочки вниз – это денежные потоки, то есть наши равные вложения в каждый равный промежуток времени на депозит. Представим это алгебраически:
FV = a(1+i)n-1 + a(1+i)n-2 + … + a

Вложение a денег в конце первого года, мы должны нарастить до n лет, обозначим красным цветом на картинке выше. А синим цветом обозначим, тот период, который не участвует в наращивании денег. Выходит первое вложение денег a наращивается n -1 лет, это, если посмотреть внимательней, первая функция денег. И по такой логике мы будем наращивать и второе вложение денег, сумма, которой тоже a, так как у нас аннуитет, смотрите картинку ниже:
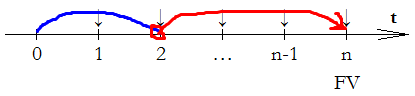
И так далее, вплоть до периода n, когда сумма a не будет уже наращиваться.
Теперь, давайте, вынесем за скобку a:
a(1+(1+i)+…+(1+i)n-1)
Мы видим похожую ситуацию, которую мы видели при выведении формулы геометрической прогрессии:
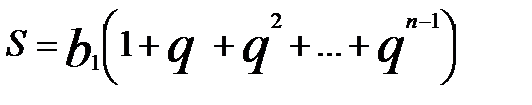
Похоже? Тогда 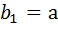 ,
, 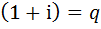 . А так как:
. А так как:
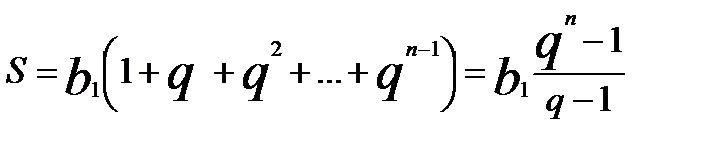
Подставим вместо 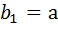 ,
, 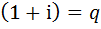 , и получим:
, и получим:

Пусть a =1$, тогда формула накопления единицы, или будущая стоимость аннуитета за период n будет выглядеть так:
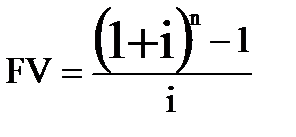
Рассмотрим третью функцию денег. Сначала мы положили один доллар на n лет под i процентов годовых и вывели формулу будущего стоимости одного доллара 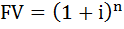 . Затем, мы каждый год откладывали в течении n лет по одному доллару на депозит под i процентов годовых, и получили будущую стоимость аннуитета
. Затем, мы каждый год откладывали в течении n лет по одному доллару на депозит под i процентов годовых, и получили будущую стоимость аннуитета 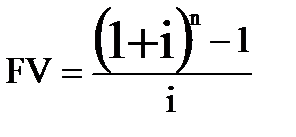 .
.
Теперь, смоделируем такую ситуацию. Мы хотим накопить некую сумму FV денег на депозите, через n лет и зная i. Сколько же нужно каждый год вкладывать на депозит PMT? Воспользуемся известной нам формулой.
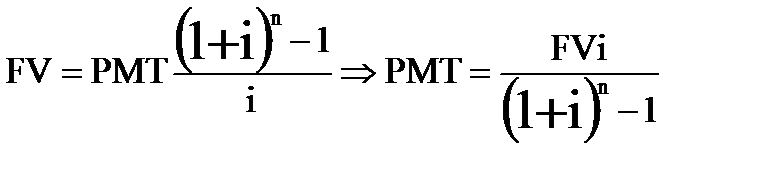
Теперь, представим, что мы хотим накопить один доллар США, то есть FV=1$, тогда 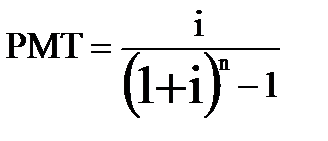 .
.
Таким образом, мы вывели третью функцию денег, которая является ключевой и важной функцией! Она применяется во многих финансовых инструментах, и которая называется - фактор фонда возмещения! Ещё её называют денежный поток!
Итак, мы рассмотрели три функции денег. Все они были связаны с будущей стоимостью денег через n лет.
Теперь рассмотрим оставшиеся три функции, как наверно, не трудно догадаться, они будут теперь связаны с текущей стоимостью денег, то есть здесь и сейчас, а не как в прошлых функциях, через n лет.
Четвёртая функция тесно связана с первой функцией. Если в первой функции, давайте вспоминать, нам была известна текущая стоимость денег, и надо было найти будущую стоимость 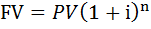 , этот процесс называется наращивание или компаудинг. То обратный процесс, когда нам известна будущая стоимость, ну например, мы хотим накопить 1 долл через n лет, сколько нужно вложить сейчас под i процентов годовых? Этот процесс уже называется дисконтирование. С этой формулы, легко вывести неизвестное нам PV:
, этот процесс называется наращивание или компаудинг. То обратный процесс, когда нам известна будущая стоимость, ну например, мы хотим накопить 1 долл через n лет, сколько нужно вложить сейчас под i процентов годовых? Этот процесс уже называется дисконтирование. С этой формулы, легко вывести неизвестное нам PV:

Теперь представим, что FV=1$, тогда окончательно функция текущей стоимости единицы будет равно:

Таким же образом и с такой же логикой выведем пятую функцию денег, так называемую текущую стоимость аннуитета:
На картинке выше, представим, что нам известна сумма, равновеликая, которую мы можем в одинаковый отрезок времени, в нашем случае раз в год, оплачивать, ну допустим по кредиту. Какую сумму мы можем тогда взять в кредит здесь и сейчас? Вот на этот вопрос и отвечает функция текущей стоимости аннуитета. Это в чистом виде дисконтирование будущих денежных потоков.
Давайте, аккуратно выведем формулу. Продисконтируем каждый денежный поток:
первый год 
второй год 
…
n-й год 
Теперь найдём сумму текущих стоимостей денежного потока:
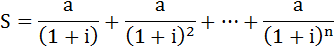
Вынесем за скобку a.
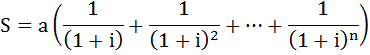
Для упрощения давайте дробь обозначим как 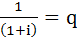 .
.
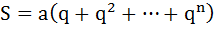
Давайте теперь рассмотрим эту скобку  отдельно, чтобы не запутаться. Теперь, давайте, прибавим единичку и сразу же отнимем, в общем, ничего не поменяется, но за то мы получим следующее выражение:
отдельно, чтобы не запутаться. Теперь, давайте, прибавим единичку и сразу же отнимем, в общем, ничего не поменяется, но за то мы получим следующее выражение:

Мы помним, что  , тогда общая формула будет выглядеть так
, тогда общая формула будет выглядеть так 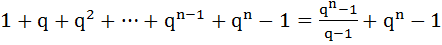 .
.
Вернём обратно в этой формуле 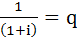 , тогда:
, тогда:
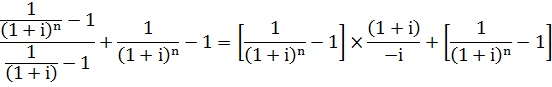
Вынесем за скобку 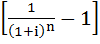 и получим:
и получим:

Вынесем знак вперёд, и тогда получится:
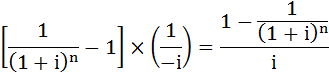
Тогда
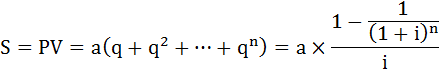
Представим теперь, что мы хотим выплачивать один доллар, то есть a=1$, тогда окончательная формула текущей стоимости аннуитета будет выглядеть так:
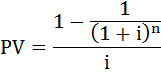
И, выведем шестую функцию.
Суть этой функции такая, мы здесь и сейчас взяли кредит и теперь нам надо посчитать платёж, который нужно делать в одинаковый период времени в течении n лет, чтобы вернуть и первоначальный кредит и проценты по кредиту.

Представим, что мы взяли в кредит 1 долл., тогда взнос на амортизацию единицы будет выглядеть так: 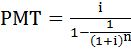 .
.
Все формулы функций, которые мы вывели собраны все в одной таблице ниже. Конечно же запоминать их наизусть не стоит, сейчас можно всё автоматизировать, но суть надо конечно же понимать и хотя бы один раз вывести все формулы.
Во всех формулах выше мы рассматривали денежные потоки с ежегодным начислением процентов. Но чаще всего начисления процентов бывают ежемесячные, квартальные и полугодовые. Для расчёта таких начислений нужно i делить на рассматриваемый период, а n умножать на этот самый период.
Мы с вами уже знаем, и понимаем, как получилось, число «пи»- π. Но есть ещё одно число, которое очень часто встречается в финансах и в инженерии. Это число «е»- e, оно примерно равно e=2.7183. Это число пришло с банковских расчётов.

Эта первая функция денег – будущая стоимость единицы. В этой формуле показано начисление процентов m раз в год. Оказывается, если начислять проценты чаще, то доход будет выше. Для примера, давайте возьмём 1 доллар и положим мысленно на депозит на один год под 100% годовых. На рисунке ниже, видны результаты начисления процента, в каждой таблице увеличивая частоту начисления процентов от одного раза в год до ежесекундного начисления:

Но оказывается, увеличивая частоту начислений, сумма не устремляется к бесконечности, а стремится, оказывается к конкретному числу, но стремится оно к нему бесконечно. Сначала разница существенная, но с каждым разом увеличивая частоту начислений, постепенно эта разница стремится к нулю, а сама сумма к некому числу e. На картинке ниже и на графике это отчётливо видно:
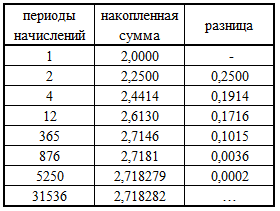

То есть, часто в финансах и инженерии, принимают непрерывное начисление процентов, и вот так оно выглядит:

Вектора
Главная цель математики, физики, как ни странно – это не решение задач, как нас учили в школе, главная цель математики и физики, носит чисто прикладной характер и зарываться, глубоко не стоит. Важно просто понять, как устроен мир, это понимание должно приходить с разных углов, в том числе и с инженерной точки зрения и понимания!
Большинство физических явлений, таких как скорость, сила, вес, ускорение и т.п. имеют не просто свою размерность, но и самую важную характеристику – направление! Возьмём силу, сила выражается в Ньютонах, но что ещё важнее как направлена сила, понимание направленности силы нам даёт возможность, например, укрепить дом от внешних сил (ветер, снеговая нагрузка, землетрясение, ураганы). Понимая направление силы, мы можем, видя деформацию какого-либо материала, с высокой точностью вероятности сказать причину этой деформации.
Во всём этом нам помогает понимание векторов! Вектор – это всего лишь на всего направленный отрезок! Он как раз таки показывает направление физического явления! Давайте, научимся оперировать векторами, ничего сложного здесь нет.
Для облегчения понимания многих явлений люди придумали систему координат, чтобы визуализировать многие процессы. Вектор – это отрезок на этой координате, нарисованный в виде линии со стрелкой, стрелка показывает, куда направляется некое физическое явление, для простоты и понимания, давайте далее рассматривать пример с расстоянием или ещё его называют путь!
Вектор, помимо направления имеет и размерность, которую называют скалярной величиной вектора, например, путь, имеет размерность в метрах, то есть характеризуется неким числом.
Приведём несколько понятий. Вектор обычно обозначается маленькой латинской буквой, с верхней чёрточкой над буквой - 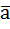 . Либо заглавными латинскими буквами, где первая буква показывает начало отрезка, а вторая буква конец отрезка -
. Либо заглавными латинскими буквами, где первая буква показывает начало отрезка, а вторая буква конец отрезка -  .
.
Точка – это тоже вектор, где начало и конец совпадают. Когда два или более вектора параллельны друг другу, то их называют коллинеарными, а если они ещё и направлены в одну и ту же сторону, то и сонаправленными ещё.
Рассмотрим сложение двух векторов. Допустим, у нас есть два вектора: 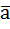 и
и 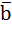 . Чтобы их сложить нужно, как бы соединить их, то есть к концу одного вектора
. Чтобы их сложить нужно, как бы соединить их, то есть к концу одного вектора 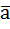 приложить вектор
приложить вектор 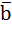 . Чтобы представить это визуально, давайте представим, что мы идём по тротуару. Сначала мы шли с точки A вверх и вправо, затем свернули вниз и дошли до точки C. Мы пришли к цели, пройдя n метров пути, это есть скалярная величина, но в итоге мы же переместились с начальной точки A до точки C, это и есть вектор нашего перемещения!
. Чтобы представить это визуально, давайте представим, что мы идём по тротуару. Сначала мы шли с точки A вверх и вправо, затем свернули вниз и дошли до точки C. Мы пришли к цели, пройдя n метров пути, это есть скалярная величина, но в итоге мы же переместились с начальной точки A до точки C, это и есть вектор нашего перемещения!
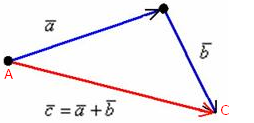 Сначала вектор нашего перемещения был вектор
Сначала вектор нашего перемещения был вектор 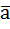 , затем вектор
, затем вектор 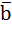 , но в итоге выйдя с точки A, мы оказались в точке C, то есть, по сути, мы прошли вектор
, но в итоге выйдя с точки A, мы оказались в точке C, то есть, по сути, мы прошли вектор  , только окольными путями. Вот этот вектор
, только окольными путями. Вот этот вектор  и есть сложение двух векторов:
и есть сложение двух векторов: 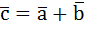 . Думаю, это логично!
. Думаю, это логично!
Вот тут будьте предельно внимательными, здесь заложена простая, но очень действенная логика. Я специально внизу на картинках сделал разметку одинаковыми по размеру квадратиками.
Два вектора, отложенные от начала координат и расположенных ортогонально (перпендикулярно) друг к другу, имеющих одинаковый размер равной единице, то есть длине квадратика, называют единичными векторами 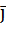 и
и  или ортами:
или ортами:
Тут логика такая, и пора уже нам понять, что всё в мире взаимосвязано и фрактально, так мы до этого складывали вектора, теперь мы любой вектор можем разложить на единичные вектора, что удобно визуализировать.
На картинке ниже вектор 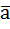 мы разложим на единичные вектора таким образом: по оси Y – это две клетки вверх, то есть два единичных вектора
мы разложим на единичные вектора таким образом: по оси Y – это две клетки вверх, то есть два единичных вектора 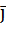 . По оси X – это три клетки вправо, то есть три единичных вектора
. По оси X – это три клетки вправо, то есть три единичных вектора  .
.
Получается: 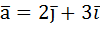 . Это и удобно визуализировать и логично и имеет глубокий смысл:
. Это и удобно визуализировать и логично и имеет глубокий смысл:
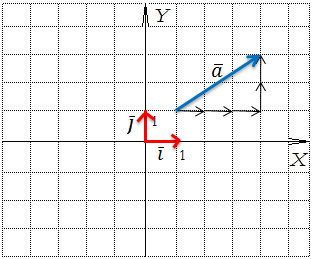
По оси X, если вектор направлен вправо, то считается, что вектор направлен со знаком плюс, если влево, то со знаком минус. По оси Y, если вектор направлен вверх, то знак плюс, если вниз – знак минус.
Давайте закрепим навык, несколько векторов разложим на единичные вектора.
Представим силу, которая направлена так, как на картинке снизу, оказывается, эта сила состоит из двух сил (в разделе физика будут подробности): 
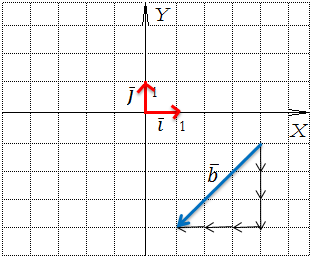
Представляем дальше. На картинке снизу представим две силы, разложим их: 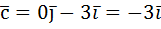 ;
; 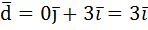 .
.
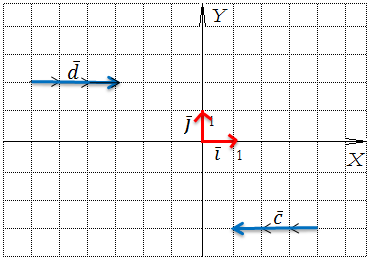
Думаю, это было не сложно и легко мы это всё представили.
Теперь, давайте научимся выполнять операции над векторами: сложение и вычитание векторов, умножение на число.
Сложение двух векторов мы уже выполнили, единственно добавлю логику сложения. Если два вектора сонаправлены, то есть стрелки направлены в одну и ту же сторону (положительную или отрицательную), то их мы соединяем от начала двух векторов, как на картинке ниже:
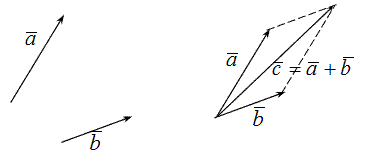
И суммой сонаправленных векторов будет диагональ параллелограмма. То есть сначала рисуем или правильнее сказать дорисовываем мысленно параллелограмм, а потом уже диагональ, которая и будет являться вектором сложения двух векторов!
Если же два вектора направлены в разные стороны, то есть один вектор положительно, а другой отрицательно, то их соединять нужно к концу вектора, то есть к стрелке, как на картинке ниже:
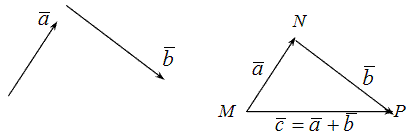
При таком сложении действует уже правило треугольника, то есть рисуем треугольник.
Разность векторов 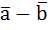 находится от обратного, нужно построить такой вектор, что
находится от обратного, нужно построить такой вектор, что  :
:

Вектор, умножая на некое число α, длина отрезка просто увеличится в α раз. На картинке ниже вектора 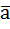 умножаем на разные числа:
умножаем на разные числа:
Разберёмся теперь с координатами векторов!
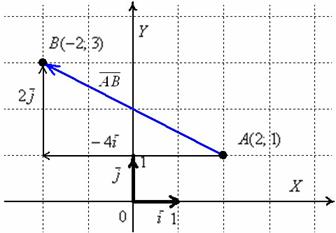 У вектора
У вектора  есть две точки, отрезок, соединяющий эти две точки и направление, куда направлена стрелка. У точек в координатной плоскости есть свой адрес, положение по оси X и положение по оси Y. В нашем примере, на картинке слева, точка A имеет координаты A(2;1), а точка B соответственно B(-2;3). Зная эти координаты точек, мы легко можем разложить вектор по базису, а разложение вектора по базису – это и есть координаты самого вектора (не путать с координатами точек A и B). Для того чтобы разложить вектор по базису, зная координаты точек, нужно просто узнать размер отрезка вектора
есть две точки, отрезок, соединяющий эти две точки и направление, куда направлена стрелка. У точек в координатной плоскости есть свой адрес, положение по оси X и положение по оси Y. В нашем примере, на картинке слева, точка A имеет координаты A(2;1), а точка B соответственно B(-2;3). Зная эти координаты точек, мы легко можем разложить вектор по базису, а разложение вектора по базису – это и есть координаты самого вектора (не путать с координатами точек A и B). Для того чтобы разложить вектор по базису, зная координаты точек, нужно просто узнать размер отрезка вектора  по оси X и размер отрезка вектора
по оси X и размер отрезка вектора  по оси Y. А отрезок можно узнать так: координаты точки B вычесть координаты точки A по оси X. Также и по оси Y.
по оси Y. А отрезок можно узнать так: координаты точки B вычесть координаты точки A по оси X. Также и по оси Y. 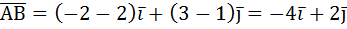 - это и есть координаты самого вектора!
- это и есть координаты самого вектора!
Научимся теперь измерять длину самого вектора. Если вектор разложить по базису, то применив теорему Пифагора, то мы легко вычислим размер отрезка вектора  , при этом мы пренебрежём знаком, так как нас интересует абсолютное значение, для этого возьмём модуль вектора, и формула будет следующей:
, при этом мы пренебрежём знаком, так как нас интересует абсолютное значение, для этого возьмём модуль вектора, и формула будет следующей:
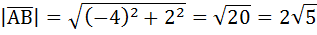
Это и есть размер вектора 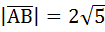 .
.
Теперь научимся складывать вектора через координаты.
Помним, что координаты вектора – это разложение вектора по базису. Давайте сразу на примере представим сложение, вычитание векторов и умножение числа на вектор. Допустим, у нас есть два вектора и его координаты 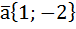 и
и  , давайте сложим эти два вектора через координаты, вычтем вектор
, давайте сложим эти два вектора через координаты, вычтем вектор 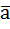 от вектора
от вектора 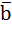 и умножим вектор
и умножим вектор 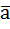 на 2.
на 2.
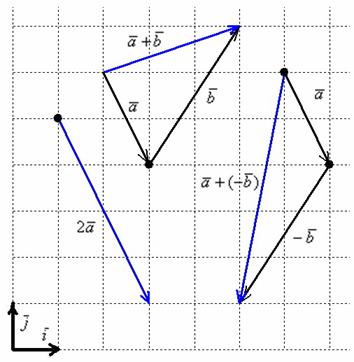
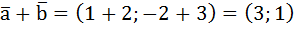 то есть при сложении векторов их координаты складываются, думаю это логично и понятно особенно это чётко видно на изображении слева.
то есть при сложении векторов их координаты складываются, думаю это логично и понятно особенно это чётко видно на изображении слева.
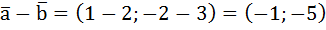 при вычитании координаты вычитаются. При умножении все координаты умножаются на число.
при вычитании координаты вычитаются. При умножении все координаты умножаются на число.
 Теперь, давайте, познаем и выведем формулу скалярного произведения векторов. Допустим, у нас есть два вектора
Теперь, давайте, познаем и выведем формулу скалярного произведения векторов. Допустим, у нас есть два вектора 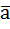 и
и 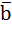 , с координатами
, с координатами 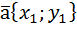 и
и  .
.
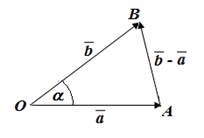
Вектор 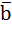 расположен под углом α к вектору
расположен под углом α к вектору 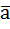 . Найдём скалярное произведение векторов, выведем формулу. Итак, вектор
. Найдём скалярное произведение векторов, выведем формулу. Итак, вектор  . У нас есть треугольник OAB, по теореме косинусов, зная длину двух отрезков и угол между ними, можно легко посчитать противоположную углу сторону.
. У нас есть треугольник OAB, по теореме косинусов, зная длину двух отрезков и угол между ними, можно легко посчитать противоположную углу сторону.
Для начала, вот выше картинка, алгебраические свойства вычисления модулей. Они нам пригодятся для дальнейших вычислений.
Значит, вычислим по теореме косинусов отрезок, то есть длину вектора 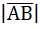 :
:

С другой стороны у нас  , и если мы возьмём квадрат, то используя бином Ньютона и алгебраические свойства модулей, получим:
, и если мы возьмём квадрат, то используя бином Ньютона и алгебраические свойства модулей, получим:

Перепишем эту формулу по-другому:
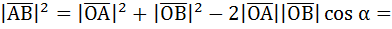
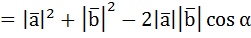
Так как 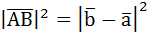 , то получим:
, то получим:
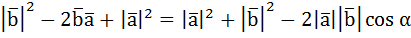
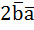 отправим в правую сторону равенства, а всё что справа от знака равно на левую часть, тогда получим:
отправим в правую сторону равенства, а всё что справа от знака равно на левую часть, тогда получим:

После сокращения у нас осталось: 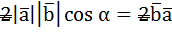 , после сокращения получилось скалярное произведение векторов:
, после сокращения получилось скалярное произведение векторов:

Теперь выведем формулу скалярного умножения через координаты.
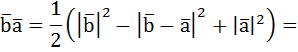
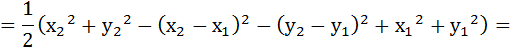
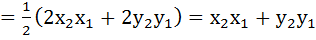 .
.
Результатом скалярного произведения векторов является число.
Векторное же произведение векторов рассчитывается как площадь параллелограмма, а результатом является вектор, который направлен ортогонально двум векторам по правилу правого буравчика.
Как найти площадь параллелограмма, зная только две стороны и угол между ними, давайте выведем формулу.
 Если параллелограмм поделить с помощью диагонали на две части, у нас получится два одинаковых треугольника. Найдём площадь одного треугольника и умножим на два.
Если параллелограмм поделить с помощью диагонали на две части, у нас получится два одинаковых треугольника. Найдём площадь одного треугольника и умножим на два.
Чтобы воспользоваться углом, как обычно поделим треугольник на два прямоугольных треугольника. Абстрагируемся пока от векторов, примем этот треугольник за обычный треугольник. Тогда сторона 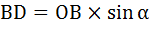 , а сторона
, а сторона 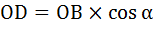 . Тогда площадь треугольника ODB:
. Тогда площадь треугольника ODB:
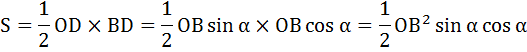
Теперь площадь треугольника DAB посчитаем:


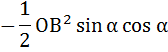
Теперь, давайте просуммируем площади двух треугольников:
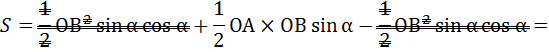
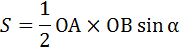
Тогда площадь параллелограмма будет равна:
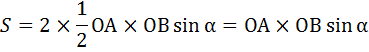
Отсюда векторное произведение двух векторов будет равно:
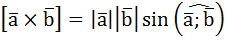 .
.
Теория чисел
 Как и во всём, в теории чисел действует принцип «матрёшки». И эта матрёшка уходит вглубь до бесконечности, повторяя собой модель бесконечной вселенной. А мы своим трёхмерным умом, иногда четырёхмерным, можем пока видеть несколько порядков чисел, и соотвественно с этим видением строить технологии, станки, машины, дома, бизнесы, выстраивать и конструировать ценные бумаги и т.п.
Как и во всём, в теории чисел действует принцип «матрёшки». И эта матрёшка уходит вглубь до бесконечности, повторяя собой модель бесконечной вселенной. А мы своим трёхмерным умом, иногда четырёхмерным, можем пока видеть несколько порядков чисел, и соотвественно с этим видением строить технологии, станки, машины, дома, бизнесы, выстраивать и конструировать ценные бумаги и т.п.
Число помогает выразить большинство физических явлений через некую размерность. Помогает визуализировать и понять много это или мало, прибыльно или убыточно, считать предельные нагрузки и т.д.
Начинаем мы как обычно с простых чисел, таких как: 1 2 3 … ∞. Такие числа называют натуральные числа и обозначают так 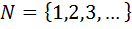 . Натуральные числа делятся на простые и составные числа в свою очередь. Натуральные числа всегда положительны.
. Натуральные числа делятся на простые и составные числа в свою очередь. Натуральные числа всегда положительны.
Следующее множество – это целые числа, сюда входит множество натуральных чисел плюс отрицательные числа, то есть противоположные по знаку натуральным числам, и обозначаются как: 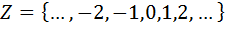 .
.
Очередное числовое семейство – это множество рациональных чисел, их обозначают: 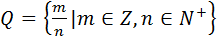 . По сути, говоря рациональное число – это дробь, и появилось оно, когда человеку понадобилось делить некое целое число (в виде объёма, площади, дохода и прочее) на несколько кусков или долей. Обычно результатом дроби является целое число, либо десятичное число, например:
. По сути, говоря рациональное число – это дробь, и появилось оно, когда человеку понадобилось делить некое целое число (в виде объёма, площади, дохода и прочее) на несколько кусков или долей. Обычно результатом дроби является целое число, либо десятичное число, например:  , либо периодическая десятичная дробь, к примеру, число
, либо периодическая десятичная дробь, к примеру, число  , здесь число три, после запятой повторяется бесконечно. Дроби бывают правильные и неправильные.
, здесь число три, после запятой повторяется бесконечно. Дроби бывают правильные и неправильные.
Рассмотрим, множество иррациональных чисел, обозначают их так: 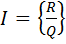 . Иррациональное число включает в себя множество всех выше, рассмотренных чисел, и все они вместе составляют множество вещественных или как ещё говорят множество действительных чисел R. Иррациональное число – можно представить в виде дроби, результатом которого является бесконечное непериодическое десятичное число, или извлечь корень. Из всех множеств, именно иррациональные числа являются самыми загадочными, например такие знаменитые числа:
. Иррациональное число включает в себя множество всех выше, рассмотренных чисел, и все они вместе составляют множество вещественных или как ещё говорят множество действительных чисел R. Иррациональное число – можно представить в виде дроби, результатом которого является бесконечное непериодическое десятичное число, или извлечь корень. Из всех множеств, именно иррациональные числа являются самыми загадочными, например такие знаменитые числа: 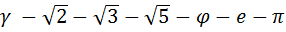 . Интересны они тем, что мы отобразить их на числовой прямой можем, лишь приближённо. Так как, только округлив, мы можем их отобразить, а так оно стремится к некому числу бесконечно, но никогда не достигнет его J
. Интересны они тем, что мы отобразить их на числовой прямой можем, лишь приближённо. Так как, только округлив, мы можем их отобразить, а так оно стремится к некому числу бесконечно, но никогда не достигнет его J
Все числа обычно рассматривают для лучшей визуализации на числовой прямой:
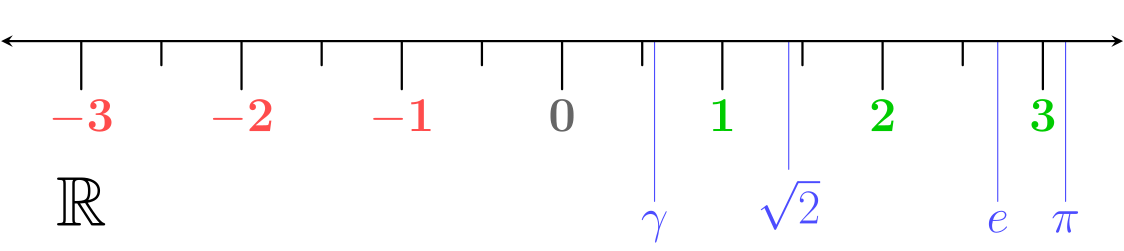
И, последнее множество, которое мы рассмотрим – это множество комплексных чисел, обозначаемых как C. Остановимся на них подробней.
На числовой прямой вещественных чисел, как оказалось не все решения уравнений можно отобразить, есть числа, которые, отображаются в виде точки, которая не пересекается с осями вещественных чисел, имеется разрыв. Они как бы возникают из ниоткуда, а точнее из какого-то другого измерения. И уравнение как, оказывается, имеет решение. Например, уравнение  , на оси вещественных чисел не имеет решение, но на самом деле решение есть, и оно приходит с другого измерения. Да-да, так оно и есть, только назвали это число мнимой единицей и обозначили как
, на оси вещественных чисел не имеет решение, но на самом деле решение есть, и оно приходит с другого измерения. Да-да, так оно и есть, только назвали это число мнимой единицей и обозначили как 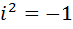 .
.
Для визуализации комплексных чисел придумали дополнительную ось мнимых единиц, расположили перпендикулярно оси вещественных чисел, так как они пересекаются и комплексное число выглядит так: 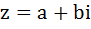 , где
, где 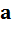 – это множество вещественных чисел, а
– это множество вещественных чисел, а 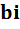 - множество мнимых единиц.
- множество мнимых единиц.
 А так как комплексное число возникает с другого измерения, то его отображают в виде вектора, при этом вещественную часть числа откладывают по горизонтальной оси вещественных чисел, а мнимую часть откладывают по вертикальной оси мнимых единиц, а сам вектор направлен с нуля на пересечение этих множеств.
А так как комплексное число возникает с другого измерения, то его отображают в виде вектора, при этом вещественную часть числа откладывают по горизонтальной оси вещественных чисел, а мнимую часть откладывают по вертикальной оси мнимых единиц, а сам вектор направлен с нуля на пересечение этих множеств.
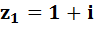 - на картинке слева чёрным цветом мы отобразили вектор этого числа, далее просто по цвету, вы найдёте вектор комплексного числа…
- на картинке слева чёрным цветом мы отобразили вектор этого числа, далее просто по цвету, вы найдёте вектор комплексного числа… 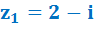 ;
;  ;
; 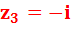 ;
; 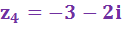 ;
; 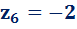 .
.
Думаю, понятно, что вещественное число мы откладывали по вещественной оси, а мнимую часть по мнимой оси, пересечение – это и есть само комплексное число!
Теперь, осталось научиться обращаться с комплексными числами, научимся делать, то, что умеем делать с вещественными числами, а именно складывать, вычитать, умножать, делить, возводить в степень и извлекать корень.
На примере будет нам проще. Итак, допустим у нас два комплексных числа: 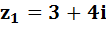 и
и 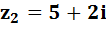 .
.
Сначала сложим эти два комплексных числа. При сложении вещественные части комплексного числа складываются отдельно, а мнимая часть отдельно:

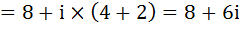
Теперь вычтем эти два комплексных числа:
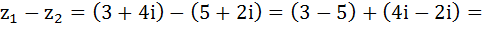
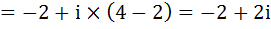
Теперь умножим эти же два комплексных числа:

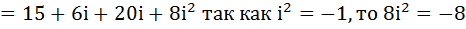
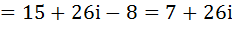
Теперь разделим эти два комплексных числа:
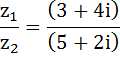
Для деления двух комплексных чисел, по логике нужно избавиться в знаменателе от мнимой единицы. Рассмотрим знаменатель отдельно. Для того, чтобы избавиться от мнимой единицы нужно комплексное число умножить на сопряжённое ей комплексное число, что значит умножить на такую же скобку, только с противоположным знаком:

Так как в знаменателе мы умножили на сопряжённое число, то и числитель надо умножить на это же число.
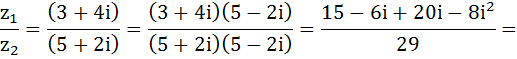
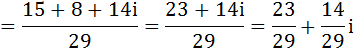
А теперь мы научимся выражать комплексные числа в тригонометрической форме, как это мы научились делать с вещественными числами.
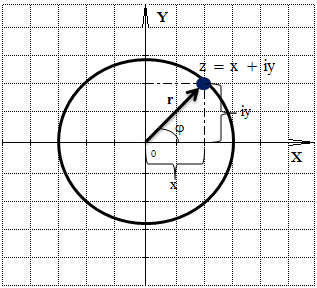
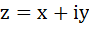 – отобразим это число на числовой оси. По оси X будем отображать вещественные числа, по оси Y мнимые единицы. Как мы уже знаем, что любое комплексное число представляет собой вектор, который разлагается на вещественную часть и мнимую, отобразим этот вектор r на картинке выше. Синяя жирная точка – это и есть комплескное число z. Вектор r одновременно можно представить и как радиус окружности с углом φ.
– отобразим это число на числовой оси. По оси X будем отображать вещественные числа, по оси Y мнимые единицы. Как мы уже знаем, что любое комплексное число представляет собой вектор, который разлагается на вещественную часть и мнимую, отобразим этот вектор r на картинке выше. Синяя жирная точка – это и есть комплескное число z. Вектор r одновременно можно представить и как радиус окружности с углом φ.
Тогда вещественное число x можно представить через косинус угла:
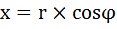 , а мнимую часть через синус угла:
, а мнимую часть через синус угла: 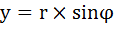 .
.
Теперь вместо такой записи комплексного числа 
|
|
|



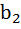 отличается от
отличается от 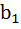 на q, то
на q, то 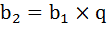 .
.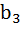 можно представить как
можно представить как 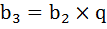 , но так, как нам известно, уже
, но так, как нам известно, уже  .
. , формула которого будет выглядеть так
, формула которого будет выглядеть так  .
.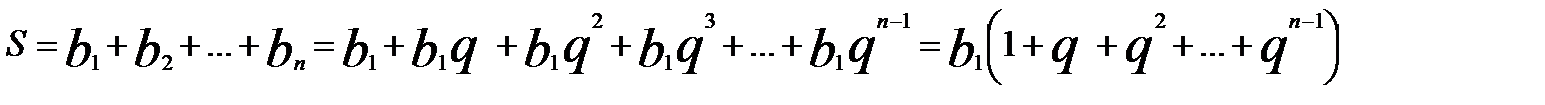
 обозначим любой буквой, например, K.
обозначим любой буквой, например, K.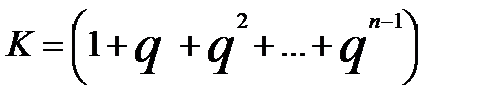
 умножим и левую часть и правую на q, ведь от этого ничего не изменится, но за то мы получим следующее выражение:
умножим и левую часть и правую на q, ведь от этого ничего не изменится, но за то мы получим следующее выражение: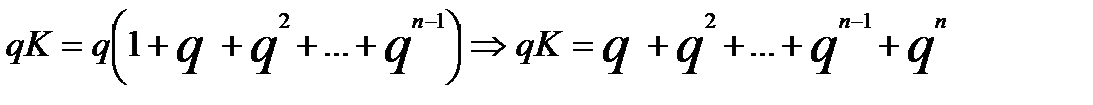

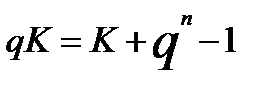

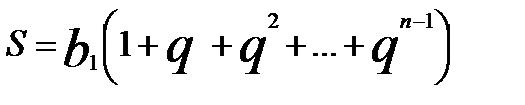
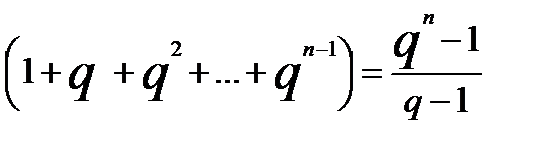 .
.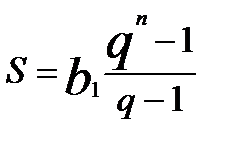
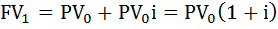
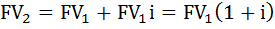 , а так как
, а так как  мы уже вычислили, заменим её и получим
мы уже вычислили, заменим её и получим 
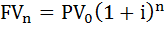
 денег под i процентов годовых на n лет.
денег под i процентов годовых на n лет. , то первая функция денег означает накопление денег от единичного, то есть одноразового вклада денег, допустим на депозит, и как будет выглядеть первоначальное вложение, то есть в какую сумму превратиться оно и выглядит эта формула так:
, то первая функция денег означает накопление денег от единичного, то есть одноразового вклада денег, допустим на депозит, и как будет выглядеть первоначальное вложение, то есть в какую сумму превратиться оно и выглядит эта формула так: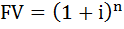


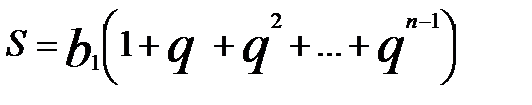
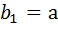 ,
, 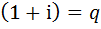 . А так как:
. А так как: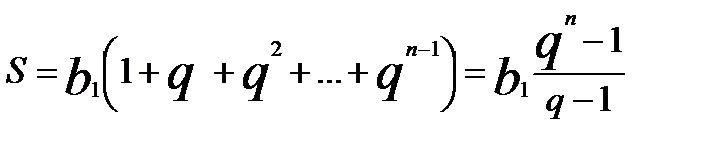

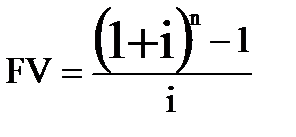

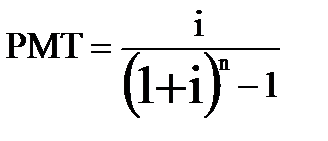 .
.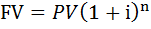 , этот процесс называется наращивание или компаудинг. То обратный процесс, когда нам известна будущая стоимость, ну например, мы хотим накопить 1 долл через n лет, сколько нужно вложить сейчас под i процентов годовых? Этот процесс уже называется дисконтирование. С этой формулы, легко вывести неизвестное нам PV:
, этот процесс называется наращивание или компаудинг. То обратный процесс, когда нам известна будущая стоимость, ну например, мы хотим накопить 1 долл через n лет, сколько нужно вложить сейчас под i процентов годовых? Этот процесс уже называется дисконтирование. С этой формулы, легко вывести неизвестное нам PV:





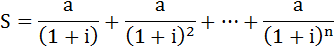
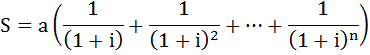
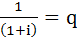 .
.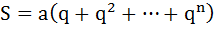
 отдельно, чтобы не запутаться. Теперь, давайте, прибавим единичку и сразу же отнимем, в общем, ничего не поменяется, но за то мы получим следующее выражение:
отдельно, чтобы не запутаться. Теперь, давайте, прибавим единичку и сразу же отнимем, в общем, ничего не поменяется, но за то мы получим следующее выражение:
 , тогда общая формула будет выглядеть так
, тогда общая формула будет выглядеть так 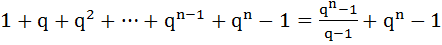 .
.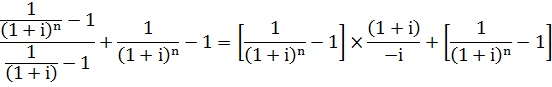
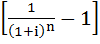 и получим:
и получим:
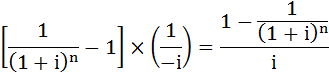
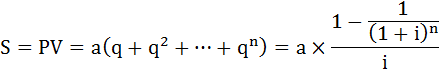
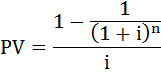

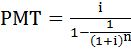 .
.




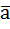 . Либо заглавными латинскими буквами, где первая буква показывает начало отрезка, а вторая буква конец отрезка -
. Либо заглавными латинскими буквами, где первая буква показывает начало отрезка, а вторая буква конец отрезка -  .
.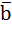 . Чтобы их сложить нужно, как бы соединить их, то есть к концу одного вектора
. Чтобы их сложить нужно, как бы соединить их, то есть к концу одного вектора  Сначала вектор нашего перемещения был вектор
Сначала вектор нашего перемещения был вектор  , только окольными путями. Вот этот вектор
, только окольными путями. Вот этот вектор 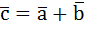 . Думаю, это логично!
. Думаю, это логично!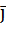 и
и  или ортами:
или ортами: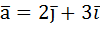 . Это и удобно визуализировать и логично и имеет глубокий смысл:
. Это и удобно визуализировать и логично и имеет глубокий смысл:


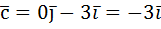 ;
; 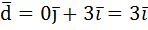 .
.

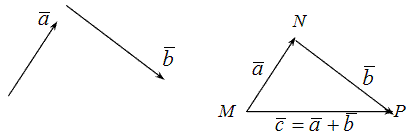
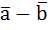 находится от обратного, нужно построить такой вектор, что
находится от обратного, нужно построить такой вектор, что  :
:
 У вектора
У вектора 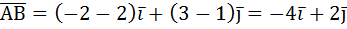 - это и есть координаты самого вектора!
- это и есть координаты самого вектора!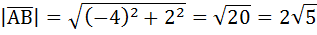
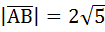 .
.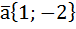 и
и  , давайте сложим эти два вектора через координаты, вычтем вектор
, давайте сложим эти два вектора через координаты, вычтем вектор 
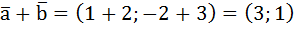 то есть при сложении векторов их координаты складываются, думаю это логично и понятно особенно это чётко видно на изображении слева.
то есть при сложении векторов их координаты складываются, думаю это логично и понятно особенно это чётко видно на изображении слева. 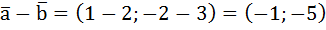 при вычитании координаты вычитаются. При умножении все координаты умножаются на число.
при вычитании координаты вычитаются. При умножении все координаты умножаются на число. Теперь, давайте, познаем и выведем формулу скалярного произведения векторов. Допустим, у нас есть два вектора
Теперь, давайте, познаем и выведем формулу скалярного произведения векторов. Допустим, у нас есть два вектора 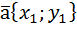 и
и  .
. . У нас есть треугольник OAB, по теореме косинусов, зная длину двух отрезков и угол между ними, можно легко посчитать противоположную углу сторону.
. У нас есть треугольник OAB, по теореме косинусов, зная длину двух отрезков и угол между ними, можно легко посчитать противоположную углу сторону.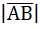 :
:
 , и если мы возьмём квадрат, то используя бином Ньютона и алгебраические свойства модулей, получим:
, и если мы возьмём квадрат, то используя бином Ньютона и алгебраические свойства модулей, получим:
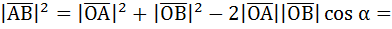
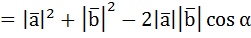
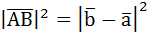 , то получим:
, то получим: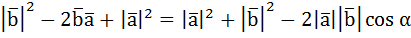
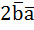 отправим в правую сторону равенства, а всё что справа от знака равно на левую часть, тогда получим:
отправим в правую сторону равенства, а всё что справа от знака равно на левую часть, тогда получим:
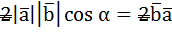 , после сокращения получилось скалярное произведение векторов:
, после сокращения получилось скалярное произведение векторов:
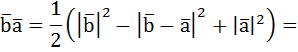
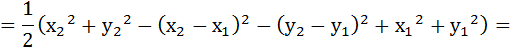
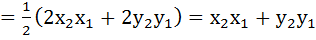 .
. Если параллелограмм поделить с помощью диагонали на две части, у нас получится два одинаковых треугольника. Найдём площадь одного треугольника и умножим на два.
Если параллелограмм поделить с помощью диагонали на две части, у нас получится два одинаковых треугольника. Найдём площадь одного треугольника и умножим на два.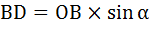 , а сторона
, а сторона 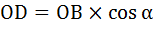 . Тогда площадь треугольника ODB:
. Тогда площадь треугольника ODB: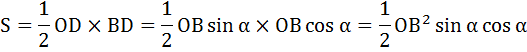


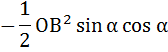
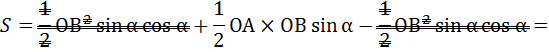
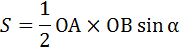
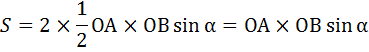
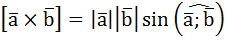 .
. Как и во всём, в теории чисел действует принцип «матрёшки». И эта матрёшка уходит вглубь до бесконечности, повторяя собой модель бесконечной вселенной. А мы своим трёхмерным умом, иногда четырёхмерным, можем пока видеть несколько порядков чисел, и соотвественно с этим видением строить технологии, станки, машины, дома, бизнесы, выстраивать и конструировать ценные бумаги и т.п.
Как и во всём, в теории чисел действует принцип «матрёшки». И эта матрёшка уходит вглубь до бесконечности, повторяя собой модель бесконечной вселенной. А мы своим трёхмерным умом, иногда четырёхмерным, можем пока видеть несколько порядков чисел, и соотвественно с этим видением строить технологии, станки, машины, дома, бизнесы, выстраивать и конструировать ценные бумаги и т.п.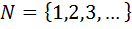 . Натуральные числа делятся на простые и составные числа в свою очередь. Натуральные числа всегда положительны.
. Натуральные числа делятся на простые и составные числа в свою очередь. Натуральные числа всегда положительны.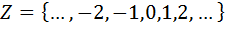 .
.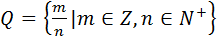 . По сути, говоря рациональное число – это дробь, и появилось оно, когда человеку понадобилось делить некое целое число (в виде объёма, площади, дохода и прочее) на несколько кусков или долей. Обычно результатом дроби является целое число, либо десятичное число, например:
. По сути, говоря рациональное число – это дробь, и появилось оно, когда человеку понадобилось делить некое целое число (в виде объёма, площади, дохода и прочее) на несколько кусков или долей. Обычно результатом дроби является целое число, либо десятичное число, например:  , либо периодическая десятичная дробь, к примеру, число
, либо периодическая десятичная дробь, к примеру, число  , здесь число три, после запятой повторяется бесконечно. Дроби бывают правильные и неправильные.
, здесь число три, после запятой повторяется бесконечно. Дроби бывают правильные и неправильные.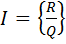 . Иррациональное число включает в себя множество всех выше, рассмотренных чисел, и все они вместе составляют множество вещественных или как ещё говорят множество действительных чисел R. Иррациональное число – можно представить в виде дроби, результатом которого является бесконечное непериодическое десятичное число, или извлечь корень. Из всех множеств, именно иррациональные числа являются самыми загадочными, например такие знаменитые числа:
. Иррациональное число включает в себя множество всех выше, рассмотренных чисел, и все они вместе составляют множество вещественных или как ещё говорят множество действительных чисел R. Иррациональное число – можно представить в виде дроби, результатом которого является бесконечное непериодическое десятичное число, или извлечь корень. Из всех множеств, именно иррациональные числа являются самыми загадочными, например такие знаменитые числа: 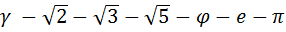 . Интересны они тем, что мы отобразить их на числовой прямой можем, лишь приближённо. Так как, только округлив, мы можем их отобразить, а так оно стремится к некому числу бесконечно, но никогда не достигнет его J
. Интересны они тем, что мы отобразить их на числовой прямой можем, лишь приближённо. Так как, только округлив, мы можем их отобразить, а так оно стремится к некому числу бесконечно, но никогда не достигнет его J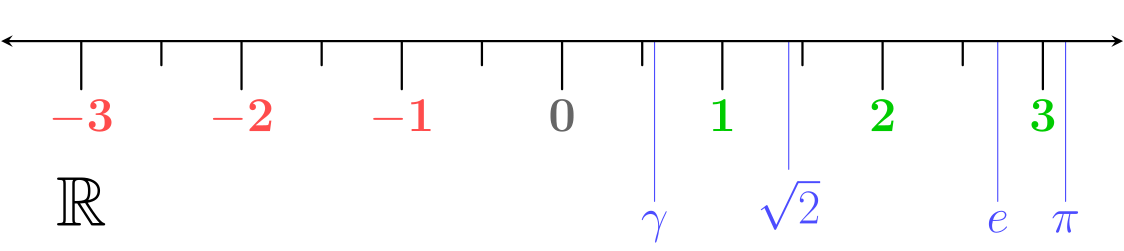
 , на оси вещественных чисел не имеет решение, но на самом деле решение есть, и оно приходит с другого измерения. Да-да, так оно и есть, только назвали это число мнимой единицей и обозначили как
, на оси вещественных чисел не имеет решение, но на самом деле решение есть, и оно приходит с другого измерения. Да-да, так оно и есть, только назвали это число мнимой единицей и обозначили как 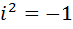 .
.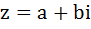 , где
, где 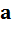 – это множество вещественных чисел, а
– это множество вещественных чисел, а 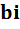 - множество мнимых единиц.
- множество мнимых единиц. А так как комплексное число возникает с другого измерения, то его отображают в виде вектора, при этом вещественную часть числа откладывают по горизонтальной оси вещественных чисел, а мнимую часть откладывают по вертикальной оси мнимых единиц, а сам вектор направлен с нуля на пересечение этих множеств.
А так как комплексное число возникает с другого измерения, то его отображают в виде вектора, при этом вещественную часть числа откладывают по горизонтальной оси вещественных чисел, а мнимую часть откладывают по вертикальной оси мнимых единиц, а сам вектор направлен с нуля на пересечение этих множеств.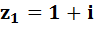 - на картинке слева чёрным цветом мы отобразили вектор этого числа, далее просто по цвету, вы найдёте вектор комплексного числа…
- на картинке слева чёрным цветом мы отобразили вектор этого числа, далее просто по цвету, вы найдёте вектор комплексного числа… 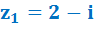 ;
;  ;
; 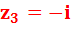 ;
; 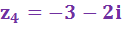 ;
; 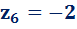 .
.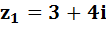 и
и 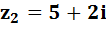 .
.
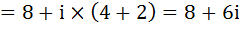
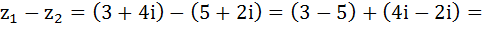
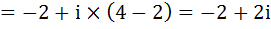

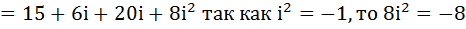
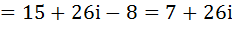
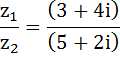

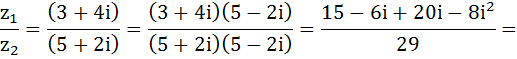
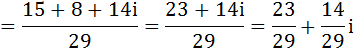

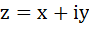 – отобразим это число на числовой оси. По оси X будем отображать вещественные числа, по оси Y мнимые единицы. Как мы уже знаем, что любое комплексное число представляет собой вектор, который разлагается на вещественную часть и мнимую, отобразим этот вектор r на картинке выше. Синяя жирная точка – это и есть комплескное число z. Вектор r одновременно можно представить и как радиус окружности с углом φ.
– отобразим это число на числовой оси. По оси X будем отображать вещественные числа, по оси Y мнимые единицы. Как мы уже знаем, что любое комплексное число представляет собой вектор, который разлагается на вещественную часть и мнимую, отобразим этот вектор r на картинке выше. Синяя жирная точка – это и есть комплескное число z. Вектор r одновременно можно представить и как радиус окружности с углом φ.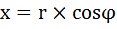 , а мнимую часть через синус угла:
, а мнимую часть через синус угла: 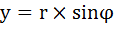 .
.


