Итак, используя векторные диаграммы, мы вывели немало формул, но до сих пор так и не сказали, а что же представляют собой оси, в которых мы эти диаграммы строим? Давайте поговорим об осях. Это так называемая комплексная плоскость, но чтобы понять, что такое комплексная плоскость, поговорим сперва о том, какие бывают числа. Числа бывают натуральные: 1, 2, 3, 4 и так далее, до бесконечности. С натуральными числами можно делать различные операции, например, операцию сложения: 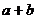 . Результатом будет вновь натуральное число. Можно делать операцию умножения:
. Результатом будет вновь натуральное число. Можно делать операцию умножения:  . Результат – вновь натуральное число. А вот с вычитанием проблема: может получиться натуральное число, а может, и нет. Так, если от 5 отнять 7, не получится натурального числа. Что же делать? Перейдем от натуральных чисел к более общему множеству – к целым числам, все целые числа, от минус бесконечности до плюс бесконечности. Теперь мы можем сколько угодно складывать, умножать и вычитать целые числа – результатом всегда будут целые числа. А вот с делением возникает проблема. Если разделить одно целое число на другое, результат может оказаться целым числом, а может, и нет. Так, если 8 разделить на 3, результат не является целым числом. Поэтому расширяем множество дальше и получаем множество рациональных чисел. Это множество чисел вида
. Результат – вновь натуральное число. А вот с вычитанием проблема: может получиться натуральное число, а может, и нет. Так, если от 5 отнять 7, не получится натурального числа. Что же делать? Перейдем от натуральных чисел к более общему множеству – к целым числам, все целые числа, от минус бесконечности до плюс бесконечности. Теперь мы можем сколько угодно складывать, умножать и вычитать целые числа – результатом всегда будут целые числа. А вот с делением возникает проблема. Если разделить одно целое число на другое, результат может оказаться целым числом, а может, и нет. Так, если 8 разделить на 3, результат не является целым числом. Поэтому расширяем множество дальше и получаем множество рациональных чисел. Это множество чисел вида  , где
, где 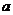 и
и 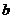 - целые числа (и
- целые числа (и 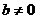 ). Теперь мы можем складывать, умножать, вычитать и делить рациональные числа сколько угодно – результат будет вновь рациональным числом. Проблема возникает, когда мы извлекаем квадратный корень (пока что из положительного числа). Так, квадратный корень из 2 нельзя представить в виде дроби
). Теперь мы можем складывать, умножать, вычитать и делить рациональные числа сколько угодно – результат будет вновь рациональным числом. Проблема возникает, когда мы извлекаем квадратный корень (пока что из положительного числа). Так, квадратный корень из 2 нельзя представить в виде дроби  , где
, где 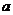 и
и 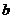 - целые числа. Расширяемся дальше и получаем множество алгебраических чисел – это числа, которые могут быть корнями уравнения
- целые числа. Расширяемся дальше и получаем множество алгебраических чисел – это числа, которые могут быть корнями уравнения 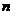 -ной степени:
-ной степени: 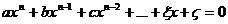 , где
, где 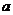 ,
, 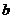 , …,
, …,  - целые коэффициенты. Так, квадратный корень из 2 является корнем уравнения
- целые коэффициенты. Так, квадратный корень из 2 является корнем уравнения 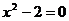 , а кубический корень из 7 – корнем уравнения
, а кубический корень из 7 – корнем уравнения 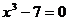 . Теперь мы можем складывать, умножать, вычитать, делить, возводить в целую и дробную степень, извлекать корень целой и дробной степени из алгебраических чисел – результат будет алгебраическим числом (примечание: пока что еще нельзя извлекать корень четной степени из отрицательного числа). Какие-то алгебраические числа рациональные, какие-то иррациональные. Однако существуют числа, не являющиеся алгебраическими, то есть, не являющиеся корнями какого-либо уравнения
. Теперь мы можем складывать, умножать, вычитать, делить, возводить в целую и дробную степень, извлекать корень целой и дробной степени из алгебраических чисел – результат будет алгебраическим числом (примечание: пока что еще нельзя извлекать корень четной степени из отрицательного числа). Какие-то алгебраические числа рациональные, какие-то иррациональные. Однако существуют числа, не являющиеся алгебраическими, то есть, не являющиеся корнями какого-либо уравнения 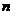 -ной степени. Например, десятичный логарифм любого натурального числа (кроме чисел вида
-ной степени. Например, десятичный логарифм любого натурального числа (кроме чисел вида 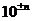 ),
),  ,
,  и
и  для любого ненулевого алгебраического
для любого ненулевого алгебраического  , ну и числа
, ну и числа 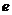 и
и  . Хотя и есть предположение, что число
. Хотя и есть предположение, что число  - рациональное, а число
- рациональное, а число  - целое, но то и другое не доказано, но даже если это так,
- целое, но то и другое не доказано, но даже если это так,  всё равно не есть корень полиномного уравнения, то есть, не алгебраическое число. Расширяем множество чисел дальше, и получаем множество вещественных чисел. Вещественные числа, не являющиеся алгебраическими, называются трансцендентными. И все трансцендентные числа иррациональны.
всё равно не есть корень полиномного уравнения, то есть, не алгебраическое число. Расширяем множество чисел дальше, и получаем множество вещественных чисел. Вещественные числа, не являющиеся алгебраическими, называются трансцендентными. И все трансцендентные числа иррациональны.
Теперь мы можем складывать, вычитать, умножать, делить, возводить в степень (в том числе не целую), извлекать корень, искать логарифм, вычислять тригонометрические функции от вещественных чисел – результат почти всегда будет вновь вещественным числом. Но все-таки почти, то есть, не всегда!
Вещественные числа образуют так называемую вещественную ось, от минус бесконечности до плюс бесконечности. И свободных промежутков между ними нет. Кажется, что расширить числовое множество уже больше некуда. Любая операция, как кажется, должна вновь приводить к вещественному числу: так число  плюс число
плюс число 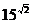 будет число
будет число 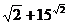 , все числа вещественные.
, все числа вещественные.

| Однако, чему равен квадратный корень из минус единицы? Давайте разберемся. У нас есть вещественная ось. Какое число, при возведении его в квадрат, даст минус единицу? Похоже, такого числа на вещественной оси нет… Поступим уже знакомым нам способом – расширим числовое множество. Но куда его дальше расширять? Мы уже вплотную заняли всю ось, расширяться некуда… А вот и нет: заняли ось, расширяемся на второе измерение, то есть, на плоскость. А как расширяться? Во-первых, обозначим 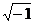 как как  - мнимая единица. Её отложим на оси, перпенди-кулярной вещественной оси. Это так называемая - мнимая единица. Её отложим на оси, перпенди-кулярной вещественной оси. Это так называемая
|
| мнимая ось. Вещественную ось обозначим 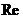 , а мнимую ось обозначим , а мнимую ось обозначим  . .
Любая точка на этой так называемой комплексной плоскости соответствует так называемому комплексному числу:
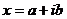 , где , где  , , 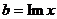
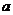 и и 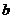 - вещественные числа. - вещественные числа.
В качестве примера, решим квадратное уравнение  . Оно точно имеет два решения. А вот какие? Дискриминант: . Оно точно имеет два решения. А вот какие? Дискриминант:
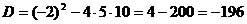
И тогда
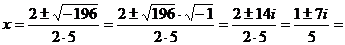
| 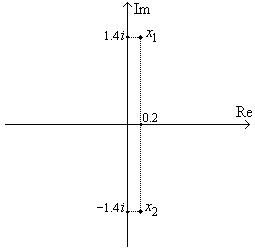
|
| | | |
 . Итак, у нас два решения,
. Итак, у нас два решения, 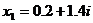 и
и  . Где эти решения? Их нет на вещественной оси. Но они есть на комплексной плоскости. Почему сперва казалось, что решений у уравнения нет? Точнее, почему говорят, что если дискриминант отрицательный, то решений нет? Потому что их нет на вещественной оси. Но они есть вне этой оси, на комплексной плоскости.
. Где эти решения? Их нет на вещественной оси. Но они есть на комплексной плоскости. Почему сперва казалось, что решений у уравнения нет? Точнее, почему говорят, что если дискриминант отрицательный, то решений нет? Потому что их нет на вещественной оси. Но они есть вне этой оси, на комплексной плоскости.
С комплексными числами (подмножеством которых, кстати, являются вещественные числа) мы можем теперь проделывать абсолютно любые операции – и результат вновь будет комплексным числом. Можно, конечно, расширить множество чисел и дальше, выйти за пределы плоскости и получить гиперкомплексные числа, но этого нам здесь не требуется.



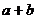 . Результатом будет вновь натуральное число. Можно делать операцию умножения:
. Результатом будет вновь натуральное число. Можно делать операцию умножения:  . Результат – вновь натуральное число. А вот с вычитанием проблема: может получиться натуральное число, а может, и нет. Так, если от 5 отнять 7, не получится натурального числа. Что же делать? Перейдем от натуральных чисел к более общему множеству – к целым числам, все целые числа, от минус бесконечности до плюс бесконечности. Теперь мы можем сколько угодно складывать, умножать и вычитать целые числа – результатом всегда будут целые числа. А вот с делением возникает проблема. Если разделить одно целое число на другое, результат может оказаться целым числом, а может, и нет. Так, если 8 разделить на 3, результат не является целым числом. Поэтому расширяем множество дальше и получаем множество рациональных чисел. Это множество чисел вида
. Результат – вновь натуральное число. А вот с вычитанием проблема: может получиться натуральное число, а может, и нет. Так, если от 5 отнять 7, не получится натурального числа. Что же делать? Перейдем от натуральных чисел к более общему множеству – к целым числам, все целые числа, от минус бесконечности до плюс бесконечности. Теперь мы можем сколько угодно складывать, умножать и вычитать целые числа – результатом всегда будут целые числа. А вот с делением возникает проблема. Если разделить одно целое число на другое, результат может оказаться целым числом, а может, и нет. Так, если 8 разделить на 3, результат не является целым числом. Поэтому расширяем множество дальше и получаем множество рациональных чисел. Это множество чисел вида  , где
, где 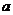 и
и 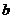 - целые числа (и
- целые числа (и 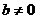 ). Теперь мы можем складывать, умножать, вычитать и делить рациональные числа сколько угодно – результат будет вновь рациональным числом. Проблема возникает, когда мы извлекаем квадратный корень (пока что из положительного числа). Так, квадратный корень из 2 нельзя представить в виде дроби
). Теперь мы можем складывать, умножать, вычитать и делить рациональные числа сколько угодно – результат будет вновь рациональным числом. Проблема возникает, когда мы извлекаем квадратный корень (пока что из положительного числа). Так, квадратный корень из 2 нельзя представить в виде дроби 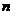 -ной степени:
-ной степени: 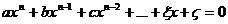 , где
, где  - целые коэффициенты. Так, квадратный корень из 2 является корнем уравнения
- целые коэффициенты. Так, квадратный корень из 2 является корнем уравнения 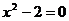 , а кубический корень из 7 – корнем уравнения
, а кубический корень из 7 – корнем уравнения 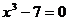 . Теперь мы можем складывать, умножать, вычитать, делить, возводить в целую и дробную степень, извлекать корень целой и дробной степени из алгебраических чисел – результат будет алгебраическим числом (примечание: пока что еще нельзя извлекать корень четной степени из отрицательного числа). Какие-то алгебраические числа рациональные, какие-то иррациональные. Однако существуют числа, не являющиеся алгебраическими, то есть, не являющиеся корнями какого-либо уравнения
. Теперь мы можем складывать, умножать, вычитать, делить, возводить в целую и дробную степень, извлекать корень целой и дробной степени из алгебраических чисел – результат будет алгебраическим числом (примечание: пока что еще нельзя извлекать корень четной степени из отрицательного числа). Какие-то алгебраические числа рациональные, какие-то иррациональные. Однако существуют числа, не являющиеся алгебраическими, то есть, не являющиеся корнями какого-либо уравнения 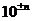 ),
),  ,
,  и
и  для любого ненулевого алгебраического
для любого ненулевого алгебраического  , ну и числа
, ну и числа 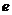 и
и  . Хотя и есть предположение, что число
. Хотя и есть предположение, что число  - рациональное, а число
- рациональное, а число  - целое, но то и другое не доказано, но даже если это так,
- целое, но то и другое не доказано, но даже если это так,  плюс число
плюс число 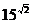 будет число
будет число 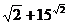 , все числа вещественные.
, все числа вещественные.
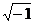 как
как  - мнимая единица. Её отложим на оси, перпенди-кулярной вещественной оси. Это так называемая
- мнимая единица. Её отложим на оси, перпенди-кулярной вещественной оси. Это так называемая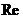 , а мнимую ось обозначим
, а мнимую ось обозначим  .
.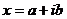 , где
, где  ,
, 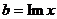
 . Оно точно имеет два решения. А вот какие? Дискриминант:
. Оно точно имеет два решения. А вот какие? Дискриминант: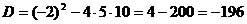
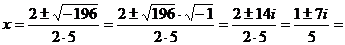
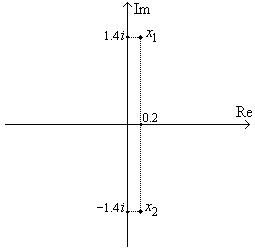
 . Итак, у нас два решения,
. Итак, у нас два решения, 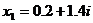 и
и  . Где эти решения? Их нет на вещественной оси. Но они есть на комплексной плоскости. Почему сперва казалось, что решений у уравнения нет? Точнее, почему говорят, что если дискриминант отрицательный, то решений нет? Потому что их нет на вещественной оси. Но они есть вне этой оси, на комплексной плоскости.
. Где эти решения? Их нет на вещественной оси. Но они есть на комплексной плоскости. Почему сперва казалось, что решений у уравнения нет? Точнее, почему говорят, что если дискриминант отрицательный, то решений нет? Потому что их нет на вещественной оси. Но они есть вне этой оси, на комплексной плоскости.

