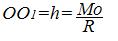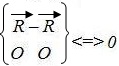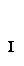Случай 1. Пусть дана произвольная система сил, для которой второй инвариант отличен от нуля: ( RM0) ≠ 0, а следовательно, и первый инвариант отличен от нуля:
R ≠ 0.
Раскладываем главный момент на две составляющие: по направлению главного вектора и перпендикулярно главному вектору.
По существу пару с моментом M 0 раскладываем на две пары с моментами M 1П и M 2П, M 0 = M 1П + M 2П (рис.36).
Для пары с моментом M 2П подберем плечо таким образом, чтобы модуль сил пары был равен модулю главного вектора. Это можно сделать на основании третьей теоремы об эквивалентных парах. На основании второй теоремы об эквивалентных парах эту пару повернем в ее плоскоститак, чтобы одна из сил пары была направлена прямо противоположно главному вектору, т.е. пару с моментом M 2П представим так
R - R
OO

На основании второй аксиомы статики система сил
На основании третьей аксиомы статики ее можно отбросить. Таким образом, в этом случае произвольная система сил эквивалентна одной силе R и паре с моментом M 1П, коллинеарным силе R.
Запишем приведенное доказательство
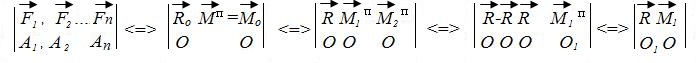
Определение 1. Совокупность силы и пары, момент которой коллинеарен силе, называется динамой или динамическим винтом.
По определению MП = pR, где p- параметр динамы.
Различают правуюдинаму p>0 (рис.37) и левую динаму p<0 (рис.38).

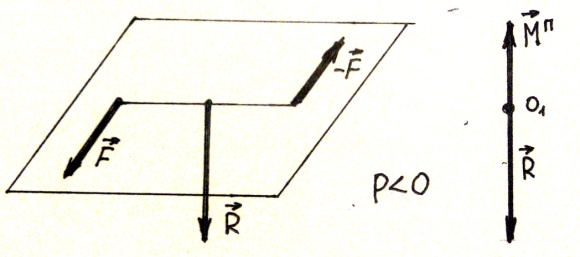
Рис.37 Рис.38
Определение 2. Центральной осью произвольной системы сил называется геометрическое место центров приведения, относительно которых главный момент коллинеарен главному вектору или равен нулю.
MN = pR.
Согласно этому определению точка О1 принадлежит центральной оси. Если взять любую точкуN, которая находится на линии действия главного вектораR, проходящего через точку О1, то эта точка N  также будет принадлежать центральной оси, так как главный момент относительно этой
также будет принадлежать центральной оси, так как главный момент относительно этой
точки будет равен
M N = M 0 - MП2.
Следовательно, если второй инвариант произвольной системы сил отличен от нуля, то такая система сил приводится к динаме, расположенной вдоль центральной оси.
Уравнение центральной оси произвольной системы сил
При приведении произвольной системы сил к точке О мы получили главный векторR и пару с моментом MП = M 0.
Выберем систему координат О XYZ.
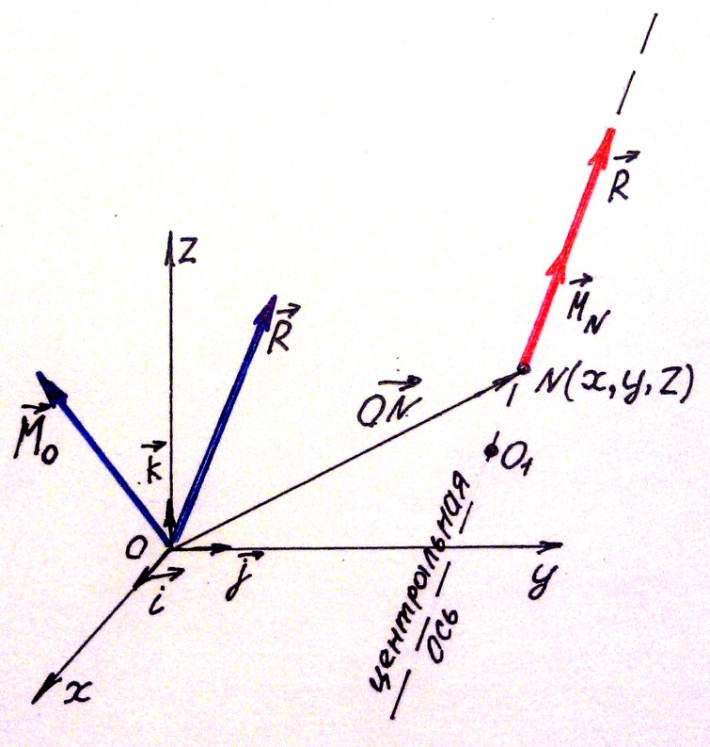
Рис.39
Возьмём произвольную точку N(x,y,z)на центральной оси (рис.39). Из определения центральной оси следует M N= pR. Запишем зависимость между главными моментами произвольной пространственной системы сил относительно двух точек O и N.
M o = M N +[ ON ∙ R ], откуда MN = M o -[ ON ∙ R ].
С другой стороны, M N = PR, следовательно, Mo-[ ON ∙ R] = pR,
где Mo = M x i + M y j + M z k.
Векторное произведениеи [ NO ∙ R ] запишем в виде символического определителя третьего порядка
ij k
M x i + M y j + M z k - x y z =pR.
RxRyRz
Спроецируем последнее равенство на оси координат.
M x-(yR z- zR y) = pR x; M y-(zR x- xR z) = pR y; M z-(xR y- yR x) = pR z.
Предполагая, что RX,RY иRZотличны от нуля,и поделив последние равенства соответственно на R X, RY и RZ получим,
 M x-(yR z- zR y) M y-(zR x- xR z) Mz-(xR y- yR x) (30)
M x-(yR z- zR y) M y-(zR x- xR z) Mz-(xR y- yR x) (30)
R x R y R z
Это уравнение является уравнением центральной оси произвольной системы сил.
Случай 2. Пусть произвольная система сил такова, что первый инвариант отличен от нуля, а второй инвариант равен нулю: 
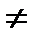 0, (
0, ( 
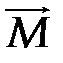
 ) = 0.
) = 0.
Это возможно в двух случаях:
а) M 0 = 0.
 Если M 0 = 0, то система сил эквивалентна одной силе, равной сумме всех сил системы и проходящей через точку О, т.е. система сил приводится к равнодействующей R= F v, проходящей через точку О.
Если M 0 = 0, то система сил эквивалентна одной силе, равной сумме всех сил системы и проходящей через точку О, т.е. система сил приводится к равнодействующей R= F v, проходящей через точку О.
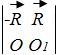 б) M0 ≠ 0, M 0
б) M0 ≠ 0, M 0  R.
R.
Если M 0  R то пару с моментом M 0 можно представить как,
R то пару с моментом M 0 можно представить как,
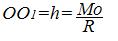
где..
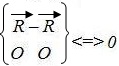
Так как система, то ее можно отбросить. Следовательно, система
сил  будет эквивалентна одной силе, проходящей через точку О 1, т.е. система сил
будет эквивалентна одной силе, проходящей через точку О 1, т.е. система сил
приводится к равнодействующей R = F, проходящей через точку О 1.
Итак, если первый инвариант отличен от нуля, а второй инвариант равен нулю, то произвольная система сил приводится к равнодействующей, расположенной вдоль центральной оси.
Случай 3. Пусть произвольная пространственная система сил такова, что главный вектор равен нулю и главный момент относительно произвольной точки отличен от нуля R = 0, M 0 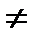 0. Очевидно, что в этом случае система сил приводится к паре сил, причем MП= M 0 .
0. Очевидно, что в этом случае система сил приводится к паре сил, причем MП= M 0 .
Случай 4. Если произвольная пространственная система сил такова, что главный вектор равен нулю и главный момент относительно произвольной точки равен нулю
R=0, M 0=0, то она находится в равновесии. Эти условия будут как достаточными, так и необходимыми для равновесия.
Сводная таблица результатов приведения пространственной системы
сил к простейшему (каноническому) виду




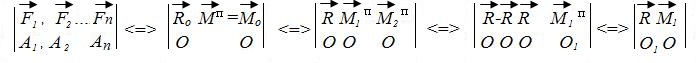


 также будет принадлежать центральной оси, так как главный момент относительно этой
также будет принадлежать центральной оси, так как главный момент относительно этой
 M x-(yR z- zR y) M y-(zR x- xR z) Mz-(xR y- yR x) (30)
M x-(yR z- zR y) M y-(zR x- xR z) Mz-(xR y- yR x) (30)
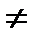 0, (
0, ( 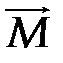
 ) = 0.
) = 0. Если M 0 = 0, то система сил эквивалентна одной силе, равной сумме всех сил системы и проходящей через точку О, т.е. система сил приводится к равнодействующей R= F v, проходящей через точку О.
Если M 0 = 0, то система сил эквивалентна одной силе, равной сумме всех сил системы и проходящей через точку О, т.е. система сил приводится к равнодействующей R= F v, проходящей через точку О.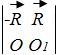 б) M0 ≠ 0, M 0
б) M0 ≠ 0, M 0  R.
R.