Поскольку существует различие в описании распределения непрерывных и дискретных случайных величин, то в изображении и для их аппроксимации применяются различные формулы.
Для непрерывных случайных величин наиболее простым является равномерное (прямоугольное) распределение с двумя параметрами {a, b}, соответствующим границам интервала, внутри которого может находиться случайная величина. Это распределение встречается в основном в двух типовых ситуациях: во-первых, когда в некотором интервале все значения случайной величины равновозможны и, во-вторых, при аппроксимации других непрерывных распределений в относительно малых интервалах.
Равномерное распределение на интервале [a, b] задается плотностью
f (x) = 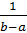
Функция распределения на этом интервале
F(x) = 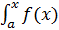 dx=
dx=  =
= 
Условная плотность распределения
λ(t) =  =
= 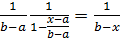 .
.
Математическое ожидание соответствует середине интервала:
mx = 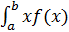 dx =
dx = 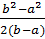 =
= 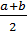 .
.
Дисперсия распределения
Dx = 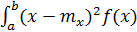 dx =
dx = 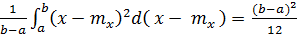 .
.
Графики функции и плотности распределения показаны на рис. 4.1.
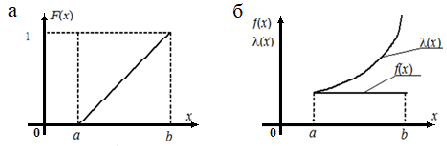
Рис. 4.1. Графики распределения случайной величины по прямоугольному (равномерному) закону:
а – функция распределения;б – плотность распределения
Некоторые случайные величины имеют ЭКСПОНЕНЦИАЛЬНОЕ распределение с одним параметром λ0>0 (однопараметрическое).
Функция распределения
F(x) = 1 - 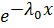 .
.
Плотность распределения
f(x) = 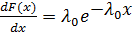 .
.
Условная плотность распределения
λ(x) = 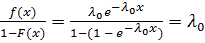 .
.
Закон определен для случайной величины x≠ 0.
Математическое ожидание случайной величины
mx = 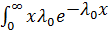 dx =
dx = 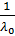 .
.
Дисперсия
Dx = 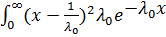 dx =
dx = 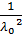 .
.
По экспоненциальному закону, как правило, распределяется случайная величина – продолжительность работы оборудования до отказа, если его отказы не связаны со старением, т.е. износом оборудования, ухудшением определяющих его работоспособность характеристик. Это распределение наблюдается, когда отказы вызываются случайными внешними факторами, например, колебаниями тепловой, электрической или механической нагрузок, изменением качества топлива, особенностями работы различных операторов или другими случайными воздействиями.
Графики функции и плотности экспоненциального распределения показаны на рис. 4.2.
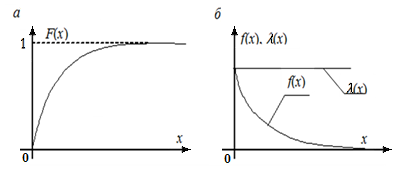
Рис. 4.2. Графики функции (a) и плотности (б) распределения случайной величины по экспоненциальному закону
Наиболее общим является распределение ГАУССА, или НОРМАЛЬНОЕ распределение. Этот закон занимает особое положение. Доказано, что сумма достаточно большого числа независимых или слабо зависимых случайных величин, подчиненных каким угодно законам распределения, приближенно подчиняется нормальному закону распределения. По этой причине нормальный закон распределения наиболее часто встречается в природе. Большинство встречающихся на практике случайных величин, таких как, например, ошибки измерений, могут быть представлены как суммы большого числа малых элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законом распределения ни подчинялись отдельные элементарные ошибки, особенности этих распределений в сумме нивелируются и сумма оказывается подчиненной закону, близкому к нормальному.
Нормальный закон распределения характеризуется плотностью вероятности:
f(x) = 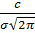 exp [ -
exp [ - 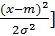 ,
,
при с = 1 имеем:
f (x) = 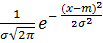 .
.
Кривая плотности распределения по нормальному закону, приведенная на рис. 4.3, имеет симметричный холмообразный вид. Максимальная ордината кривой, равная 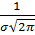 , соответствует точке x=m. По мере удаления от точки x=m плотность распределения падает, и кривая асимптотически прижимается к оси х.
, соответствует точке x=m. По мере удаления от точки x=m плотность распределения падает, и кривая асимптотически прижимается к оси х.
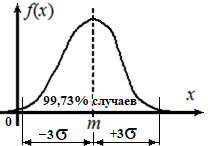
Рис. 4.3. График плотности распределения случайной величины по экспоненциальному закону (распределение Гаусса)
Параметрами распределения являются коэффициенты m и σ. Величина m здесь соответствует математическому ожиданию случайной величины; σ - среднее квадратичное отклонение величины х. Если изменить величину m, то кривая распределения будет смещаться вдоль оси абсцисс, не меняя своей формы. Центр рассеивания характеризует положение распределения на оси абсцисс. Параметр σ характеризует не положение, а саму форму кривой распределения. Это характеристика рассеяния. Необходимо сразу заметить, что в область (-3σ; +3σ) попадает 99,73% значений случайной величины х.
Наибольшая ордината кривой обратно пропорциональна величине σ, чем больше σ, тем ниже максимальное значение f (x). Влияние этих параметров показано на рис. 4.4.
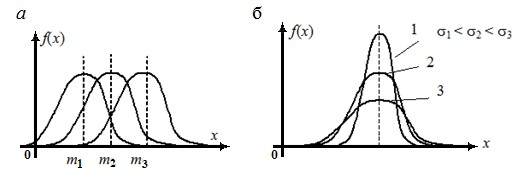
Рис. 4.4. Влияние параметров распределения на координацию и форму плотности распределения Гаусса:
а – математическое ожидание; б – среднеквадратическое отклонение
Во многих задачах, связанных с нормально распределенными случайными величинами, необходимо определить вероятность попадания случайной величины Х в интервал [ α, β ]:
P (α˂ X ˂ β) = F (β) – F (α).
Здесь F(x) – функция распределения величины Х:
F(x) = 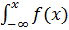 dx =
dx = 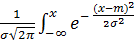 dx.
dx.
Вычисление значения функции распределения требует в каждом случае численного интегрирования. Чтобы избежать этого, используется нормированное нормальное распределение с m = 0 и σ = 1. Для этого вводится новая переменная u:
u = 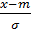 ;
;  u; dx = σdu.
u; dx = σdu.
Функция распределения принимает вид
F (x) = 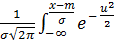 σdu =
σdu = 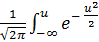 du.
du.
Обычно используется обозначение
Ф(u) = 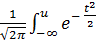 dt.
dt.
Интеграл 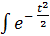 dt не выражается через элементарные функции. Это так называемый интеграл вероятности. Для него составлены таблицы. Поскольку функция Ф(u) симметрична, то Ф(-u) = 1 - Ф(u). Вероятность нахождения случайной величины X в диапазоне [ α, β ] определится выражением
dt не выражается через элементарные функции. Это так называемый интеграл вероятности. Для него составлены таблицы. Поскольку функция Ф(u) симметрична, то Ф(-u) = 1 - Ф(u). Вероятность нахождения случайной величины X в диапазоне [ α, β ] определится выражением
P (α˂ X ˂ β) = Ф( 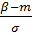 ) – Ф(
) – Ф( 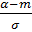 ).
).
В ряде таблиц приводится значение интеграла для 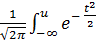 dt. При u=0Ф(u) = 0,5.
dt. При u=0Ф(u) = 0,5.
В том случае, когда случайная величина представляет произведение большого числа независимых случайных величин, среди которых нет преобладающих, то распределение ее вероятности соответствует ЛОГАРИФМИЧЕСКИ НОРМАЛЬНОМУ распределению.
Плотность распределения определяется выражением
f(x) = 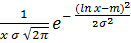
параметр нормированного распределения
u = 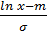 .
.
Закон определен для случайной величины x>0. График плотности распределения показан на рис. 4.5.
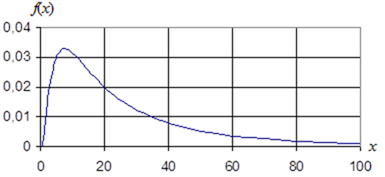
Рис. 4.5. График плотности логарифмически нормального распределения
Это распределение позволяет описать распределение случайной величины, имеющую положительную асимметрию. Нормальное распределение хорошо согласуется с опытными данными, когда количество измерений достаточно велико. При малом количестве измерений более адекватным является распределение СТЬЮДЕНТА. В качестве параметра распределения используется величина
t = 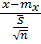 .
.
Плотность вероятности распределения параметра t зависит от величины t и также от числа степеней свободы nс, nс=n-1. Кривые напоминают кривые нормального распределения, но при малых n (или nс) они значительно медленнее сближаются с осью абсцисс. Общий вид этих кривых показан на рис. 4.6.
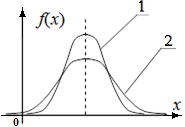
Рис. 4.6. График плотности распределения случайных величин, имеющих нормальное распределение (1) и распределение Стьюдента (2)
При увеличении количества измерений распределение Стьюдента приближается к нормальному распределению. Значения плотности и функции распределения Стьюдента выражаются через гамма-функции, для вычисления которых необходимо численное интегрирование. Поэтому обычно пользуются статистическими таблицами, в которых в зависимости от числа степеней свободы n для нескольких значений уровня значимости a приводятся значения параметра tкр(1), для которого вероятность появления значений t < tкр(1) равна доверительной вероятности b=1-a (односторонний критерий) или tкр(2), для которого вероятность выполнения условия tкр(2)< t < tкр(2) равна b (двухсторонний критерий).
Применительно к описанию усталости металлов Вейбуллом предложено распределение, называемое распределением ВЕЙБУЛЛА, функция распределения вероятности которого имеет вид:
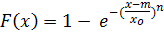 .
.
Плотность распределения
f(x) = 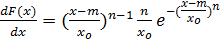 .
.
Закон определен при x > m, x0 > 0. Распределение имеет три параметра: m,x0 и n. Параметр m соответствует характеристике положения случайной величины, параметр x0 нормирует значение случайной величины и определяет степень рассеяния. Параметр n определяет вид (форму) кривой плотности распределения и также оказывает влияние на рассеяние случайной величины. При 0< n 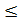 1 график плотности представляет собой L- образную кривую, при n >0 кривая принимает колоколообразный вид. При m =0 и n =1 распределение Вейбулла переходит в экспоненциальное распределение. Характерный вид кривых показан на рис. 4.7.
1 график плотности представляет собой L- образную кривую, при n >0 кривая принимает колоколообразный вид. При m =0 и n =1 распределение Вейбулла переходит в экспоненциальное распределение. Характерный вид кривых показан на рис. 4.7.
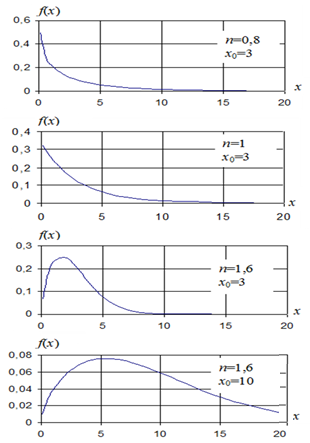
Рис. 4.7. Графики плотности распределения для закона Вейбулла
В отличие от нормального, распределение Вейбулла не имеет математического обоснования и является только достаточно хорошей аппроксимацией опытных данных. Вейбулл отмечал, что единственным достоинством этого распределения является простота математического выражения при выполнении необходимых общих условий. Опыт показывает, что во многих случаях это распределение лучше описывает некоторые наблюдения, чем другие известные функции.
Для представления непрерывных случайных величин используются также другие виды распределений, в частности χ2-распределение Пирсона, F-распределение Фишера и т.д. Расчетные формулы или значения функций распределения приводятся в табличном виде в справочной литературе.



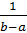
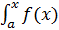 dx=
dx=  =
= 
 =
= 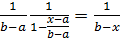 .
.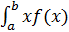 dx =
dx = 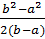 =
= 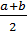 .
.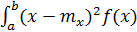 dx =
dx = 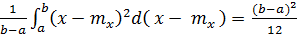 .
.
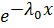 .
.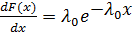 .
.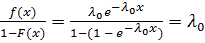 .
.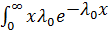 dx =
dx = 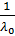 .
.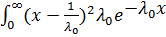 dx =
dx = 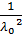 .
.
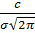 exp [ -
exp [ - 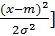 ,
,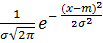 .
.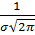 , соответствует точке x=m. По мере удаления от точки x=m плотность распределения падает, и кривая асимптотически прижимается к оси х.
, соответствует точке x=m. По мере удаления от точки x=m плотность распределения падает, и кривая асимптотически прижимается к оси х.

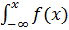 dx =
dx = 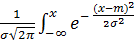 dx.
dx.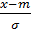 ;
;  u; dx = σdu.
u; dx = σdu.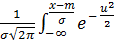 σdu =
σdu = 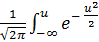 du.
du.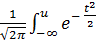 dt.
dt.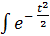 dt не выражается через элементарные функции. Это так называемый интеграл вероятности. Для него составлены таблицы. Поскольку функция Ф(u) симметрична, то Ф(-u) = 1 - Ф(u). Вероятность нахождения случайной величины X в диапазоне [ α, β ] определится выражением
dt не выражается через элементарные функции. Это так называемый интеграл вероятности. Для него составлены таблицы. Поскольку функция Ф(u) симметрична, то Ф(-u) = 1 - Ф(u). Вероятность нахождения случайной величины X в диапазоне [ α, β ] определится выражением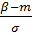 ) – Ф(
) – Ф( 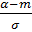 ).
).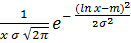
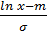 .
. 
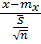 .
.
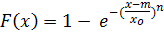 .
.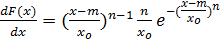 .
.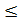 1 график плотности представляет собой L- образную кривую, при n >0 кривая принимает колоколообразный вид. При m =0 и n =1 распределение Вейбулла переходит в экспоненциальное распределение. Характерный вид кривых показан на рис. 4.7.
1 график плотности представляет собой L- образную кривую, при n >0 кривая принимает колоколообразный вид. При m =0 и n =1 распределение Вейбулла переходит в экспоненциальное распределение. Характерный вид кривых показан на рис. 4.7.



