Дата: 07.02.2022
| Предмет
| Учитель
| Задание на урок
| Домашнее задание
| |
| Алгебра
| Давыдова И.А.
| Повторить теоретический материал стр. 117-120( или конспект в тетради). Изучить материал. Сделать конспект.
| Выучить конспект. Стр.122-126 изучить. Стр. 125 записать правило в синей рамке. Выполнить письменно № 534(первый столбик)
| |
|
В тетрадях:
7 февраля
Дистанционная работа
Формула корней квадратного уравнения
Теоретическая часть. Изучить, сделать краткий конспект. Переписать и разобрать примеры
Квадратные уравнения можно решать методом выделения квадрата двучлена.
Напомним формулы квадрата разности и квадрата суммы.
a2 + 2ab + b2 = (a + b)2
a2 – 2ab + b2 = (a – b)2
Рассмотрим уравнение 5x2 – 6x + 1 = 0.
Преобразуем к приведённому виду. Разделим на 5 обе части уравнения:
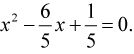
Второй коэффициент представим в виде произведения:
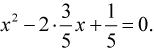
Для выделения квадрата двучлена не хватает квадрата вычитаемого. Прибавим выражение 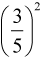 к разности и, чтобы ничего не изменилось, вычтем его же:
к разности и, чтобы ничего не изменилось, вычтем его же:
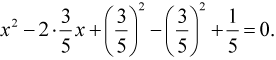
Преобразуем уравнение в квадрат двучлена:
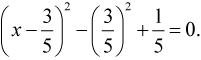
Перенеся слагаемые таким образом, чтобы в левой части был квадрат разности, а справа от знака равенства находилось свободное число, получим:
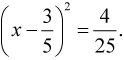
Извлечение корня из квадрата приводит к двум линейным уравнениям:
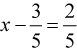 или
или 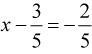 .
.
В итоге получим x = 1 или x = 0,2.
Алгоритм решение квадратного уравнения в общем виде
ax2 + bx + c = 0, a ≠ 0.
Деление на первый коэффициент квадратного трёхчлена – получение приведённого квадратного уравнения:
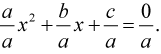
Получение уравнения вида – квадрат многочлена слева, свободное число справа:
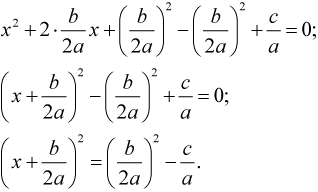
Приведение к общему знаменателю:
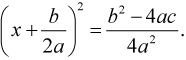
Число корней этого уравнения зависит от знака правой части.
4a2 > 0, значит, знак дроби зависит от знака выражения b2 – 4ac.
Записать обязательно!
D = b2 – 4ac.
D – дискриминант.
Возможны три случая.
1. D = b2 – 4ac < 0.
Значит и уравнение не имеет действительных корней.
2. D = b2 – 4ac = 0.
Уравнение принимает вид 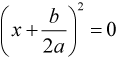 , очевидно, что
, очевидно, что 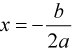 . Т. е. квадратное уравнение имеет один корень.
. Т. е. квадратное уравнение имеет один корень.
3. D = b2 – 4ac > 0.
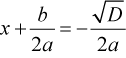 или
или 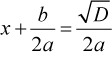 .
.
Получим два корня:
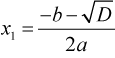 или
или 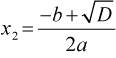 .
.
На все вопросы отвечу по номеру телефона.
Все ответы на задания присылать на электронный адрес:
Давыдова И.А. - alekseevna675@gmail.com
Также можно делать фото выполненных заданий и отправлять в личные сообщения в соцсети VK.
| Учитель
| электронный адрес
| Соцсети
|
| Давыдова И.А.
| alekseevna675@gmail.com
| VK https://vk.com/hell_hound666
|



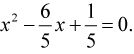
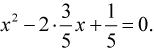
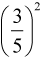 к разности и, чтобы ничего не изменилось, вычтем его же:
к разности и, чтобы ничего не изменилось, вычтем его же: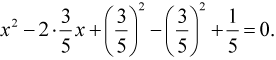
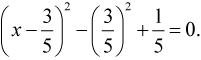
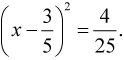
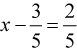 или
или 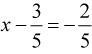 .
.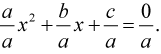
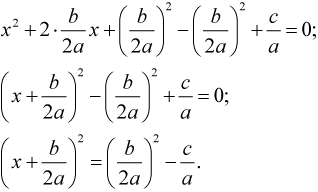
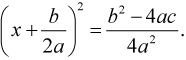
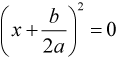 , очевидно, что
, очевидно, что 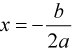 . Т. е. квадратное уравнение имеет один корень.
. Т. е. квадратное уравнение имеет один корень.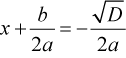 или
или 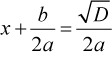 .
.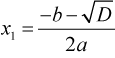 или
или 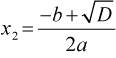 .
.

