Урок-лекция
Задание: изучить материал и ответить на контрольные вопросы.
Тема: «Понятие криволинейной трапеции. Площадь криволинейной трапеции. Понятие определенного интеграла. Свойства определенного интеграла. Формула Ньютона-Лейбница».
Цель урока:
ввести понятие определенного интеграла, криволинейной трапеции, рассмотреть свойства определённого интеграла и формулу Ньютона-Лейбница.
Ход урока.
1. Изучение нового материала
Рассмотрим фигуру изображенную на рис.1. Снизу фигура ограничена осью абсцисс, с боков прямыми х=а и х=b, а сверху графиком функции f непрерывной и неотрицательной на отрезке [а; b]. Такую фигуру называют криволинейной трапецией.
Рассмотрим задачу.
 Задача 1. В декартовой прямоугольной системе координат хОу дана фигура, ограниченная осью х, прямыми х = а, х = b (а < b) и графиком непрерывной и неотрицательной на отрезке [а;b] функции у=f(x). Требуется вычислить площадь этой фигуры.
Задача 1. В декартовой прямоугольной системе координат хОу дана фигура, ограниченная осью х, прямыми х = а, х = b (а < b) и графиком непрерывной и неотрицательной на отрезке [а;b] функции у=f(x). Требуется вычислить площадь этой фигуры.
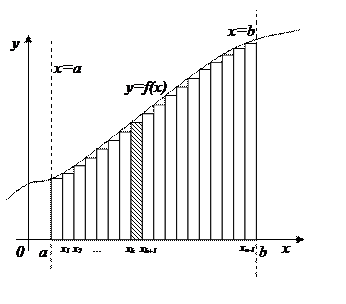 Найдем, используя геометрические соображения, приближенное значение площади. Для этого разобьем отрезок [а;b] (основание криволинейной трапеции) на n равных частей с помощью точек
Найдем, используя геометрические соображения, приближенное значение площади. Для этого разобьем отрезок [а;b] (основание криволинейной трапеции) на n равных частей с помощью точек 

 , …,
, …,  ,
, 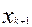 ,…,
,…, 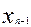 . Проведем соответствующие ординаты. Криволинейная трапеция разбилась на n частей – на n узеньких столбиков. Площадь трапеции будет равна сумме площадей столбиков.
. Проведем соответствующие ординаты. Криволинейная трапеция разбилась на n частей – на n узеньких столбиков. Площадь трапеции будет равна сумме площадей столбиков.
Рассмотрим отдельно k-тый столбик, т.е. криволинейную трапецию, основанием которой служит отрезок [  ;
; 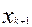 ]. Заменим его прямоугольником с тем же основанием и высотой, равной f(
]. Заменим его прямоугольником с тем же основанием и высотой, равной f( ). Площадь прямоугольника равна
). Площадь прямоугольника равна 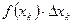 , где
, где 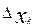 -длина отрезка [
-длина отрезка [  ;
; 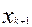 ]. Мы получили приближенное значение площади k-го столбика.
]. Мы получили приближенное значение площади k-го столбика.
Площадь S заданной криволинейной трапеции приближенно равна площади 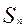 ступенчатой фигуры, составленной из n прямоугольников (рис.2):
ступенчатой фигуры, составленной из n прямоугольников (рис.2):
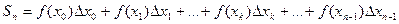
Считаем, что 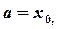 ,
, 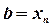 .Приближенное равенство
.Приближенное равенство  тем точнее, чем больше n.
тем точнее, чем больше n.
Принято считать, что искомая площадь криволинейной трапеции равна пределу последовательности (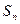 ):
):  .
.
Можно доказать, что этот предел существует. Его называют определенным интегралом от функции у= f(х) по отрезку [а; b] и обозначают так:  ;
;
читают: интеграл от а до b эф от икс дэ икс. Числа а и b называют пределами интегрирования (соответственно нижним и верхним)
Вернемся к задаче и запишем: S= 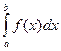 ;
;
здесь S – площадь криволинейной трапеции. В этом состоит геометрический смысл определенного интеграла.
Масса неоднородного стержня с плотностью p(x) вычисляется по формуле m= 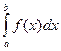 . В этом состоит физический смысл определенного интеграла.
. В этом состоит физический смысл определенного интеграла.
Перемещение s точки, движущейся по прямой со скоростью v(t), за промежуток времени от t=а до t=b, вычисляется по формуле s= 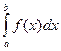 . Это еще одно физическое истолкование определенного интеграла. Для вычисления определённого интеграла воспользуемся теоремой.
. Это еще одно физическое истолкование определенного интеграла. Для вычисления определённого интеграла воспользуемся теоремой.
Теорема. Если функция y= f(x) непрерывна на отрезке [а; b], то справедлива формула 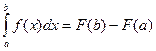 , где F(x) – первообразная для f(x).
, где F(x) – первообразная для f(x).
Эту формулу называют формулой Ньютона – Лейбница.
Урок-лекция
Задание: изучить материал и ответить на контрольные вопросы.
Тема: «Понятие криволинейной трапеции. Площадь криволинейной трапеции. Понятие определенного интеграла. Свойства определенного интеграла. Формула Ньютона-Лейбница».
Цель урока:
ввести понятие определенного интеграла, криволинейной трапеции, рассмотреть свойства определённого интеграла и формулу Ньютона-Лейбница.
Ход урока.
1. Изучение нового материала
Рассмотрим фигуру изображенную на рис.1. Снизу фигура ограничена осью абсцисс, с боков прямыми х=а и х=b, а сверху графиком функции f непрерывной и неотрицательной на отрезке [а; b]. Такую фигуру называют криволинейной трапецией.
Рассмотрим задачу.
 Задача 1. В декартовой прямоугольной системе координат хОу дана фигура, ограниченная осью х, прямыми х = а, х = b (а < b) и графиком непрерывной и неотрицательной на отрезке [а;b] функции у=f(x). Требуется вычислить площадь этой фигуры.
Задача 1. В декартовой прямоугольной системе координат хОу дана фигура, ограниченная осью х, прямыми х = а, х = b (а < b) и графиком непрерывной и неотрицательной на отрезке [а;b] функции у=f(x). Требуется вычислить площадь этой фигуры.
 Найдем, используя геометрические соображения, приближенное значение площади. Для этого разобьем отрезок [а;b] (основание криволинейной трапеции) на n равных частей с помощью точек
Найдем, используя геометрические соображения, приближенное значение площади. Для этого разобьем отрезок [а;b] (основание криволинейной трапеции) на n равных частей с помощью точек 

 , …,
, …,  ,
, 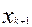 ,…,
,…, 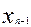 . Проведем соответствующие ординаты. Криволинейная трапеция разбилась на n частей – на n узеньких столбиков. Площадь трапеции будет равна сумме площадей столбиков.
. Проведем соответствующие ординаты. Криволинейная трапеция разбилась на n частей – на n узеньких столбиков. Площадь трапеции будет равна сумме площадей столбиков.
Рассмотрим отдельно k-тый столбик, т.е. криволинейную трапецию, основанием которой служит отрезок [  ;
; 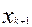 ]. Заменим его прямоугольником с тем же основанием и высотой, равной f(
]. Заменим его прямоугольником с тем же основанием и высотой, равной f( ). Площадь прямоугольника равна
). Площадь прямоугольника равна 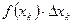 , где
, где 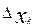 -длина отрезка [
-длина отрезка [  ;
; 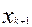 ]. Мы получили приближенное значение площади k-го столбика.
]. Мы получили приближенное значение площади k-го столбика.
Площадь S заданной криволинейной трапеции приближенно равна площади 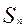 ступенчатой фигуры, составленной из n прямоугольников (рис.2):
ступенчатой фигуры, составленной из n прямоугольников (рис.2):
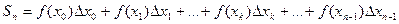
Считаем, что 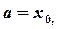 ,
, 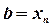 .Приближенное равенство
.Приближенное равенство  тем точнее, чем больше n.
тем точнее, чем больше n.
Принято считать, что искомая площадь криволинейной трапеции равна пределу последовательности (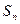 ):
):  .
.
Можно доказать, что этот предел существует. Его называют определенным интегралом от функции у= f(х) по отрезку [а; b] и обозначают так:  ;
;
читают: интеграл от а до b эф от икс дэ икс. Числа а и b называют пределами интегрирования (соответственно нижним и верхним)
Вернемся к задаче и запишем: S= 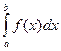 ;
;
здесь S – площадь криволинейной трапеции. В этом состоит геометрический смысл определенного интеграла.
Масса неоднородного стержня с плотностью p(x) вычисляется по формуле m= 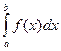 . В этом состоит физический смысл определенного интеграла.
. В этом состоит физический смысл определенного интеграла.
Перемещение s точки, движущейся по прямой со скоростью v(t), за промежуток времени от t=а до t=b, вычисляется по формуле s= 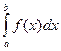 . Это еще одно физическое истолкование определенного интеграла. Для вычисления определённого интеграла воспользуемся теоремой.
. Это еще одно физическое истолкование определенного интеграла. Для вычисления определённого интеграла воспользуемся теоремой.
Теорема. Если функция y= f(x) непрерывна на отрезке [а; b], то справедлива формула 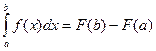 , где F(x) – первообразная для f(x).
, где F(x) – первообразная для f(x).
Эту формулу называют формулой Ньютона – Лейбница.
Рассмотрим свойства определённого интеграла.



 Задача 1. В декартовой прямоугольной системе координат хОу дана фигура, ограниченная осью х, прямыми х = а, х = b (а < b) и графиком непрерывной и неотрицательной на отрезке [а;b] функции у=f(x). Требуется вычислить площадь этой фигуры.
Задача 1. В декартовой прямоугольной системе координат хОу дана фигура, ограниченная осью х, прямыми х = а, х = b (а < b) и графиком непрерывной и неотрицательной на отрезке [а;b] функции у=f(x). Требуется вычислить площадь этой фигуры. Найдем, используя геометрические соображения, приближенное значение площади. Для этого разобьем отрезок [а;b] (основание криволинейной трапеции) на n равных частей с помощью точек
Найдем, используя геометрические соображения, приближенное значение площади. Для этого разобьем отрезок [а;b] (основание криволинейной трапеции) на n равных частей с помощью точек 

 , …,
, …,  ,
,  ,…,
,…, 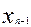 . Проведем соответствующие ординаты. Криволинейная трапеция разбилась на n частей – на n узеньких столбиков. Площадь трапеции будет равна сумме площадей столбиков.
. Проведем соответствующие ординаты. Криволинейная трапеция разбилась на n частей – на n узеньких столбиков. Площадь трапеции будет равна сумме площадей столбиков.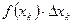 , где
, где 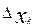 -длина отрезка [
-длина отрезка [ 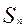 ступенчатой фигуры, составленной из n прямоугольников (рис.2):
ступенчатой фигуры, составленной из n прямоугольников (рис.2):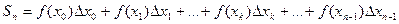
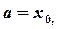 ,
, 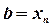 .Приближенное равенство
.Приближенное равенство  тем точнее, чем больше n.
тем точнее, чем больше n.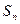 ):
):  .
. ;
;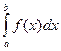 ;
;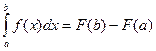 , где F(x) – первообразная для f(x).
, где F(x) – первообразная для f(x).


