Постановка задачи неравномерного кодирования

 

Предположим, что для некоторого дискретного источника X с известным распределением вероятностей {p(x), xÎX} требуется построить эффективный неравномерный двоичный код над алфавитом A = {a}. Как и ранее, мы сосредоточим внимание на двоичных кодах, т.е. мы предполагаем, что A = {0,1}. Дело в том, что, во-первых, все идеи в полной мере иллюстрируются на этом примере. Во-вторых, обобщение на случай произвольного алфавита не представляет никакой трудности.

В качестве примера источника рассмотрим алфавит русского языка. Сразу же вспоминается азбука Морзе, которая сопоставляет каждой букве комбинацию точек «•» и тире «-». Например, часто встречающейся букве «е» соответствует комбинация «•», а более редкой букве «ч» соответствует комбинация «- - - •». Однако, мы не получим хорошего кода просто заменив точки нулями, а тире – единицами. Нам будет не хватать пауз, разделяющих буквы (3 точки), пауз, разделяющих слова (7 точек). По сути дела код Морзе – это недвоичный код.

Нам необходим такой двоичный код, который допускает однозначное разделение последовательности кодовых слов на отдельные кодовые слова без использования каких-либо дополнительных символов. Это требование называют свойством однозначной декодируемости.

Неравномерный побуквенный код C = { } объема |C| = N над алфавитом A определяется как произвольное множество последовательностей одинаковой или различной длины из букв алфавита A. Код является однозначно декодируемым, если любая последовательность символов из A единственным способом разбивается на отдельные кодовые слова.

 

Пример 12.1. Для источника X = {0, 1, 2, 3} среди четырех кодов

 

a)C₁ = {00, 01, 10, 11};

b)C₂ = {1, 01, 001, 000};

c)C₃ = {1, 10, 100, 000};

d) C₄ = {0, 1, 10, 01};

первые три кода однозначно декодируемы, последний код – нет.

Первый код этого примера – равномерный код. Понятно, что любой равномерный код может быть однозначно декодирован.

Для декодирования второго кода можно применить следующую стратегию. Декодер считывает символ за символом, и каждый раз проверяет, не совпадает ли полученная последовательность с одним из кодовых слов. В случае успеха соответствующее сообщение выдается получателю, и декодер приступает к декодированию следующего сообщения. В случае кода C₂ неоднозначности не может быть, поскольку ни одно слово не является продолжением другого.

Если ни одно кодовое слово не является началом другого, код называется префиксным. Префиксные коды являются однозначно декодируемыми.

Код C₃ заведомо не префиксный. Тем не менее, мы утверждаем, что он – однозначно декодируемый. Каждое слово кода C₃ получено переписыванием в обратном порядке соответствующего слова кода C₂. Для декодирования последовательности кодовых слов кода C₃ можно переписать принятую последовательность в обратном порядке и для декодирования использовать декодер кода C₂. Таким образом, мы приходим к следующему выводу.

Префиксность – достаточное, но не необходимое условие однозначной декодируемости.

Графически удобно представлять префиксные коды в виде кодовых деревьев. В частности, кодовое дерево кода C₂ примера 12.1. представлено на рис.12.1.

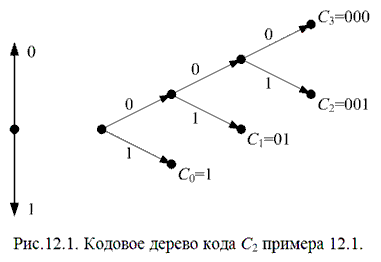
Узлы дерева размещаются на ярусах. На начальном (нулевом) ярусе расположен узел, называемый корнем дерева. Узлы следующих ярусов связаны с узлами предыдущих ярусов ребрами. Ребрам приписаны кодовые символы. Таким образом, каждой вершине дерева соответствует последовательность, считываемая вдоль пути, связывающего данный узел с корнем дерева.

Узел называется концевым, если из него не исходит ни одного ребра. Код называют древовидным, если в качестве кодовых слов он содержит только кодовые слова, соответствующие концевым вершинам кодового дерева.

Древовидность кода и префиксность – синонимы в том смысле, что всякий древовидный код является префиксным, и всякий префиксный код может быть представлен с помощью кодового дерева. Мы будем рассматривать только префиксные коды. В связи с этим возникает вопрос: не потеряли ли мы, оптимальное решение задачи, сузив класс кодов, среди которых мы ищем наилучшие? Ниже мы убедимся в том, что ответ на этот вопрос отрицательный.

Обсудим теперь, какие именно префиксные коды считать хорошими. Наша цель неравномерного кодирования состоит в уменьшении затрат на передачу сообщений, логично выбрать в качестве критерия качества кода среднюю длину кодовых слов. Рассмотрим источник X = {1, …, N}, который порождает буквы с вероятностями {P₁, …, P_N}. Предположим, что для кодирования букв источника выбран код  с длинами кодовых слов length( ₁) = m₁,..., length( _N) =m_N соответственно. Средней длиной кодовых слов называется величина

.

Пример 12.2. Рассмотрим источник и коды из примера 12.1. Подсчитайте среднюю длину кодовых слов кодов C₁ и C₂ для трех распределений вероятностей на буквах источника:

a) P₀ = P₁ = P₂ = P₃ = 1/4;

b) P₀ = 1/2; P₁ = 1/4: P₂ = P₃ = 1/8;

c) P₀ = P₁ = 1/8: P₂ = 1/4; P₃ = 1/2.

Результаты расчетов показывают, что не всегда и не любой неравномерный код эффективен. Еще один немаловажный аспект, который должен быть учтен при сравнении способов неравномерного кодирования, это сложность реализации кодирования и декодирования, а также сложность построения или модификации кода при изменении статистических данных об источнике.

Подводя итог, мы формулируем задачу побуквенного неравномерного кодирования как задачу построения однозначно декодируемого кода с наименьшей средней длиной кодовых слов при заданных ограничениях на сложность.

Неравенство Крафта

Вернемся к примеру 12.1 и сравним коды C₁ и C₂ объема 4. Код C₁ равномерный, все слова имеют одинаковую длину 2. Нельзя ли выбрать слова короче? Действительно, в коде C₂ есть одно слово длины 1, но чтобы сохранить объем кода и префиксность, пришлось на единицу увеличить длины двух других кодовых слов. Этот пример показывает, что требование префиксности накладывает жесткие ограничения на множество длин кодовых слов и не дает возможности выбирать кодовые слова слишком короткими. Формально эти ограничения записываются в виде изящного неравенства, называемого неравенством Крафта.

Теорема 12.1. Необходимым и достаточным условием существования префиксного кода объема N с длинами кодовых слов m₁,…,m_N является выполнение неравенства

                      (12.1)

Для достижения равенства в (12.1) кодовое дерево должно быть полным, т.е. каждая промежуточная вершина дерева должна иметь ровно 2 потомка и всем концевым вершинам должны быть сопоставлены кодовые слова.

Неравенство Крафта как бы ограничивает снизу длины кодовых слов префиксного кода заданного объема N. В связи с этим важно быть уверенным, что оно имеет место и для любых других однозначно декодируемых кодов. Это утверждение является содержанием следующей теоремы.

Теорема 12.2. Для любого однозначно декодируемого двоичного кода объема N с длинами кодовых слов m₁,…,m_N справедливо неравенство

.                             (12.2)