Понятие вероятности события.

Частота события

Чтобы найти вероятность, как мы помним, нужно количество благоприятных исходов разделить на общее количество исходов. Точно так же находится и частота события, задания на которую так же есть в прототипах. В чем же отличие? Вероятность – это прогнозируемая величина, а частота – констатация состоявшегося факта

Вы научились находить и частоту события. Теперь научимся находить разницу между частотой и вероятностью одного и того же события.

 

«Спрятанные» и «лишние» условия в заданиях

Вы еще не забыли, что задачи надо внимательно читать? Бывает так, что в задаче числа прописаны необычно, в виде текста. И с такими заданиями тоже надо научиться справляться

Но бывают и более сложные задания. Из которых труднее вычленить условия.

Задачи на четность и делимость

Понемножку повышаем сложность заданий, вы еще не устали? Тогда в путь!. Теперь нам надо вспомнить, что такое четные числа, что такое «число делится на 2,3,5,9» и т.д. И еще вспомнить, что двузначных чисел 90 (от 10 до 99 включая), а трехзначных 900 (с 100 до 999 включительно). Эта информация нам нужна в ряде заданий в качестве Nобщ. Итак, разбираемся в примерах.

Задачи с перебором вариантов

Задания с монетами и матчами.

Оооо, столько нелюбимые ребятами задачи с монетами, кубиками и прочим! Решать их можно несколькими способами, но мы выберем самый… наглядный, что ли. Метод перебора вариантов. Но в данном методе нужно быть предельно внимательным, чтобы не упустить ни одного варианта! А то расчеты окажутся неверными.

Аналогичным способом решаются и задачи на матчи (жребий определяет, какая команда будет начинать игру). Нужно тоже перебрать варианты: Задачи на кубики (игральные кости)

Ох, уж эти кубики! Сколько слез было пролито над этими задачками!. А все потому, что в условие каждой из них приходится вникать, понимая, что же в этот раз от нас хотят составители. В этих задачках встречается редкий вопрос, мы о нем говорили в самом начале: найти не саму вероятность, а лишь число благоприятных исходов. Но мы так привыкли подставлять Nбл в формулу, что совершенно не представляем, что именно это значение и может быть ответом!

Хорошо, с благоприятными исходами разобрались, теперь можно понемножку усложнять. Опираясь на принцип перебора, который только что разобрали, решим следующий пример: В рассмотренных примерах мы могли выписать все возможные исходы, и это было нашим Nобщ. Но так бывает далеко не всегда, тут надо очень точно понимать, когда перебирать слишком трудоемко. Что же делать с таким типом задач? Уф, с двумя кубиками справились! Хотя тут было непросто. С тремя будет еще интереснее! Сложный перебор вариантов

 Бывает и так, что в задании с ходу не разобраться, что нужно перебирать варианты. Да и в принципе не понятно, с какого бока приступать к ее выполнению! Одна из таких задач, с которой традиционно возникают сложности, рассмотрена в примере ниже.

В данном примере перебирать нужно было всего 6 вариантов. Но их бывает ЗНАЧИТЕЛЬНО больше. Например, задача по монеты в карманах. Она может решаться и другими способами, но перебором нагляднее и чуточку проще. ЗАКОНЫ ВЕРОЯТНОСТИ

  Несовместные события и закон сложения

 Для того чтобы перейти к рассмотрению более сложных заданий, необходимо ввести новые понятия: независимые события и несовместные события. События являются несовместными, если появление одного события исключает появление другого. Предположим, вы подошли к остановке, от которой только что отъехал автобус, номер которого вы не заметили. Если это отъехал автобус №1, то это никак не мог быть автобус №2 одновременно. В применении к прототипам ЕГЭ: если Вы вытянули билет, в котором только 1 вопрос, касающийся бактерий, то этот же вопрос никак не может коснуться грибов, например. То есть, события «вытянуть билет с вопросом о грибах» и «вытянуть билет с вопросом о бактериях» являются несовместными, ибо появление одного из этих событий исключает появление другого. Вот с этими самыми несовместными событиями дело как раз обстоит очень просто. Если нам надо найти вероятность наступления ИЛИ одного, ИЛИ другого несовместного события, то мы просто складываем вероятности данных событий: р=р1+р2 Несовместные события образуют полную группу событий, суммарная вероятность которой равна 1.

ВАЖНО! Вероятность НЕ наступления события. Раз уж мы научились складывать вероятности, необходимо понять, что сумма вероятностей группы несовместных событий равна 1. Что это значит? Это значит, к примеру, что если вероятность купить бракованное стекло в примере 1 была 0,03, то вероятность купить НЕ бракованное стекло равна р=1-0,03=0,97

Этот случай был достаточно простым. А если в таблицу придется внести больше данных? Рассмотрим в примере ниже. Независимые события и закон умножения

А что же тогда независимые события? Логично, что если появление одного события не исключает появление другого, но и не повышает вероятность появления, то эти события независимы. Например, событие А «Катя дошла до школы» и событие В «Катя купила тетрадь» вполне себе могут иметь место в один и тот же день, пусть и в разное время. От того, дошла ли до школы Катя, не зависит, купит ли она тетрадь. Ну, или нам недостаточно условий, чтобы эту зависимость провести. Будем считать эти события независимыми. В применение к прототипам ЕГЭ независимыми событиями можно считать получение высоких баллов по разным предметам ЕГЭ. Пусть без математики физику, например, хорошо не напишешь, но в рамках теории вероятности будем считать получение оценок по разным предметам событиями независимыми. Здесь можно было бы ввести и формулу для независимых событий, но, как показала практика, ученики начинают путаться в этих формулах.

 

Закон умножения (закон и) (для независимых событий) А что же делать, если нам необходимо найти вероятность наступления И одного события, И другого? Правильно! Логично их перемножить, раз уж функцию сложения мы использовали в прошлом разделе. Следовательно, вероятность наступления И первого, И второго, И третьего независимых события находится по формуле: р=р1*р2*р3

 

 

Ответ: 0,98

 Пример 32. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Решение: Это задание решается непросто. Действительно, если бы эти события были независимыми, то вероятность того, что кофе закончится в обоих автоматах была бы результатом перемножения вероятности того, что кофе закончится в одном из. Но мы видим, что это не так (0,3*0,3 ≠ 0,12). Значит, все то, что мы узнали выше, нам здесь не поможет, нужен какой-то другой метод. Не буду вас томить сложными объяснениями и объяснять, почему решается именно так, расскажу просто механизм решения конкретно этого задания.

Сначала мы находим вероятность наступления двух совместных событий (это понятие мы не вводили) «Кофе закончится в обоих автоматах». Эта вероятность равна сумме вероятностей наступления этих событий без вероятности их совместного наступления:

 р1=0,3+0,3-0,12=0,48

Ответ: 0,52

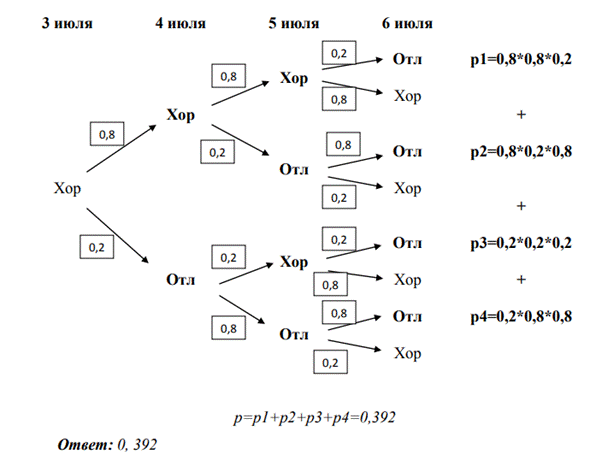
Пример 33: В Волшебной стране бывает два типа погоды: хорошая и отличная, причѐм погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.

Решение: Составим схему всех возможных событий и укажем вероятность наступления данного события. Вероятность того, что произойдет И первое, И второе, И третье – результат умножения вероятность отдельных событий. Вероятность того, что нас устроит один из вариантов, равна сумме получившихся вероятностей.

Пример 34: Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.

 Решение: Команда может получить не меньше 4 очков в двух играх тремя способами: 3+1, 1+3, 3+3. Эти события несовместны, вероятность их суммы равна сумме их вероятностей. Каждое из этих событий представляет собой произведение двух независимых событий — результата в первой и во второй игре. Отсюда имеем: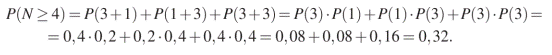

От вет: 0,32.

Пример 35: При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?

Ответ: 5

ПОНЯТИЕ ВЕРОЯТНОСТИ СОБЫТИЯ.

  Классическое определение вероятности

Итак, что же такое вероятность события? Думаю, в повседневной практике вы нередко говорите фразы: «100%, что я приду», «Процентов 70%, что меня не будет». Именно в эти моменты вы уже оперируете понятием «вероятность». Вероятность принято обозначать латинской буквой «р». Это безразмерная величина, у нее нет единицы измерения. Как же ее найти? Если мы рассмотрим выше приведенные примеры, то для того, чтобы определить вероятность, нам необходимо данные в процентах разделить на 100%.

Соответственно, меньше, чем 0% быть не может, и больше, чем 100% быть не может Значит, вероятность находится в пределе 𝑝 ∈ 0; 1.То есть, если вы в примере получили значение вероятности, выходящей из этой области значений, ищите ошибку в вычислениях или ходе мыслей.

При этом р=0 в том случае, если событие не может наступить ни при каких условиях. Например, вероятность события «Луна через 10 секунд упадет на Землю» равна 0. Потому что даже если рассматривать событие «Луна упадет на Землю» как потенциально возможное, то ограничение по времени предполагает, что уже в данные секунды были бы такие значительные катаклизмы, которые не позволили бы нам спокойно сидеть и читать этот текст.

 Р=1, если событие состоится при любых условиях. Например, если вы в классе с парты уроните ручку, она с вероятностью р=1 упадет, а не взлетит или окажется в состоянии невесомости.

 В большинстве задач, которые вы решали ранее, в том числе, в ОГЭ, вычисление вероятности сводилось к нахождению значения по классической формуле вероятности:

Не удивляйтесь, нам в этой задаче не пришлось искать вероятность. Да-да, и такие задачи в ЕГЭ встречаются, будьте внимательны!.

 В большинстве же случаев необходимо найти именно вероятность. Посмотрим на примере, как это делать.

Большинство проблем в заданиях на вероятность связано отнюдь не с незнанием формулы, а с неумением читать. Ну серьезно, ребята, куда вы спешите, решая первую часть? Не бегите вперед батьки в пекло, ваша поспешность может дорогого стоить. Так обидно терять баллы из-за коварной частички «не» (или «на» вместо «из») в вопросе, которую вы «по невнимательности» пропустили. Не спешите, прошу вас! Поучимся читать;)?

«Порядок определяется жеребьевкой»

ВАЖНО! Если в условии задачи сказано, что порядок определяется жребием, жеребьевкой, в случайном порядке, то нам совершенно не важно, каким там по счету должен выступать спортсмен или профессор. Просто «забываем» эту информацию, как лишнюю, добавленную «чтобы запутать». «М. будет выступать шестым» – случайное событие, и оно равновероятное относительно другого порядка выступлений. Расшифрую последнюю фразу: вероятность того, что этот конкретный человек окажется шестым по счету не отличается от вероятности того, что он же будет начинать эту конференцию или соревнования. А раз вероятности этих событий одинаковые, события называются равновероятными. А находим вероятность мы по той же классической формуле. Кажется сложным? Решать проще!

Иногда попадаются задачи с чуть более сложными вычислениями, где, опять же, надо внимательно-внимательно читать. Разберем на следующем примере:

Частота события

Чтобы найти вероятность, как мы помним, нужно количество благоприятных исходов разделить на общее количество исходов. Точно так же находится и частота события, задания на которую так же есть в прототипах. В чем же отличие? Вероятность – это прогнозируемая величина, а частота – констатация состоявшегося факта

Вы научились находить и частоту события. Теперь научимся находить разницу между частотой и вероятностью одного и того же события.

 

«Спрятанные» и «лишние» условия в заданиях

Вы еще не забыли, что задачи надо внимательно читать? Бывает так, что в задаче числа прописаны необычно, в виде текста. И с такими заданиями тоже надо научиться справляться

Но бывают и более сложные задания. Из которых труднее вычленить условия.

Задачи на четность и делимость

Понемножку повышаем сложность заданий, вы еще не устали? Тогда в путь!. Теперь нам надо вспомнить, что такое четные числа, что такое «число делится на 2,3,5,9» и т.д. И еще вспомнить, что двузначных чисел 90 (от 10 до 99 включая), а трехзначных 900 (с 100 до 999 включительно). Эта информация нам нужна в ряде заданий в качестве Nобщ. Итак, разбираемся в примерах.

Задачи с перебором вариантов

Задания с монетами и матчами.

Оооо, столько нелюбимые ребятами задачи с монетами, кубиками и прочим! Решать их можно несколькими способами, но мы выберем самый… наглядный, что ли. Метод перебора вариантов. Но в данном методе нужно быть предельно внимательным, чтобы не упустить ни одного варианта! А то расчеты окажутся неверными.

Аналогичным способом решаются и задачи на матчи (жребий определяет, какая команда будет начинать игру). Нужно тоже перебрать варианты: Задачи на кубики (игральные кости)

Ох, уж эти кубики! Сколько слез было пролито над этими задачками!. А все потому, что в условие каждой из них приходится вникать, понимая, что же в этот раз от нас хотят составители. В этих задачках встречается редкий вопрос, мы о нем говорили в самом начале: найти не саму вероятность, а лишь число благоприятных исходов. Но мы так привыкли подставлять Nбл в формулу, что совершенно не представляем, что именно это значение и может быть ответом!

Хорошо, с благоприятными исходами разобрались, теперь можно понемножку усложнять. Опираясь на принцип перебора, который только что разобрали, решим следующий пример: В рассмотренных примерах мы могли выписать все возможные исходы, и это было нашим Nобщ. Но так бывает далеко не всегда, тут надо очень точно понимать, когда перебирать слишком трудоемко. Что же делать с таким типом задач? Уф, с двумя кубиками справились! Хотя тут было непросто. С тремя будет еще интереснее! Сложный перебор вариантов

 Бывает и так, что в задании с ходу не разобраться, что нужно перебирать варианты. Да и в принципе не понятно, с какого бока приступать к ее выполнению! Одна из таких задач, с которой традиционно возникают сложности, рассмотрена в примере ниже.

В данном примере перебирать нужно было всего 6 вариантов. Но их бывает ЗНАЧИТЕЛЬНО больше. Например, задача по монеты в карманах. Она может решаться и другими способами, но перебором нагляднее и чуточку проще. ЗАКОНЫ ВЕРОЯТНОСТИ

  Несовместные события и закон сложения

 Для того чтобы перейти к рассмотрению более сложных заданий, необходимо ввести новые понятия: независимые события и несовместные события. События являются несовместными, если появление одного события исключает появление другого. Предположим, вы подошли к остановке, от которой только что отъехал автобус, номер которого вы не заметили. Если это отъехал автобус №1, то это никак не мог быть автобус №2 одновременно. В применении к прототипам ЕГЭ: если Вы вытянули билет, в котором только 1 вопрос, касающийся бактерий, то этот же вопрос никак не может коснуться грибов, например. То есть, события «вытянуть билет с вопросом о грибах» и «вытянуть билет с вопросом о бактериях» являются несовместными, ибо появление одного из этих событий исключает появление другого. Вот с этими самыми несовместными событиями дело как раз обстоит очень просто. Если нам надо найти вероятность наступления ИЛИ одного, ИЛИ другого несовместного события, то мы просто складываем вероятности данных событий: р=р1+р2 Несовместные события образуют полную группу событий, суммарная вероятность которой равна 1.

ВАЖНО! Вероятность НЕ наступления события. Раз уж мы научились складывать вероятности, необходимо понять, что сумма вероятностей группы несовместных событий равна 1. Что это значит? Это значит, к примеру, что если вероятность купить бракованное стекло в примере 1 была 0,03, то вероятность купить НЕ бракованное стекло равна р=1-0,03=0,97

Этот случай был достаточно простым. А если в таблицу придется внести больше данных? Рассмотрим в примере ниже. Независимые события и закон умножения

А что же тогда независимые события? Логично, что если появление одного события не исключает появление другого, но и не повышает вероятность появления, то эти события независимы. Например, событие А «Катя дошла до школы» и событие В «Катя купила тетрадь» вполне себе могут иметь место в один и тот же день, пусть и в разное время. От того, дошла ли до школы Катя, не зависит, купит ли она тетрадь. Ну, или нам недостаточно условий, чтобы эту зависимость провести. Будем считать эти события независимыми. В применение к прототипам ЕГЭ независимыми событиями можно считать получение высоких баллов по разным предметам ЕГЭ. Пусть без математики физику, например, хорошо не напишешь, но в рамках теории вероятности будем считать получение оценок по разным предметам событиями независимыми. Здесь можно было бы ввести и формулу для независимых событий, но, как показала практика, ученики начинают путаться в этих формулах.

 

Закон умножения (закон и) (для независимых событий) А что же делать, если нам необходимо найти вероятность наступления И одного события, И другого? Правильно! Логично их перемножить, раз уж функцию сложения мы использовали в прошлом разделе. Следовательно, вероятность наступления И первого, И второго, И третьего независимых события находится по формуле: р=р1*р2*р3