Комбинаторы.
Определение:
λ-выражение без свободных переменных называется комбинатором.
Позволяет избавиться от связанных переменных в λ-выражении.
Системы комбинаторов предназначены для выписывания тех же функций, что системы λ-конверсий, но без использования связанных переменных.
Пример. Ia = a
I: λx.x
Kab = a
K: λxy.x
Sabc = ac(bc)
S: λxyz.xz(yz)
Одни комбинаторы можно выражать через другие I = SKK.
Проверим это двумя способами.
1-ый способ:
Определение:
Комбинаторная характеристика – способ передачи информации об объекте в виде правил текстуального преобразования.
SKKa → Ka(Ka) → a
2-ой способ:
┌──↓ ┌─↓
(λxyz.xz(yz))(λxy.x)(λxy.x)→(λyz.(λxy.x)z(yz))(λxy.x)→((xy.z)(yz)→
↑─────────└────┘
→(λyz.z)(λxy.x)→ λz.z
Определение:
Базис формальной системы - минимальный набор объектов этой системы, через который можно с помощью аксиом и правил вывода выразить все остальные объекты формальной системы.
Определение:
Базисом бестиповой комбинаторной логики является набор комбинаторов: К,S и т.д.
Построение комбинаторной логики
Определение:
Комбинаторная логика (КЛ) - часть математической логики, изучающая комбинаторы и их свойства, где функциональная абстракция выражается без использования формальных переменных.
Введем комбинаторную логику как формальную систему:
 1. Алфавит: (,), хi, сi, S, K, I,…
1. Алфавит: (,), хi, сi, S, K, I,…
комбинаторы
2. Комбинаторные термы:
- все переменные являются термами (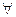 хi – терм);
хi – терм);
- все константы являются термами (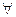 сi - терм);
сi - терм);
- все комбинаторы являются термами (S,K,I,…- термы).
А-терм, В-терм (Если А- терм и В - терм, то аппликация (АВ)-терм)
(AB)-терм Таким образом (АВ) также является термом.
λ-абстракций в комбинаторной логике нет.
Скобки расставляются по ассоциации влево.
3. Правила вывода:


 а→b (μ) a→b (υ ) a→b (τ)
а→b (μ) a→b (υ ) a→b (τ)
ca → cb ac→bc b→c  a→c
a→c
4. Схема аксиом.
Ix → x
Kxy → x
Sxyz → xz(yz)
x → x
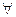 x,y,z
x,y,z
Примеры комбинаторов. Ix = x -тождество
Bxyz = x(yz) - композитор
Wxy = xyy - дупликатор
Cxyz = xzy - пермутатор
Sxyz = xz(yz) - коннектор
Kxy = x - канцелятор
I, B, W, K - также образуют базис.
Определения:
Выражение вида Ix, Kxy, Sxyz называются редексами.
Получившиеся свернутые выражения для редексов (соответственно х, х, xz(yz)) называются контрактами либо сверткой.
Говорят, что выражение А находится в нормальной форме, если оно не содержит редексов. Для любого комбинаторного выражения существует нормальная форма.
Пример
B = S(KS)K
W = SS(K(SKK))
C = S(BBS)(KK)
Теорема Черча-Россера.
If А→В, А→С
then  D:B→D, C→D
D:B→D, C→D
Базис K, S.
Кроме базисного набора K, S будем использовать еще плюс к ним I.
Любое λ-выражение Р, не содержащее свободных переменных представляется в базисе IKS индукцией по построению терма Р.
Р: FV(P) = Ø –свободные переменные.
λх.х = I
λx.P = KP, если х 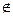 FV(P)
FV(P)
λx.PQ = S(λx.P)(λx.Q)
Примеры.
λxy.yx = S(K(SI))(S(KK)I)
Babc = a(bc) Представим комбинатор B в базисе I,K,S.
B: λxyz.x(yz)
Ый способ
λx.(λy.(λz.x(yz))) = λx.(λy.(S(λz.x)(λz.(yz))) = λx.λy.(S(Kx)(S(λz.y)(λz.z))) =
= λx.λy.((S(Kx)(S(Ky)I)) = λx.(S(λy.S(Kx))(λy.S(Ky))I)) = λx.(S(K(S(Kx)))
(S(λy.S(Ky))(λy.I))) = λx.(S(K(S(Kx)))(S(S(λy.S)(λy.Ky))(KI))) =
= λx.(S(K(S(Kx)))(S(S(KS)(S(KK)I))(KI))) = S(λx.(S(K(S(Kx))))(λx.[…])) =
 нет свободных вхождений х
нет свободных вхождений х
= S(S(λx.S)(λx.K(S(Kx)))(…) = S(S(KS)(S(λx.K)(λx.S(Kx)))(…) =
= (S(S(KS)(S(KK)(S(KS)(λx.Kx))))(…) = (S(S(KS)(S(KK)(S(KK)(I))(…).
Ой способ
a(bc) =(K) Kac(bc) =(S) S(Ka)bc =(K) KSa(Ka)bc =(S) S(KS)Kabc.
Базис I,B,C,S
Для всей комбинаторной логики I,B,C,S не является базисом, т.к. в нем нет укорачивающего правила, которое вводится Kxy = x. Однако для систем без укорачивающих правил I,B,C,S можно использовать как базис.
K – не может быть выражено через остальные комбинаторы, значит для всей комбинаторной логики I,B,C,S - не базис.
Преимущества комбинаторов
Не содержат свободных переменных (не возникает проблемы коллизии переменных).
Убыстряются сами вычисления, которые сводятся к ряду однотипных действий.
Контрольные вопросы
- Дайте определение комбинатора.
- Какие свойства комбинаторов делают удобным их использование для описания аппликативных алгоритмов?
- Дайте определение базиса формальной системы.
- Докажите, что I, B, C, S не является базисом бестиповой комбинаторной логики.
- Приведите определение нумералов и основных операций над ними в рамках бестиповой комбинаторной логики.
- Выразите комбинаторы B, C, W в базисе K, S.
Типизированные системы.
Использование типов.
Типы делают систему более строгой. Если все выражения согласованы по типам, то они реализуются гораздо эффективнее.
Типы назначают вид значения, когда функция прилагается к аргументам.
Предположим, что аппликация имеет тип с, В имеет тип b, тогда А имеет тип b→c.
(АВ)с-тип, Bb Ab→c
Если а,b – типы, то а→b тоже тип.
Пример.
Ix = x
Пусть Ха, тогда Ia→a (т.к. должно выполняться равенство IХа =Ха).
(Kx)y = xα
xα,yβ, то (Kx)α→β
Kxα = Cβ→α, то К α→(β→α)
Sxyz = xz(yz)
Пусть zα, тогда если (yz)β, то уα→β((хz)(уz)β)γ  (xz)β→γ, zα
(xz)β→γ, zα  xα→(β→γ)
xα→(β→γ)
Рассмотрим (Sxyz)γ, zα  (Sxy)α→γ, известно, что уα→β, тогда (Sx)(α→β)→(α→γ)
(Sxy)α→γ, известно, что уα→β, тогда (Sx)(α→β)→(α→γ)
xα→(β→γ), тогда S(α→(β→γ))→((α→β)→(α→γ))
Определение:
Говорят, что тип α приписан комбинатору Х тогда и только тогда, когда это утверждение вытекает из следующих аксиом и правила вывода:
Iα→α
Кα→(β→α)
S (α→(β→γ)) →((α→β)→(α→γ))
Xα→β, Yα
____________________
(XY) β
Обозначения:
Хα или ├#(Х) = α,
├# I = α→ α1.
Пример.
1) Припишем тип аппликации (KI)
Имеем: К α→(β→α) и Iα1→α1. Тогда существует аппликация (KI)β→α, α: α1 → α1.
Тогда (KI) β→(α1→α1)
2) (KI) β→(α→α)bβ→I γ=α→α



 1. Алфавит: (,), хi, сi, S, K, I,…
1. Алфавит: (,), хi, сi, S, K, I,…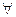 хi – терм);
хi – терм);

 a→c
a→c D:B→D, C→D
D:B→D, C→D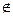 FV(P)
FV(P) нет свободных вхождений х
нет свободных вхождений х


