МОДЕЛИ ГЕТЕРОГЕННЫХ СИСТЕМ
ОСНОВНЫЕ ПОНЯТИЯ И МЕТОДЫ ГИДРОДИНАМИКИ ДИСПЕРСНЫХ СИСТЕМ
В окрестности точки, определяемой радиусом вектором  берем частицу с объемом
берем частицу с объемом 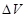 и с общей массой
и с общей массой 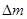 , при этом полагаем, что
, при этом полагаем, что
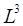 >>
>>  >>
>>  >>
>> 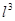
где 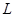 характерный линейный разрез задачи,
характерный линейный разрез задачи, 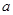 и
и 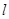 -линейные размеры дисперсных частиц и среднее расстояние между соседними частицами.
-линейные размеры дисперсных частиц и среднее расстояние между соседними частицами.
Для дисперсной системы, состоящей из двух составляющих, можно записать
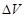 =
= 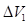 +
+  и
и 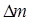 =
= 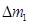 +
+ 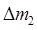 (1.1)
(1.1)
где  и
и 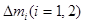 части объема и массы в
части объема и массы в 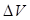 , приходящиеся к
, приходящиеся к
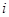 -ой фазе. Введем следующие параметры [1]
-ой фазе. Введем следующие параметры [1]
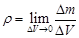 ,
, 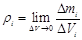 ,
,  (1.2)
(1.2)
 ,
, 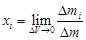 ,
, 
Здесь 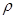 - средняя плотность смеси в целом и
- средняя плотность смеси в целом и  ,
, 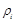 - средние и истинные плотности фаз,
- средние и истинные плотности фаз, 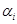 и
и 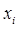 - объемные и массовые содержания (или концентрации) фаз. Очевидно, что из определения этих параметров следует зависимость между ними в виде, используя [1]
- объемные и массовые содержания (или концентрации) фаз. Очевидно, что из определения этих параметров следует зависимость между ними в виде, используя [1]
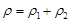 ,
,  ,
, 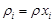 (1.3)
(1.3)
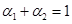 ,
, 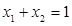
Кроме того, на основе первого соотношения из (1.1) с учетом (1.2) нетрудно получить
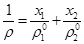 (1.4)
(1.4)
Пусть 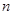 и
и 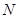 - число дисперсных частиц в единице объема массы дисперсной системы, тогда между этими параметрами имеется следующая связь
- число дисперсных частиц в единице объема массы дисперсной системы, тогда между этими параметрами имеется следующая связь
 (1.5)
(1.5)
Для дальнейшего примем, что дисперсная фаза представляет собой сферические частицы одинакового радиуса  . Тогда имеет место кинематическая связь [1]
. Тогда имеет место кинематическая связь [1]
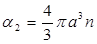 (1.6)
(1.6)
ОДНОСКОРОСТНАЯ МОДЕЛЬ
Уравнения неразрывности. Примем, что составляющие смеси движутся с одинаковыми скоростями (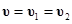 ). Это означает, что в изучаемой проблеме скольжение фаз несущественно. Например, рассматриваются медленные процессы, когда характерные времена задачи
). Это означает, что в изучаемой проблеме скольжение фаз несущественно. Например, рассматриваются медленные процессы, когда характерные времена задачи 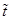 значительно превышают времена релаксации скоростей неравновесности
значительно превышают времена релаксации скоростей неравновесности 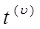 для двухфазной смеси
для двухфазной смеси 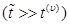 . По аналогии с обычными однофазными системами в этом случае должно иметь место следующее уравнение сохранения массы для всей смеси в целом [1]
. По аналогии с обычными однофазными системами в этом случае должно иметь место следующее уравнение сохранения массы для всей смеси в целом [1]
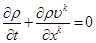 или
или 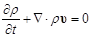 (2.1)
(2.1)
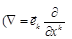 ,
, 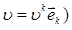
Эти уравнения можно записать, используя
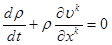 или
или 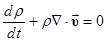 (2.2)
(2.2)
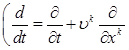 или
или 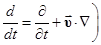

Пусть, в общем случае, может происходить массообмен между составляющими двухфазной системы. Такая ситуация может иметь место, например, в парокапельной смеси. Пар может конденсироваться, или, наоборот, капельки могут испаряться. Введем параметры  и
и  , описывающие интенсивность перехода массы из первой фазы во вторую и, наоборот, из второй фазы в первую. Эти параметры отнесены к единице объема смеси. Тогда для каждой составляющей двухфазной системы можем записать следующие уравнения, выражающие закон сохранения масс [1]
, описывающие интенсивность перехода массы из первой фазы во вторую и, наоборот, из второй фазы в первую. Эти параметры отнесены к единице объема смеси. Тогда для каждой составляющей двухфазной системы можем записать следующие уравнения, выражающие закон сохранения масс [1]
 (2.3)
(2.3)
и
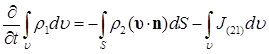
Используя теорему Гаусса-Остроградского, из (2.3) можем получить уравнение неразрывности в форме Эйлера [1]
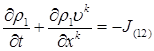 и
и 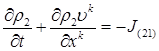 (2.4)
(2.4)
Складывая эти уравнения, получаем уравнение неразрывности (2.1) для всей смеси в целом. При этом необходимо отметить, что введенные параметры для описания межфазного массообмена должны удовлетворять условию

Следовательно, достаточно задавать один из этих параметров  (или
(или 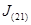 ). Для определенности в последующем примем обозначения
). Для определенности в последующем примем обозначения 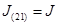 тогда
тогда
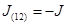 . В случае отсутствия массообмена между фазами имеет место
. В случае отсутствия массообмена между фазами имеет место 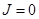 .
.
Запишем уравнение импульсов для первой фазы 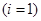 в терминал истинная плотность - объемная концентрация при
в терминал истинная плотность - объемная концентрация при 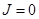 как
как
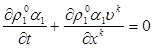 (2.5)
(2.5)
Если это составляющее несжимаемое 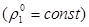 , отсюда следует
, отсюда следует
 (2.6)
(2.6)
В том случае, когда вторая фаза также несжимаема, то аналогично с (2.6) будем иметь
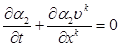 (2.7)
(2.7)
Складывая уравнения (2.6) и (2.7) с учетом 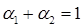 получим
получим
 (2.8)
(2.8)
Таким образом, в случае, когда обе фазы несжимаемые, уравнение неразрывности сводится для поля скоростей к обычному виду для несжимаемой однофазной среды.
Подставляя в уравнение неразрывности среднюю плотность в виде 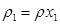 и учитывая уравнение неразрывности для всей смеси в целом (2.1) можем получить:
и учитывая уравнение неразрывности для всей смеси в целом (2.1) можем получить:
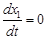 или
или 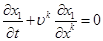 (2.9)
(2.9)
Если предположить, что при течении дисперсной системы не происходит образование и исчезновение дисперсных частиц (отсутствуют процессы дробления или слипания частиц, например), то аналогично с уравнениям неразрывности фаз, можно записать уравнение сохранения числа дисперсных частиц
 (2.10)
(2.10)
Подставляя сюда выражение 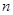 из (1.5) с учетом уравнения неразрывности всей смеси (2.1) получим:
из (1.5) с учетом уравнения неразрывности всей смеси (2.1) получим:
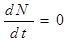 или
или  (2.10)
(2.10)
На основе кинематических зависимостей (1.3) нетрудно получить формулы, связывающие массовые и объемные концентрации фаз как
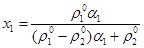 ,
,  (2.11)
(2.11)
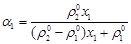 ,
,  (2.12)
(2.12)
Уравнение импульсов. Будем полагать, что двухфазную систему в целом можно рассмотреть как идеальную среду с введением для нее еще одного параметра, а именно давления 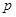 . Это допущение означает, что тензор напряжений является чисто шаровым и его компоненты можно записать в виде
. Это допущение означает, что тензор напряжений является чисто шаровым и его компоненты можно записать в виде

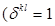 ,
, 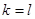 ;
; 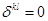 ,
,  (2.13)
(2.13)
где 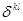 - символ Кронекера. Тогда уравнение импульсов для всей смеси в целом запишется в виде
- символ Кронекера. Тогда уравнение импульсов для всей смеси в целом запишется в виде
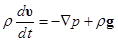 (2.14)
(2.14)
 (k=1,2,3) (2.15)
(k=1,2,3) (2.15)
Здесь  - удельномассовая сила.
- удельномассовая сила.
В том случае, когда течение потенциальное, массовые силы потенциальные, а смесь в целом можно считать баротропной средой  , уравнение импульсов (2.14) сводится к интегралу Коши-Лагранжа
, уравнение импульсов (2.14) сводится к интегралу Коши-Лагранжа
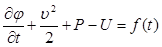 (2.16)
(2.16)
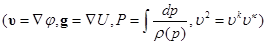
Уравнение неразрывности (2.2) при этом можно привести к виду
 (2.17)
(2.17)
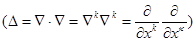
Введенный здесь параметр 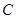 , как известно, выражает скорость звука в среде. Таким образом, система уравнений для равновесной по скоростям двухфазной системы, в рамках вышепринятых допущениях сводится к двум уравнениям из (2.16.) и (2.17). При этом основная проблема сводится к построению уравнения состояния вида
, как известно, выражает скорость звука в среде. Таким образом, система уравнений для равновесной по скоростям двухфазной системы, в рамках вышепринятых допущениях сводится к двум уравнениям из (2.16.) и (2.17). При этом основная проблема сводится к построению уравнения состояния вида 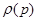 или
или  с учетом специфики конкретных двухфазных систем.
с учетом специфики конкретных двухфазных систем.
ЗАКЛЮЧЕНИЕ
В данной курсовой работе мы провели теоретическое исследование зависимости фазовой скорости и коэффициента затухания от частоты в смеси воды с воздушными включениями при значениях объемного содержания газовой фазы αg0 =10-3 и 10-4. Провели сравнительный дисперсионный анализ двух пузырьковых жидкостей с различными несущими фазами. Пришли к выводу, что скорость звука в водовоздушной и спиртовоздушной смесях распространяется одинаково и стремится к скорости звука в чистой жидкости. Что касается коэффициентов затухания, то они практически совпадают.
СПИСОК ЛИТЕРАТУРЫ
1. Нигматулин Р.И. Динамика многофазных сред. М.: Наука, 1987.
2. Накоряков В.Е., Покусаев Б.Г., Шрейбер И.Р. Волновая динамика газо- и парожидкостных сред. М.: Энергоатомиздат, 1990. 248 с.
3. Нигматуллин Р. И., Шагапов В. Ш., Вахитова Н. К. Проявление сжимаемости несущей фазы при распространении волн в пузырьковой среде ДАН СССР. 1989. Т. 304. № 35. С. 1077-1081.
4. Лепендин Л.Ф. Акустика. М.: Высшая школа, 1978.
5. Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей. М.: Наука, 1972.
6. Сарапулова В.В. Особенности преломления и отражения звука на границе раздела между водой и пузырьковой жидкостью // Вестник КемГУ. Вып. 2 (58). Т.2. 2014.
МОДЕЛИ ГЕТЕРОГЕННЫХ СИСТЕМ
ОСНОВНЫЕ ПОНЯТИЯ И МЕТОДЫ ГИДРОДИНАМИКИ ДИСПЕРСНЫХ СИСТЕМ
В окрестности точки, определяемой радиусом вектором  берем частицу с объемом
берем частицу с объемом 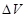 и с общей массой
и с общей массой 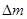 , при этом полагаем, что
, при этом полагаем, что
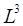 >>
>>  >>
>>  >>
>> 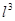
где 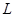 характерный линейный разрез задачи,
характерный линейный разрез задачи, 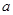 и
и 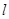 -линейные размеры дисперсных частиц и среднее расстояние между соседними частицами.
-линейные размеры дисперсных частиц и среднее расстояние между соседними частицами.
Для дисперсной системы, состоящей из двух составляющих, можно записать
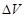 =
= 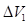 +
+  и
и 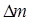 =
= 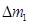 +
+ 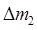 (1.1)
(1.1)
где  и
и 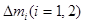 части объема и массы в
части объема и массы в 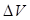 , приходящиеся к
, приходящиеся к
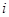 -ой фазе. Введем следующие параметры [1]
-ой фазе. Введем следующие параметры [1]
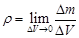 ,
, 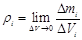 ,
,  (1.2)
(1.2)
 ,
, 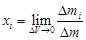 ,
, 
Здесь 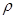 - средняя плотность смеси в целом и
- средняя плотность смеси в целом и  ,
, 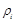 - средние и истинные плотности фаз,
- средние и истинные плотности фаз, 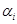 и
и 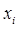 - объемные и массовые содержания (или концентрации) фаз. Очевидно, что из определения этих параметров следует зависимость между ними в виде, используя [1]
- объемные и массовые содержания (или концентрации) фаз. Очевидно, что из определения этих параметров следует зависимость между ними в виде, используя [1]
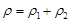 ,
,  ,
, 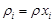 (1.3)
(1.3)
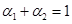 ,
, 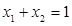
Кроме того, на основе первого соотношения из (1.1) с учетом (1.2) нетрудно получить
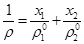 (1.4)
(1.4)
Пусть 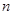 и
и 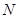 - число дисперсных частиц в единице объема массы дисперсной системы, тогда между этими параметрами имеется следующая связь
- число дисперсных частиц в единице объема массы дисперсной системы, тогда между этими параметрами имеется следующая связь
 (1.5)
(1.5)
Для дальнейшего примем, что дисперсная фаза представляет собой сферические частицы одинакового радиуса  . Тогда имеет место кинематическая связь [1]
. Тогда имеет место кинематическая связь [1]
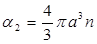 (1.6)
(1.6)
ОДНОСКОРОСТНАЯ МОДЕЛЬ
Уравнения неразрывности. Примем, что составляющие смеси движутся с одинаковыми скоростями (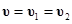 ). Это означает, что в изучаемой проблеме скольжение фаз несущественно. Например, рассматриваются медленные процессы, когда характерные времена задачи
). Это означает, что в изучаемой проблеме скольжение фаз несущественно. Например, рассматриваются медленные процессы, когда характерные времена задачи 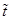 значительно превышают времена релаксации скоростей неравновесности
значительно превышают времена релаксации скоростей неравновесности 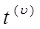 для двухфазной смеси
для двухфазной смеси 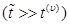 . По аналогии с обычными однофазными системами в этом случае должно иметь место следующее уравнение сохранения массы для всей смеси в целом [1]
. По аналогии с обычными однофазными системами в этом случае должно иметь место следующее уравнение сохранения массы для всей смеси в целом [1]
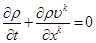 или
или 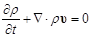 (2.1)
(2.1)
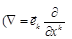 ,
, 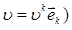
Эти уравнения можно записать, используя
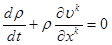 или
или 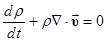 (2.2)
(2.2)
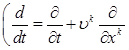 или
или 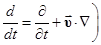

Пусть, в общем случае, может происходить массообмен между составляющими двухфазной системы. Такая ситуация может иметь место, например, в парокапельной смеси. Пар может конденсироваться, или, наоборот, капельки могут испаряться. Введем параметры 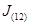 и
и 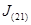 , описывающие интенсивность перехода массы из первой фазы во вторую и, наоборот, из второй фазы в первую. Эти параметры отнесены к единице объема смеси. Тогда для каждой составляющей двухфазной системы можем записать следующие уравнения, выражающие закон сохранения масс [1]
, описывающие интенсивность перехода массы из первой фазы во вторую и, наоборот, из второй фазы в первую. Эти параметры отнесены к единице объема смеси. Тогда для каждой составляющей двухфазной системы можем записать следующие уравнения, выражающие закон сохранения масс [1]
 (2.3)
(2.3)
и
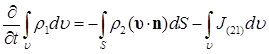
Используя теорему Гаусса-Остроградского, из (2.3) можем получить уравнение неразрывности в форме Эйлера [1]
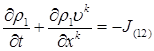 и
и 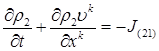 (2.4)
(2.4)
Складывая эти уравнения, получаем уравнение неразрывности (2.1) для всей смеси в целом. При этом необходимо отметить, что введенные параметры для описания межфазного массообмена должны удовлетворять условию

Следовательно, достаточно задавать один из этих параметров  (или
(или 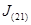 ). Для определенности в последующем примем обозначения
). Для определенности в последующем примем обозначения 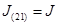 тогда
тогда
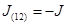 . В случае отсутствия массообмена между фазами имеет место
. В случае отсутствия массообмена между фазами имеет место 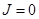 .
.
Запишем уравнение импульсов для первой фазы 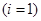 в терминал истинная плотность - объемная концентрация при
в терминал истинная плотность - объемная концентрация при 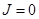 как
как
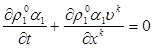 (2.5)
(2.5)
Если это составляющее несжимаемое 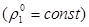 , отсюда следует
, отсюда следует
 (2.6)
(2.6)
В том случае, когда вторая фаза также несжимаема, то аналогично с (2.6) будем иметь
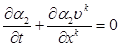 (2.7)
(2.7)
Складывая уравнения (2.6) и (2.7) с учетом 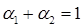 получим
получим
 (2.8)
(2.8)
Таким образом, в случае, когда обе фазы несжимаемые, уравнение неразрывности сводится для поля скоростей к обычному виду для несжимаемой однофазной среды.
Подставляя в уравнение неразрывности среднюю плотность в виде 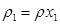 и учитывая уравнение неразрывности для всей смеси в целом (2.1) можем получить:
и учитывая уравнение неразрывности для всей смеси в целом (2.1) можем получить:
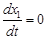 или
или 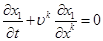 (2.9)
(2.9)
Если предположить, что при течении дисперсной системы не происходит образование и исчезновение дисперсных частиц (отсутствуют процессы дробления или слипания частиц, например), то аналогично с уравнениям неразрывности фаз, можно записать уравнение сохранения числа дисперсных частиц
 (2.10)
(2.10)
Подставляя сюда выражение 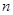 из (1.5) с учетом уравнения неразрывности всей смеси (2.1) получим:
из (1.5) с учетом уравнения неразрывности всей смеси (2.1) получим:
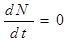 или
или  (2.10)
(2.10)
На основе кинематических зависимостей (1.3) нетрудно получить формулы, связывающие массовые и объемные концентрации фаз как
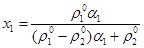 ,
,  (2.11)
(2.11)
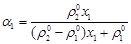 ,
,  (2.12)
(2.12)
Уравнение импульсов. Будем полагать, что двухфазную систему в целом можно рассмотреть как идеальную среду с введением для нее еще одного параметра, а именно давления 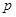 . Это допущение означает, что тензор напряжений является чисто шаровым и его компоненты можно записать в виде
. Это допущение означает, что тензор напряжений является чисто шаровым и его компоненты можно записать в виде

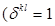 ,
, 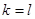 ;
; 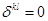 ,
,  (2.13)
(2.13)
где 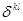 - символ Кронекера. Тогда уравнение импульсов для всей смеси в целом запишется в виде
- символ Кронекера. Тогда уравнение импульсов для всей смеси в целом запишется в виде
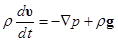 (2.14)
(2.14)
 (k=1,2,3) (2.15)
(k=1,2,3) (2.15)
Здесь  - удельномассовая сила.
- удельномассовая сила.
В том случае, когда течение потенциальное, массовые силы потенциальные, а смесь в целом можно считать баротропной средой  , уравнение импульсов (2.14) сводится к интегралу Коши-Лагранжа
, уравнение импульсов (2.14) сводится к интегралу Коши-Лагранжа
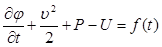 (2.16)
(2.16)
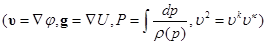
Уравнение неразрывности (2.2) при этом можно привести к виду
 (2.17)
(2.17)
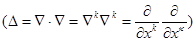
Введенный здесь параметр 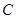 , как известно, выражает скорость звука в среде. Таким образом, система уравнений для равновесной по скоростям двухфазной системы, в рамках вышепринятых допущениях сводится к двум уравнениям из (2.16.) и (2.17). При этом основная проблема сводится к построению уравнения состояния вида
, как известно, выражает скорость звука в среде. Таким образом, система уравнений для равновесной по скоростям двухфазной системы, в рамках вышепринятых допущениях сводится к двум уравнениям из (2.16.) и (2.17). При этом основная проблема сводится к построению уравнения состояния вида 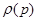 или
или  с учетом специфики конкретных двухфазных систем.
с учетом специфики конкретных двухфазных систем.
УРАВНЕНИЕ СОСТОЯНИЯ ДЛЯ РАВНОВЕСНОЙ ПО СКОРОСТЯМ ГАЗОЖИДКОСТНОЙ СИСТЕМЫ
Вместо индексов (1) и (2), соответствующих первой и второй фазам для газожидкостной смеси будем использовать соответственно нижние индексы 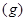 и
и 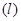 . Пусть фазовые переходы отсутствуют
. Пусть фазовые переходы отсутствуют 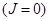 . Для дальнейшего обозначим
. Для дальнейшего обозначим 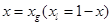 ,
, 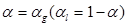 . Тогда из уравнения неразрывности следует (2.9), которое запишется как
. Тогда из уравнения неразрывности следует (2.9), которое запишется как
 или
или  (3.1)
(3.1)
Выражения (1.4) для средней плотности имеет вид
 (3.2)
(3.2)
Будем полагать, что в процессе движения жидкость ведет себя как акустически сжимаемая среда, а поведение газа политропическое. Тогда можем записать
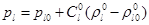 и
и 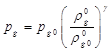 (3.3)
(3.3)
Здесь 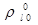 и
и 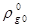 - значения плотности, соответствующие значениям давления
- значения плотности, соответствующие значениям давления 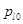 и
и 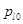 ;
; 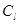 - величины скорости звука для жидкостной фазы, γ- показатель политропы. В частности, если поведение газа изотермическое, то γ=1, а если адиабатическое, то величина γ равна показателю адиабаты для данного газа.
- величины скорости звука для жидкостной фазы, γ- показатель политропы. В частности, если поведение газа изотермическое, то γ=1, а если адиабатическое, то величина γ равна показателю адиабаты для данного газа.
В дальнейшем будем считать, что давление в фазах равны 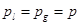 и, кроме того, вместо
и, кроме того, вместо 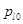 и
и  примем одно и тоже значение давления
примем одно и тоже значение давления 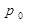
 . Вместо
. Вместо 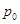 обычно будем использовать значение давления для некоторого исходного равновесного состояния. Подставляя значение
обычно будем использовать значение давления для некоторого исходного равновесного состояния. Подставляя значение  ,
, 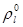 из (3.3) в (3.2) получим
из (3.3) в (3.2) получим
 (3.4)
(3.4)
Таким образом, получим уравнение состояния вида
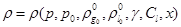
В этом уравнении, величины 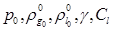 , определяющие исходное состояние системы и свойства составляющих (газа и жидкости), входят как некоторые постоянные параметры. Что касается величины массового содержания газа
, определяющие исходное состояние системы и свойства составляющих (газа и жидкости), входят как некоторые постоянные параметры. Что касается величины массового содержания газа 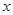 , то для каждой лагранжевой частицы оно будет постоянным параметром. При эйлеровом описании, в общем случае массовое газосодержание
, то для каждой лагранжевой частицы оно будет постоянным параметром. При эйлеровом описании, в общем случае массовое газосодержание 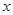 зависит как от времени, так и от пространственных координат
зависит как от времени, так и от пространственных координат 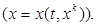 Однако, если для некоторого состояния оно (например, при
Однако, если для некоторого состояния оно (например, при  - однородно
- однородно  , то массовое газосодержание будет постоянным и по времени и по координате. В дальнейшем будем рассматривать именно такие ситуации. Тогда в (3.5) х также будет постоянный параметр. В этом случае при течении такой смеси величина плотности будет определяться значением давления и, следовательно, газожидкостная смесь в целом будет баротропной средой.
, то массовое газосодержание будет постоянным и по времени и по координате. В дальнейшем будем рассматривать именно такие ситуации. Тогда в (3.5) х также будет постоянный параметр. В этом случае при течении такой смеси величина плотности будет определяться значением давления и, следовательно, газожидкостная смесь в целом будет баротропной средой.
Определим скорость звука для такой среды.
Для этого продифференцируем левую и правую части уравнения (3.4) по давлению 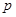 . Тогда будем иметь
. Тогда будем иметь
 ,
, 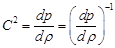 (3.5)
(3.5)
Это уравнение можно записать как
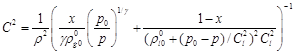 (3.6)
(3.6)
Формула (3.6) совместно с (3.4) дает зависимость величины скорости звука от текущего давления  .
.
Как уже отмечено, если для исходного равновесного состояния газожидкостная смесь однородна, то в (3.6) имеет место 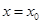 , где
, где 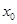 - значение массового содержания газа для исходного состояния. В этом случае на основании (2.11) можем записать:
- значение массового содержания газа для исходного состояния. В этом случае на основании (2.11) можем записать:
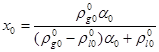 (3.7)
(3.7)
Подставляя это выражение для 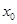 вместо
вместо 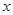 в (3.4) и (3.6), получим уравнение состояния и формулу для скорости звука, в которых в качестве параметра, ответственного за состав смеси, фигурирует начальное объемное газосодержание
в (3.4) и (3.6), получим уравнение состояния и формулу для скорости звука, в которых в качестве параметра, ответственного за состав смеси, фигурирует начальное объемное газосодержание 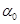 . Определим скорость звука для исходного состояния. Подставляя в формулу (3.6)
. Определим скорость звука для исходного состояния. Подставляя в формулу (3.6)  , получим
, получим
 (3.8)
(3.8)
Отсюда при  и
и  соответственно получим выражение для скорости звука для «чистых» газа и жидкости
соответственно получим выражение для скорости звука для «чистых» газа и жидкости
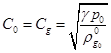 и
и  (3.9)
(3.9)
Проанализируем формулу (3.8) для случая, когда массовое газосодержание мало  . Из формулы (3.7), учитывая при этом, что в большинстве случаев имеет место
. Из формулы (3.7), учитывая при этом, что в большинстве случаев имеет место 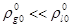 , получим
, получим
 (3.10)
(3.10)
Отсюда видно, что это условие 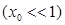 выполняется для объемных содержаний газовой фазы, удовлетворяющих условию
выполняется для объемных содержаний газовой фазы, удовлетворяющих условию
 (3.11)
(3.11)
Для водовоздушной смеси при нормальных условиях, например, имеет место  , поэтому неравенство (3.11) выполняется и при объемных содержаниях газа
, поэтому неравенство (3.11) выполняется и при объемных содержаниях газа 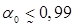 .
.
В этом случае, с учетом 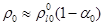 , из (3.8) получим следующую формулу для скорости звука
, из (3.8) получим следующую формулу для скорости звука
 (3.12)
(3.12)
Из этой формулы следует, что вклад сжимаемости жидкости, определяемый вторым слагаемым в подкоренном выражении (3.12), растет с уменьшением объемного содержания газа 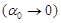 .
.
Проанализируем эту формулу для пузырьковой жидкости ( ). Пренебрегая
). Пренебрегая 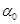 по сравнению с единицей из (3.12) получим
по сравнению с единицей из (3.12) получим
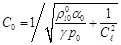 (3.13)
(3.13)
Отсюда получим, что сжимаемость жидкости в плане определения скорости звука скажется при
 (3.14)
(3.14)
Для водовоздушной смеси при нормальных условиях  имеем
имеем 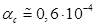 . Следовательно, сжимаемость жидкости проявляется лишь при очень низких объемных содержаниях газа.
. Следовательно, сжимаемость жидкости проявляется лишь при очень низких объемных содержаниях газа.
Пренебрегая сжимаемостью жидкости (формально полагая в (3.12)  ), для скорости звука получим формулу Мэллока
), для скорости звука получим формулу Мэллока
 (3.15)
(3.15)
Из этой формулы нетрудно видеть, что минимальная величина скорости звука достигается при  . Для этой скорости из (3.15) следует
. Для этой скорости из (3.15) следует
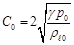 (3.16)
(3.16)
Для водовоздушной смеси при нормальных условиях отсюда имеем 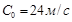 .
.



 берем частицу с объемом
берем частицу с объемом 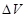 и с общей массой
и с общей массой 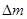 , при этом полагаем, что
, при этом полагаем, что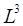 >>
>>  >>
>>  >>
>> 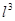
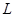 характерный линейный разрез задачи,
характерный линейный разрез задачи, 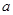 и
и 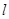 -линейные размеры дисперсных частиц и среднее расстояние между соседними частицами.
-линейные размеры дисперсных частиц и среднее расстояние между соседними частицами.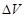 =
= 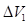 +
+  и
и 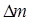 =
= 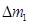 +
+ 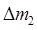 (1.1)
(1.1) и
и 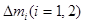 части объема и массы в
части объема и массы в 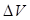 , приходящиеся к
, приходящиеся к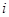 -ой фазе. Введем следующие параметры [1]
-ой фазе. Введем следующие параметры [1]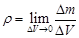 ,
, 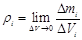 ,
,  (1.2)
(1.2) ,
, 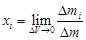 ,
, 
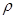 - средняя плотность смеси в целом и
- средняя плотность смеси в целом и  ,
, 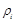 - средние и истинные плотности фаз,
- средние и истинные плотности фаз, 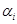 и
и 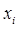 - объемные и массовые содержания (или концентрации) фаз. Очевидно, что из определения этих параметров следует зависимость между ними в виде, используя [1]
- объемные и массовые содержания (или концентрации) фаз. Очевидно, что из определения этих параметров следует зависимость между ними в виде, используя [1]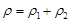 ,
,  ,
, 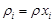 (1.3)
(1.3)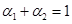 ,
, 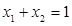
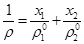 (1.4)
(1.4)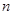 и
и 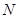 - число дисперсных частиц в единице объема массы дисперсной системы, тогда между этими параметрами имеется следующая связь
- число дисперсных частиц в единице объема массы дисперсной системы, тогда между этими параметрами имеется следующая связь (1.5)
(1.5) . Тогда имеет место кинематическая связь [1]
. Тогда имеет место кинематическая связь [1]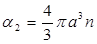 (1.6)
(1.6)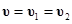 ). Это означает, что в изучаемой проблеме скольжение фаз несущественно. Например, рассматриваются медленные процессы, когда характерные времена задачи
). Это означает, что в изучаемой проблеме скольжение фаз несущественно. Например, рассматриваются медленные процессы, когда характерные времена задачи 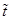 значительно превышают времена релаксации скоростей неравновесности
значительно превышают времена релаксации скоростей неравновесности 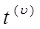 для двухфазной смеси
для двухфазной смеси 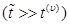 . По аналогии с обычными однофазными системами в этом случае должно иметь место следующее уравнение сохранения массы для всей смеси в целом [1]
. По аналогии с обычными однофазными системами в этом случае должно иметь место следующее уравнение сохранения массы для всей смеси в целом [1]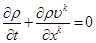 или
или 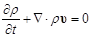 (2.1)
(2.1)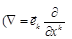 ,
, 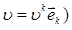
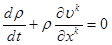 или
или 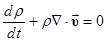 (2.2)
(2.2)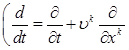 или
или 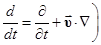

 и
и  , описывающие интенсивность перехода массы из первой фазы во вторую и, наоборот, из второй фазы в первую. Эти параметры отнесены к единице объема смеси. Тогда для каждой составляющей двухфазной системы можем записать следующие уравнения, выражающие закон сохранения масс [1]
, описывающие интенсивность перехода массы из первой фазы во вторую и, наоборот, из второй фазы в первую. Эти параметры отнесены к единице объема смеси. Тогда для каждой составляющей двухфазной системы можем записать следующие уравнения, выражающие закон сохранения масс [1] (2.3)
(2.3)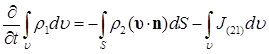
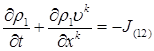 и
и 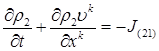 (2.4)
(2.4)
 (или
(или 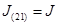 тогда
тогда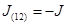 . В случае отсутствия массообмена между фазами имеет место
. В случае отсутствия массообмена между фазами имеет место 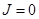 .
.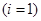 в терминал истинная плотность - объемная концентрация при
в терминал истинная плотность - объемная концентрация при 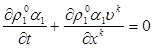 (2.5)
(2.5)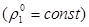 , отсюда следует
, отсюда следует (2.6)
(2.6)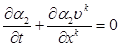 (2.7)
(2.7)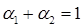 получим
получим (2.8)
(2.8)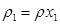 и учитывая уравнение неразрывности для всей смеси в целом (2.1) можем получить:
и учитывая уравнение неразрывности для всей смеси в целом (2.1) можем получить: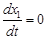 или
или 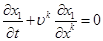 (2.9)
(2.9) (2.10)
(2.10)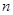 из (1.5) с учетом уравнения неразрывности всей смеси (2.1) получим:
из (1.5) с учетом уравнения неразрывности всей смеси (2.1) получим: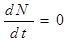 или
или  (2.10)
(2.10)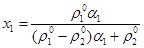 ,
,  (2.11)
(2.11)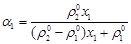 ,
,  (2.12)
(2.12)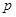 . Это допущение означает, что тензор напряжений является чисто шаровым и его компоненты можно записать в виде
. Это допущение означает, что тензор напряжений является чисто шаровым и его компоненты можно записать в виде
 ,
, 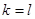 ;
; 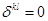 ,
,  (2.13)
(2.13)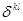 - символ Кронекера. Тогда уравнение импульсов для всей смеси в целом запишется в виде
- символ Кронекера. Тогда уравнение импульсов для всей смеси в целом запишется в виде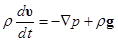 (2.14)
(2.14) (k=1,2,3) (2.15)
(k=1,2,3) (2.15) - удельномассовая сила.
- удельномассовая сила. , уравнение импульсов (2.14) сводится к интегралу Коши-Лагранжа
, уравнение импульсов (2.14) сводится к интегралу Коши-Лагранжа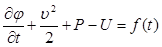 (2.16)
(2.16)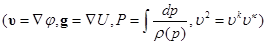
 (2.17)
(2.17)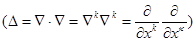
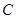 , как известно, выражает скорость звука в среде. Таким образом, система уравнений для равновесной по скоростям двухфазной системы, в рамках вышепринятых допущениях сводится к двум уравнениям из (2.16.) и (2.17). При этом основная проблема сводится к построению уравнения состояния вида
, как известно, выражает скорость звука в среде. Таким образом, система уравнений для равновесной по скоростям двухфазной системы, в рамках вышепринятых допущениях сводится к двум уравнениям из (2.16.) и (2.17). При этом основная проблема сводится к построению уравнения состояния вида 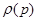 или
или  с учетом специфики конкретных двухфазных систем.
с учетом специфики конкретных двухфазных систем.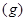 и
и 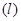 . Пусть фазовые переходы отсутствуют
. Пусть фазовые переходы отсутствуют 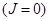 . Для дальнейшего обозначим
. Для дальнейшего обозначим 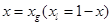 ,
, 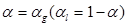 . Тогда из уравнения неразрывности следует (2.9), которое запишется как
. Тогда из уравнения неразрывности следует (2.9), которое запишется как или
или  (3.1)
(3.1) (3.2)
(3.2)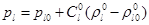 и
и 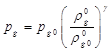 (3.3)
(3.3)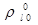 и
и 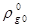 - значения плотности, соответствующие значениям давления
- значения плотности, соответствующие значениям давления 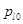 и
и 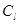 - величины скорости звука для жидкостной фазы, γ- показатель политропы. В частности, если поведение газа изотермическое, то γ=1, а если адиабатическое, то величина γ равна показателю адиабаты для данного газа.
- величины скорости звука для жидкостной фазы, γ- показатель политропы. В частности, если поведение газа изотермическое, то γ=1, а если адиабатическое, то величина γ равна показателю адиабаты для данного газа.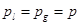 и, кроме того, вместо
и, кроме того, вместо  примем одно и тоже значение давления
примем одно и тоже значение давления 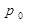
 . Вместо
. Вместо 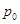 обычно будем использовать значение давления для некоторого исходного равновесного состояния. Подставляя значение
обычно будем использовать значение давления для некоторого исходного равновесного состояния. Подставляя значение  ,
, 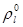 из (3.3) в (3.2) получим
из (3.3) в (3.2) получим (3.4)
(3.4)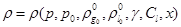
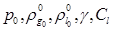 , определяющие исходное состояние системы и свойства составляющих (газа и жидкости), входят как некоторые постоянные параметры. Что касается величины массового содержания газа
, определяющие исходное состояние системы и свойства составляющих (газа и жидкости), входят как некоторые постоянные параметры. Что касается величины массового содержания газа 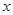 , то для каждой лагранжевой частицы оно будет постоянным параметром. При эйлеровом описании, в общем случае массовое газосодержание
, то для каждой лагранжевой частицы оно будет постоянным параметром. При эйлеровом описании, в общем случае массовое газосодержание 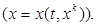 Однако, если для некоторого состояния оно (например, при
Однако, если для некоторого состояния оно (например, при  - однородно
- однородно  , то массовое газосодержание будет постоянным и по времени и по координате. В дальнейшем будем рассматривать именно такие ситуации. Тогда в (3.5) х также будет постоянный параметр. В этом случае при течении такой смеси величина плотности будет определяться значением давления и, следовательно, газожидкостная смесь в целом будет баротропной средой.
, то массовое газосодержание будет постоянным и по времени и по координате. В дальнейшем будем рассматривать именно такие ситуации. Тогда в (3.5) х также будет постоянный параметр. В этом случае при течении такой смеси величина плотности будет определяться значением давления и, следовательно, газожидкостная смесь в целом будет баротропной средой.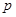 . Тогда будем иметь
. Тогда будем иметь ,
, 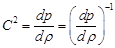 (3.5)
(3.5)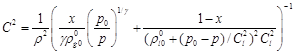 (3.6)
(3.6) .
.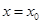 , где
, где 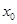 - значение массового содержания газа для исходного состояния. В этом случае на основании (2.11) можем записать:
- значение массового содержания газа для исходного состояния. В этом случае на основании (2.11) можем записать: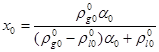 (3.7)
(3.7)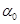 . Определим скорость звука для исходного состояния. Подставляя в формулу (3.6)
. Определим скорость звука для исходного состояния. Подставляя в формулу (3.6)  , получим
, получим (3.8)
(3.8) и
и  соответственно получим выражение для скорости звука для «чистых» газа и жидкости
соответственно получим выражение для скорости звука для «чистых» газа и жидкости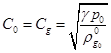 и
и  (3.9)
(3.9) . Из формулы (3.7), учитывая при этом, что в большинстве случаев имеет место
. Из формулы (3.7), учитывая при этом, что в большинстве случаев имеет место 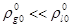 , получим
, получим (3.10)
(3.10)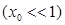 выполняется для объемных содержаний газовой фазы, удовлетворяющих условию
выполняется для объемных содержаний газовой фазы, удовлетворяющих условию (3.11)
(3.11) , поэтому неравенство (3.11) выполняется и при объемных содержаниях газа
, поэтому неравенство (3.11) выполняется и при объемных содержаниях газа 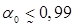 .
.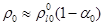 , из (3.8) получим следующую формулу для скорости звука
, из (3.8) получим следующую формулу для скорости звука (3.12)
(3.12)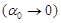 .
. ). Пренебрегая
). Пренебрегая 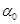 по сравнению с единицей из (3.12) получим
по сравнению с единицей из (3.12) получим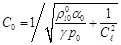 (3.13)
(3.13) (3.14)
(3.14) имеем
имеем 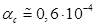 . Следовательно, сжимаемость жидкости проявляется лишь при очень низких объемных содержаниях газа.
. Следовательно, сжимаемость жидкости проявляется лишь при очень низких объемных содержаниях газа. ), для скорости звука получим формулу Мэллока
), для скорости звука получим формулу Мэллока (3.15)
(3.15) . Для этой скорости из (3.15) следует
. Для этой скорости из (3.15) следует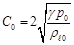 (3.16)
(3.16)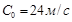 .
.


