Теорема 1. Пусть H - поле характеристики p ¹ 0. Тогда для любого числа k Î N и для любых элементов a, b Î H справедливы свойства:

Доказательство. 1)Докажем первое утверждение теоремы методом математической индукции по k. Пусть k = 1. Тогда имеем
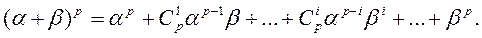 (3)
(3)
Так как p - простое число, то при 0< i < p биноминальный коэффициент
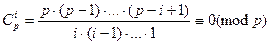 .
.
Поэтому при всех таких i
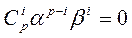 .
.
Таким образом, из (3) получаем, что
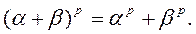
Предположим, что формула 1 верна при k и докажем ее для k + 1. По доказанному выше и по индуктивному предположению выводим:
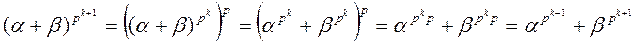 .
.
2) Так как для четного числа p для любого элемента b Î H имеем 2×b = 0, b + b = 0, -b = b, то получаем 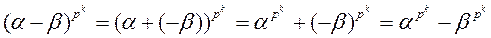 .
.
Свойства 3 и 4 следуют из определения поля.ÿ
Теорема 2. Пусть p – простое число, n – натуральное число, q = pn. Тогда поле разложения H над полем Z p многочлена f (x) = xq – x есть конечное поле из q элементов.
Доказательство. Все корни многочлена f (x)лежат в поле H. Рассмотрим множество F всех корней многочлена f (x). Если a, b - корни многочлена f (x), то
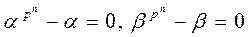 , т.е.
, т.е. 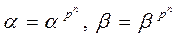 .
.
Тогда по теореме 1

Следовательно, для любых элементов из F их сумма, разность, произведение, частное, если знаменатель не равен нулю, принадлежит F. Тогда F – подполе поля H, содержащее все корни многочлена f (x). В силу минимальности поля разложения получаем H = F. ÿ
Теорема 3. Для любого простого числа p и для любого натурального числа n существует конечное поле, содержащее q = pn элементов.
Доказательство. В силу теоремы 2 таким полем является поле разложения многочлена f (x) = xq – x. ÿ
Порядок элемента конечного поля и его свойства
Пусть (Fq *, +) – мультипликативная группа конечного поля Fq. Так как порядок этой группы равен q -1, то для любого элемента a Î Fq * имеем равенство
aq - 1= 1. (1)
Определение 1. Порядком элемента a Î Fq * называется наименьшее натуральное число d, для которого выполняется условие
a d= 1. (2)
Порядок элемента обозначается через ord a.
Теорема 1. Для любого элемента a Î Fq * выполняются свойства:
1) порядок ord a существует и ord a £ q – 1;
2) ord a делит q – 1;
3) для любого натурального числа n
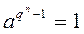 .
.
4) для любого натурального числа n и для любого элемента a Î Fq
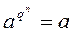 .
.
Доказательство.
1) Следует из равенства (1).
2) Следует из того, что порядок элемента конечной группы является делителем порядка группы.
3) Следует из того, что q – 1 делит qn – 1.
4) Для a = 0 очевидно, а для a ¹0 следует из 3).ÿ
Теорема 2. Для любого элемента a Î Fq * порядка d выполняются свойства:
10 для любых натуральных чисел a m = a k тогда и только тогда, когда m º k (mod d);
20 все элементы множества
1, a, a 2, …, a d-1 (3)
различны;
30 элементы множества (3) есть все корни многочлена
x d - 1; (4)
40 для любого натурального числа k порядок элемента ak равен 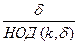 .
.
50 для любого натурального числа k ord ak = d тогда и только тогда, когда числа k и d взаимно простые;
60 число элементов b Î Fq порядка d равно j(d).
Доказательство. Свойства 10 и 20 следуют из свойства порядка элемента мультипликативной группы.
30 Так как для любого натурального числа k
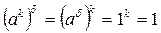 ,
,
то все элементы множества (3) являются корнями многочлена (4). Так как многочлен степени d над полем Fq имеет не более d корней, то все корни многочлена (4) исчерпываются элементами множества (3).
40 Пусть ord ak = m. Тогда
 .
.
Тогда по следствию теоремы Лагранжа d делит km. Поэтому
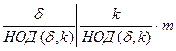 .
.
Так как числа
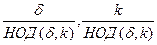
взаимно простые, то
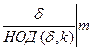 . (5)
. (5)
С другой стороны,
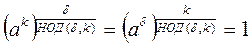 .
.
Поэтому
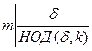 . (6)
. (6)
Из (5) и (6) следует, что
 . (7)
. (7)
50 Пусть числа k иd взаимно простые. Тогда НОД(k, d) = 1 и из формулы (7) следует, что ord ak = d. Обратно, если ord ak = d, то из формулы (7) следует, что НОД(k, d) = 1 и числа k иd взаимно простые.
60 По определению всяких элемент b порядка d корень уравнения (4). По свойству 30 все корни уравнения (4) исчерпываются элементами множества (3). По свойству 50 элемент ak из множества (3) имеет порядок k тогда и только тогда, когда (k, d) = 1. Таким образом, элементов порядка d в поле Fq столько, сколько во множестве {0, 1, …, d -1} имеется чисел взаимно простых с числом d. По определению функции Эйлера таких чисел j(d). Следовательно, в поле Fq имеется j(d) элементов, имеющих порядок d.ÿ




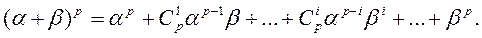 (3)
(3)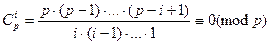 .
.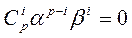 .
.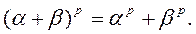
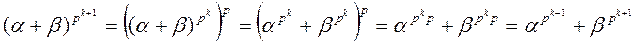 .
.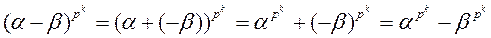 .
.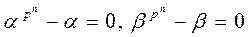 , т.е.
, т.е. 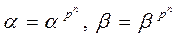 .
.
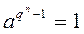 .
.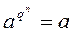 .
.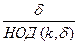 .
.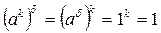 ,
, .
.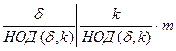 .
.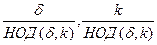
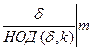 . (5)
. (5)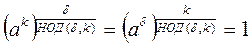 .
.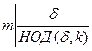 . (6)
. (6) . (7)
. (7)


