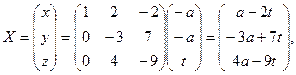Определение 1. Непрерывной или цепной дробью называется выражение вида:
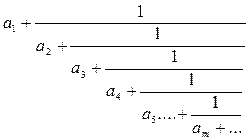
Числа a 1, a 2, a 3,… - целые и называются членами цепной дроби; ai > 0, i =2,3,… Если число членов цепной дроби конечно и равно m, то цепная дробь называется конечно цепной дробью длины m, если число членов цепной дроби бесконечное, то дробь называется бесконечной цепной дробью. Цепную дробь обозначают в виде:
[ a 1, a 2, a 3,…, am, …].
Любая конечная цепная дробь

есть рациональное число. Обратно, любое рациональное число изображается цепной дробью. Пусть a / b рациональное число, представимое в виде несократимой дроби. Применим, числам a, b алгоритм Евклида и получим систему равенств вида:
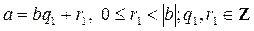 ,
,
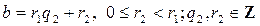 ,
,
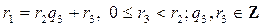 ,
,
…
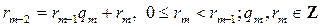 ,
,
где rm = НОД(a, b) = 1. Из этих равенств последовательно получим:
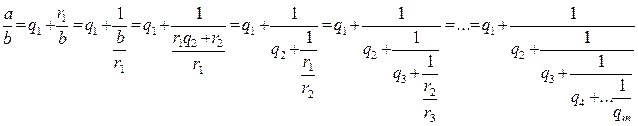
Теорема 1. Любое рациональное число a / b представляется в виде конечной цепной дроби, членами которой являются неполные частные, полученные в алгоритме Евклида, примененном к числам a, b. ÿ
Пример 1. Представить число a / b, a = 2346, b = 1456 в виде цепной дроби. Применяя вычисления примера 1 из параграфа 4, получаем:
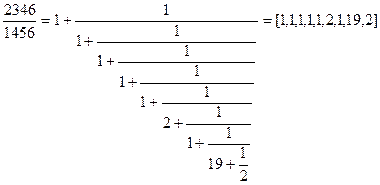 .
.
Таким образом, НОД(a, b) = 2.
Определение 2. Несократимая рациональная дробь 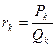 , равная конечной цепной дроби
, равная конечной цепной дроби
 ,
,
записанной для конечной цепной дроби [ a 1, a 2, a 3,…, am ], k =1,2,…, m, или для бесконечной цепной дроби [ a 1, a 2, a 3,…, am, …], k =1,2,…, m,… называется k -й подходящей добью к данной цепной дроби.
Определение 3. Бесконечная цепная дробь [ a 1, a 2, a 3,…, am, …], называется сходящейся, если существует предел последовательности ее подходящих дробей { rk } и этот предел 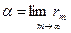 называется значением бесконечно цепной дроби. Также говорят, что действительное число a представляется данной цепной дробью.
называется значением бесконечно цепной дроби. Также говорят, что действительное число a представляется данной цепной дробью.
Теорема 2. Любая бесконечная цепная дробь сходится. Обратно любое действительное число a представляется в виде конечной или бесконечной цепной дроби.
Члены цепной дроби последовательно вычисляются по следующему алгоритму:
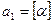 ,
,
Если a 1 = a, то процесс закончен, если 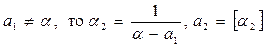 .
.
Если a 2 = a 1, то процесс закончен, если 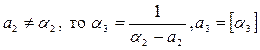 .
.
Таким образом, на k -м мы имеем
Если ak -1 = a k -1, то процесс закончен, если 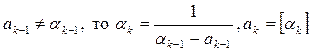 .
.
Пример 2. Представить число 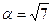 в виде цепной дроби.
в виде цепной дроби.
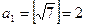 ,
,
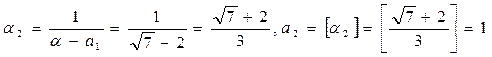 ,
,
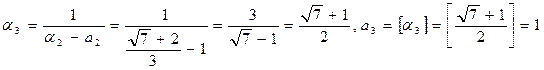 ,
,
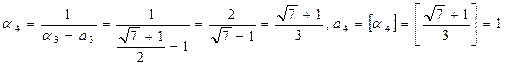 ,
,
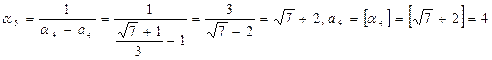 .
.
Дальше a i и ai начинают повторяться. Поэтому имеем
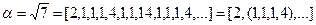 .
.
Бесконечная цепная дробь, у которой последовательность неполных частных, начиная с некоторого места начинает повторяться называется периодической. В примере 2 была получена периодическая цепная дробь.
Найдем формулу для числителей и знаменателей подходящих дробей:
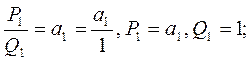
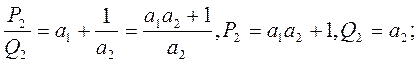
Теорема 3. Числители и знаменатели k -подходящей дроби (k >1) вычисляются по формулам:
Pk = Pk- 1 ak + Pk- 2, Qk = Qk- 1 ak + Qk- 2, (1)
где полагается
P 0 = 1, Q 0 = 0, P 1 = a 1, Q 1 = 1. (2)
Доказательство. Формулы (1) и (2) справедливы при k =1, 2. Допустим, что формулы (1) справедливы для k и докажем их для k + 1. По индуктивному предположению
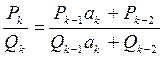 .
.
Так как k + 1-я подходящая дробь получается из k -й подходящей дроби, заменой числа ak на 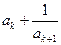 , то получаем:
, то получаем:
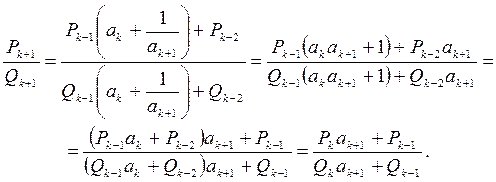
Отсюда следует утверждение теоремы.
Пример 3. Вычислить все числители и знаменатели цепной дроби, полученной в примере 1. 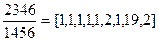 . Вычисления проводим по формулам (1), (2), записывая результаты вычислений в таблицу.
. Вычисления проводим по формулам (1), (2), записывая результаты вычислений в таблицу.
| k
| 0
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
|
| ak
| -
| 1
| 1
| 1
| 1
| 1
| 2
| 1
| 19
| 2
|
| Pk
| 1
| 1
| 2
| 3
| 5
| 8
| 21
| 29
| 572
| 1173
|
| Qk
| 0
| 1
| 1
| 2
| 3
| 5
| 13
| 18
| 355
| 728
|
Заметим, что последняя подходящая дробь совпадает с данным рациональным числом.
Подходящие дроби обладают следующими свойствами, которые легко доказываются методом математической индукции по формулам теоремы 3.
10 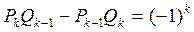 .
.
20 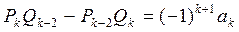 .
.
30 Последовательность знаменателей строго возрастает с номера k =2: 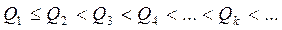 .
.
40 Числители и знаменатели подходящих дробей взаимно простые числа.
50 Каждая подходящая дробь с четным номером больше любой подходящей дроби с нечетным номером.
60 Последовательность подходящих дробей с четными номерами убывает.
70 Последовательность подходящих дробей с нечетными номерами возрастает.
80 Если несократимая рациональная дробь a / b представляется цепной дробью длины m, то 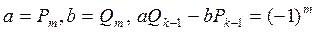 .
.
Определение 4. Линейным диофантовым или неопределенным уравнением называется уравнение вида:
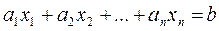 , (3)
, (3)
где a 1, a 2, a 3,…, an, b – известные целые числа, и решение уравнения ищется в целых числах.
Теорема 4. Линейное диофантово уравнение (3) разрешимо тогда и только тогда, когда оно число d = НОД (a 1, a 2, a 3,…, an) делит число b.
Доказательство. Необходимость следует из определения НОД и свойств делимости целых чисел. Достаточность следует из теоремы 2 параграфа 4.ÿ
Теорема 5. Пусть a, b, c Î Z, a ¹ 0 или b ¹ 0, d = НОД(a, b). Если (x 0, y 0) решение уравнения
ax + b y = c, (4)
Тогда все решения уравнения (2.3) находятся по формулам:
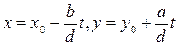 , (5)
, (5)
где t - произвольное целое число. Решение (x 0, y 0) можно найти по формулам
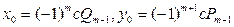 , (6)
, (6)
где m – длина цепной дроби при разложении числа a / b в цепную дробь, Pm - 1, Qm - 1 – числители и знаменатели соответствующих дробей.
Доказательство. Пусть (x ¢, y ¢) произвольное решение уравнения (2.4). Тогда справедливо равенство a x ¢ + b y ¢ = c. Так как решение уравнения (2.4), то справедливо равенство a x 0 + b y 0 = c. Почленно, вычитая из первого равенства второе, получим: a (x ¢ - x 0) + b (y ¢ - y 0 ) = c. Разделим обе части этого равенства на d получим
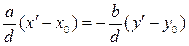 .
.
Так как 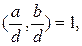 то отсюда получим
то отсюда получим 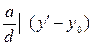 . Поэтому
. Поэтому 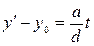 , где t Î Z.
, где t Î Z.
Отсюда 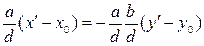 , и
, и 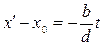 . Таким образом, решение уравнения (4) находится по формуле (5).
. Таким образом, решение уравнения (4) находится по формуле (5).
Обратно, легко проверить, что любые числа (x, y), найденные по формуле (5) являются решения уравнения (4).
Частное решение (x 0, y 0) уравнения (4) находится, методом разложения числа a / b в цепную дробь. Вычисляются все подходящие дроби и применяется свойство 80.
Примеры 4. Решить ДУ 2346 x - 1456 y = 22.
Так как НОД(2346, 1456) = 2 и 2|22, то данное уравнение разрешимо и равносильно уравнению 1173 x - 728 y = 11. Разлагаем дробь 1173/728 в цепную дробь 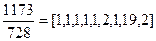 и находим длину дроби m = 9, и все ее подходящие дроби (см. пример 4). Находим P 8 = 572, Q 8 = 355,
и находим длину дроби m = 9, и все ее подходящие дроби (см. пример 4). Находим P 8 = 572, Q 8 = 355,
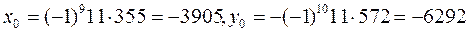 .
.
Тогда общее решение уравнения имеет вид:
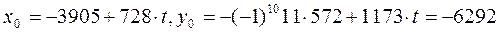 .
.
Уравнение (3) в частных случаях легко решить методом замены переменных.
Пример 5. Метод замены переменных решить уравнение 34 x - 13 y = 53.
Так как 34 = 13×2 + 8, то уравнение представим в виде
(13×2 + 8) x - 13 y = 53, 8 x + 13(2 x - y) = 53.
Отсюда, полагая z =2 x - y, получим уравнение 8 x + 13 z = 53. Продолжая такие замены переменных, последовательно находим
13 = 8×1+ 5, 8 x + (8×1 + 5) z = 53, 8(x + z) - 5 z = 53, w = x + z, 8 w + 5 z = 53; 8 = 5×1 + 3, (5×1 + 3) w + 5 z = 53, 3 w + 5(w + z)= 53, u = w + z, 3 w + 5 u = 53;
5 = 3×1 + 2, 3 w + (3×1 + 2) u = 53, 3(w + u)+ 2 u = 53, v = w + u, 3 v + 2 u = 53;
3 = 2×1 + 1, (2×1 + 1) v + 2 u = 53, v + 2(v + u)= 53, t = v + u, v + 2 t = 53.
Из полученных равенств последовательно находим
v = 53 - 2 t,
u = t - v = t - (53 - 2 t) = 3 t -53,
w = v - u = 53 - 2 t - (3 t -53) = 106 - 5 t,
z = u - w = 3 t -53- (106 - 5 t) = 8 t -159,
x = w - z = 106 - 5 t - (8 t -159) = 265 - 13 t,
y =2 x - z = 2(265 - 13 t) - (8 t -159) = 689 - 34 t.
Алгоритм решения ЛДУ ax + by = c, b ¹ 0.
Ввод: коэффициенты a, b уравнения и свободный член c.
m:=0; r:= b;a 1:= a;;b 1:= b;
{вычисление НОД чисел a, b и проверка условия разрешимости уравнения}
while r ¹0 do m:= m + 1;(qm, r): = div (a 1, b 1); a 1: =b 1; b 1: =r; end while;
(c 1, r): = div (c, b 1);
if r =0 then
a 1:= a /с; b 1:= b;
{вычисление подходящих дробей}
P 0:= 1; Q 0:= 0; P 1:= q 1; Q 1:= 1;
if m >1 then for i:=2… m; Pi: = Pi- 1 qi + Pi- 2; Qi: = Qi- 1 qi + Qi- 2; end for; end if;
{вывод решения}
x (t): = (-1) mc 1 Qm -1 - b 1 t; y (t): = (-1) m+ 1 c 1 Pm -1 + a 1 t;
else s:=« нет решений»;
Вывод: s и x (t), y (t).
Замечание. Можно вычислять знаменатели цепной дроби, числители Pm -1 и знаменатели Qm -1 в одном цикле, не используя массивы.
Определение 5. Системой m линейных диофантовых уравнений с n неизвестными x 1, x 2,…, xn (СЛДУ) называется система уравнений вида:
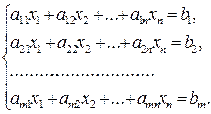 (7)
(7)
где a 11, a 12,..., amn - фиксированные целые числа (рациональные или целые алгебраические), называемые коэффициентами при неизвестных, b 1, b 2,..., bm - фиксированные целые числа, называемые свободными членами.
Если все свободные члены в системе линейных уравнений равны нулю, то система линейных уравнений называется однородной.
Определение 6. Решением системы диофантовых линейных уравнений (7) называется такой упорядоченный набор n целых чисел чисел 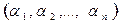 , при подстановке которых в каждое из уравнений системы (2.1) вместо соответственно неизвестных x1, x2,..., xn каждое из уравнений системы превращается в истинное числовое равенство.
, при подстановке которых в каждое из уравнений системы (2.1) вместо соответственно неизвестных x1, x2,..., xn каждое из уравнений системы превращается в истинное числовое равенство.
Теорема 6. Пусть A - целая матрица размерности m ´ n, 1£ k £.min{ m, n }. При целочисленных элементарных преобразованиях матрицы A НОД миноров k -го порядка матрицы не изменяется.
Определение 7. Целая матрица D = (dij) размерности m ´ n называется матрицей канонического вида, если она обладает свойствами:
1) все элементы dij = 0 для любых i = 1, 2,…, m; j = 1, 2,…, n; i ¹ j;
2) все элементы dij ³ 0 для любых i = 1, 2,…, k, где k = min { m. n };
3) dii | di+ 1, i+ 1 для любых i = 1, 2,…, k- 1, где k = min { m, n }.
Элементы dij, i = 1, 2,…, k, где k = min { m, n }, называем диагональными элементами канонической матрицы. Обозначим число ненулевых диагональных элементов канонической матрицы через r. Очевидно, что r = rang D.
Теорема 7. Любую целую матрицу конечным числом элементарных преобразований строк и столбцов можно привести к матрице канонического вида, при этом r = rang A.
Диагональные элементы d 11,…, drr, r = rang A, матрицы канонического вида, эквивалентной матрице A, называются элементарными делителями матрицы A.
Теорема 8. Система ЛДУ (2.1) разрешима тогда и только тогда, когда элементарные делители матрицы A и расширенной матрицы 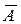 СЛДУ соответственно равны.
СЛДУ соответственно равны.
Пример 6. Выяснить разрешимость данной СЛДУ
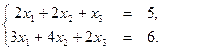
Решение. Приводим матрицу и расширенную матрицу СЛДУ к каноническому виду.
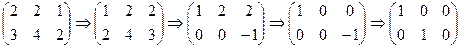 ,
,
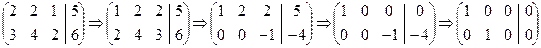
Так как элементарные делители матриц равны, то данная СЛДУ разрешима.
Алгоритм решения СЛДУ Пусть дана СЛДУ (2.1). Запишем ее в матричном виде:
AX = B, (9)
Расширенную матрицу СЛДУ (8) расширим вторично, приписав к ней снизу единичную матрицу размерности n ´ n и нулевую матрицу размерности n ´1. Получим дважды расширенную матрицу СЛДУ:
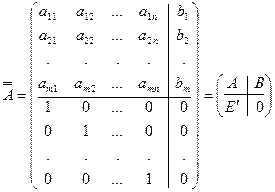 .
.
Преобразуем матрицу A к каноническому виду D, выполняя элементарные преобразования над первыми m строками и первыми столбцами n матрицы 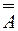 . Тогда матрица B перейдет в матрицу F = U 1 B, где U 1 - произведение элементарных матриц, соответствующих элементарным преобразованиям строк. Единичная матрица E ¢ перейдет в матрицу U 2, где U 2 - произведение элементарных матриц, соответствующих элементарным преобразованиям столбцов. Получим матрицу:
. Тогда матрица B перейдет в матрицу F = U 1 B, где U 1 - произведение элементарных матриц, соответствующих элементарным преобразованиям строк. Единичная матрица E ¢ перейдет в матрицу U 2, где U 2 - произведение элементарных матриц, соответствующих элементарным преобразованиям столбцов. Получим матрицу:
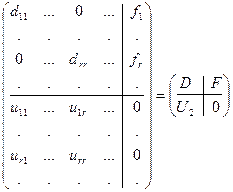 .
.
Полученной матрице соответствует матричное уравнение:
DY = F, (10)
где Y = U 2-1 X, F = U 1 B, которому соответствует СЛДУ
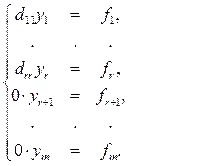 (11)
(11)
Если хотя бы один из элементов fr + 1,…, fm не равен нулю, или хотя бы один из элементов fk не делится на число dkk (k =1, 2, …, r), то система (11), а поэтому и система (8) не имеют решений. Если же
d 11| f 1,…, drr | fr, fr + 1 = 0,…, fm = 0,
то разделим 1-е, 2-е, …, r -е уравнения системы (11) соответственно на числа d 11, d 22, …, drr находим y 1, y 2, …, yr. Значения неизвестных yr +1,…, yn можно брать произвольным образом: yr +1= t 1, …, yn = tn - r. Следовательно, находим:
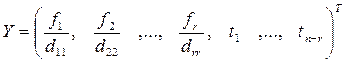 .
.
Так как Y = U 2-1 X, то отсюда находим
X = U 2 Y, (12)
и оно зависит от n - r свободных переменных t 1, …, tn - r Î Z.
Пример 7. Решить диофантово уравнение:
4 x 1 + 17 x 2 + 31 x 3 - 21 x 4 = 17.
Решение. Составим дважды расширенную матрицу и приведем ее к каноническому виду:
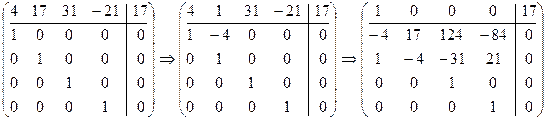
Отсюда находим
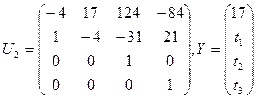 ,
,
t 1, t 2, t 3 - свободные неизвестные. Тогда
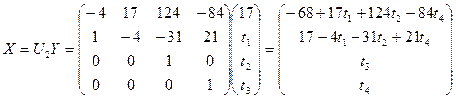 .
.
Отсюда
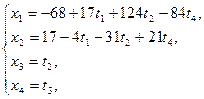 , где t 1, t 2, t 3 Î Z.
, где t 1, t 2, t 3 Î Z.
Пример 8. Решить СЛДУ:
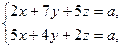
где a - произвольный целый параметр.
Решение. Составим дважды расширенную матрицу и приведем ее к каноническому виду:
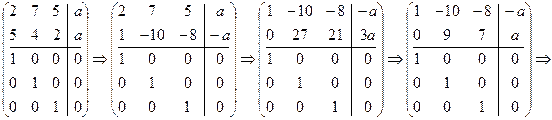
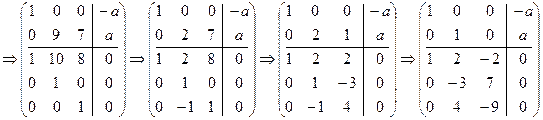 .
.
Отсюда
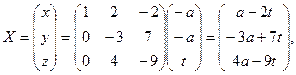
где. Следовательно, x = a - 2 t, y = -3 a + 7 t, z = 4 a - 9 t, где t Î Z.



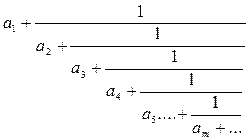

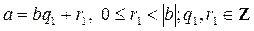 ,
,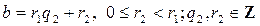 ,
,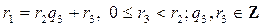 ,
,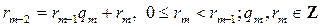 ,
,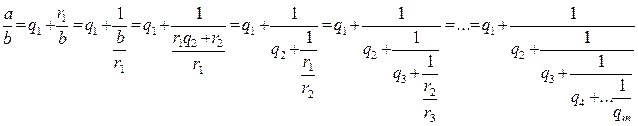
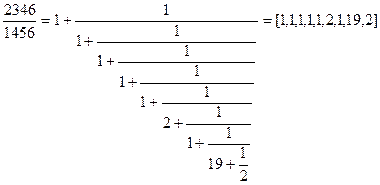 .
.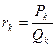 , равная конечной цепной дроби
, равная конечной цепной дроби ,
,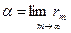 называется значением бесконечно цепной дроби. Также говорят, что действительное число a представляется данной цепной дробью.
называется значением бесконечно цепной дроби. Также говорят, что действительное число a представляется данной цепной дробью.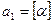 ,
,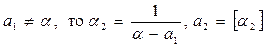 .
.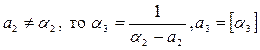 .
.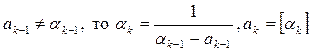 .
.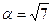 в виде цепной дроби.
в виде цепной дроби.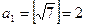 ,
,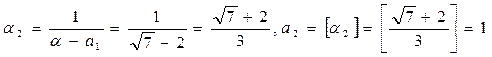 ,
,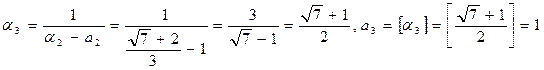 ,
,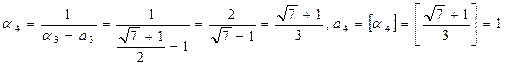 ,
,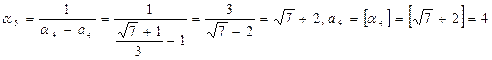 .
.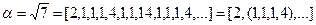 .
.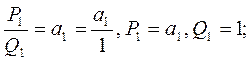
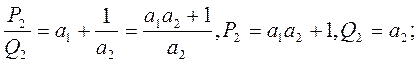
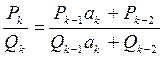 .
.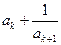 , то получаем:
, то получаем: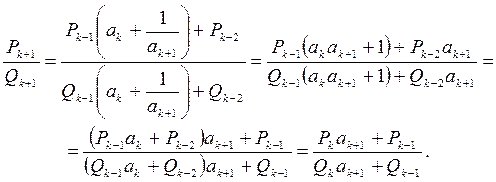
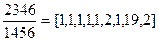 . Вычисления проводим по формулам (1), (2), записывая результаты вычислений в таблицу.
. Вычисления проводим по формулам (1), (2), записывая результаты вычислений в таблицу.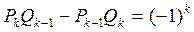 .
.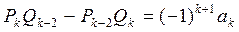 .
.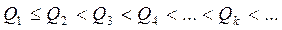 .
.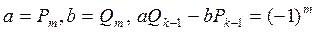 .
.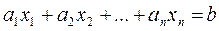 , (3)
, (3)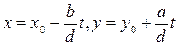 , (5)
, (5)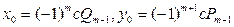 , (6)
, (6)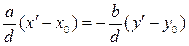 .
.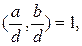 то отсюда получим
то отсюда получим 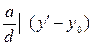 . Поэтому
. Поэтому 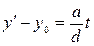 , где t Î Z.
, где t Î Z.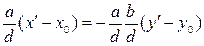 , и
, и 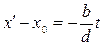 . Таким образом, решение уравнения (4) находится по формуле (5).
. Таким образом, решение уравнения (4) находится по формуле (5).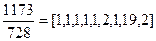 и находим длину дроби m = 9, и все ее подходящие дроби (см. пример 4). Находим P 8 = 572, Q 8 = 355,
и находим длину дроби m = 9, и все ее подходящие дроби (см. пример 4). Находим P 8 = 572, Q 8 = 355,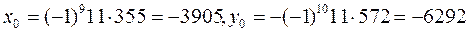 .
.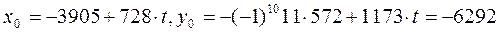 .
.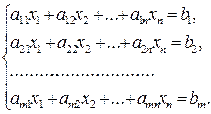 (7)
(7)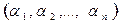 , при подстановке которых в каждое из уравнений системы (2.1) вместо соответственно неизвестных x1, x2,..., xn каждое из уравнений системы превращается в истинное числовое равенство.
, при подстановке которых в каждое из уравнений системы (2.1) вместо соответственно неизвестных x1, x2,..., xn каждое из уравнений системы превращается в истинное числовое равенство.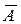 СЛДУ соответственно равны.
СЛДУ соответственно равны. 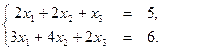
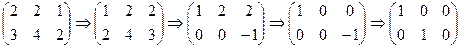 ,
,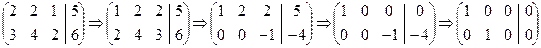
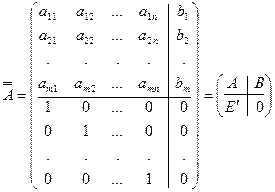 .
. . Тогда матрица B перейдет в матрицу F = U 1 B, где U 1 - произведение элементарных матриц, соответствующих элементарным преобразованиям строк. Единичная матрица E ¢ перейдет в матрицу U 2, где U 2 - произведение элементарных матриц, соответствующих элементарным преобразованиям столбцов. Получим матрицу:
. Тогда матрица B перейдет в матрицу F = U 1 B, где U 1 - произведение элементарных матриц, соответствующих элементарным преобразованиям строк. Единичная матрица E ¢ перейдет в матрицу U 2, где U 2 - произведение элементарных матриц, соответствующих элементарным преобразованиям столбцов. Получим матрицу: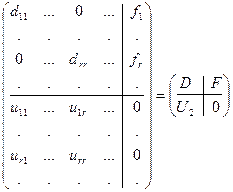 .
.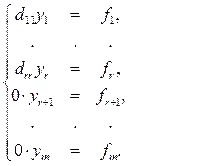 (11)
(11)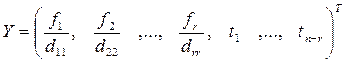 .
.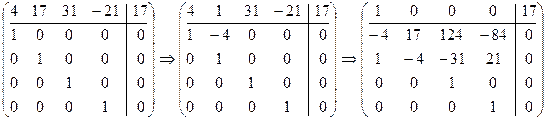
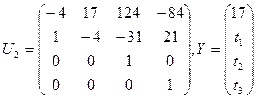 ,
,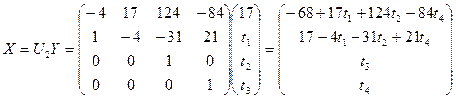 .
.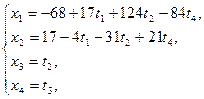 , где t 1, t 2, t 3 Î Z.
, где t 1, t 2, t 3 Î Z.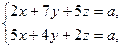
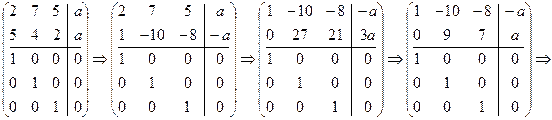
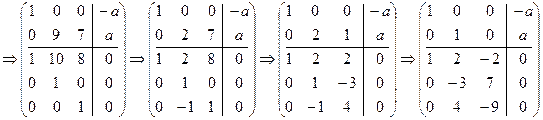 .
.