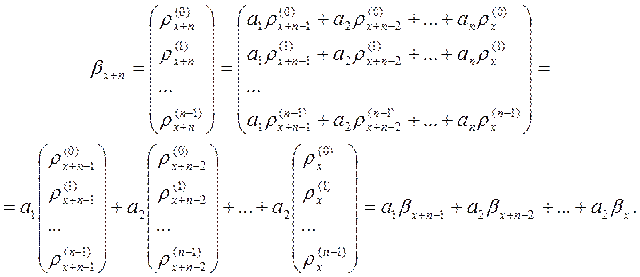Пусть
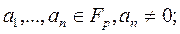
d x + n = a 1d x+n- 1+…+ an+ 1d n +1 + an d n; (1)
f (l) = l n - a 1l n - 1 - …+ an Î Fp [l] –
Пусть Vn – n -мерное векторное пространство над полем Fp; 0 – нулевой вектор пространства, a·b - скалярное произведение векторов a и b Î Vn; c - характер аддитивной группы поля 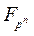 ; c0 – главный характер аддитивной группы поля
; c0 – главный характер аддитивной группы поля 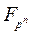 .
.
Для каждого j Î {0, 1,…, n -1} 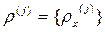 - решение уравнения (1) с начальными значениями:
- решение уравнения (1) с начальными значениями:
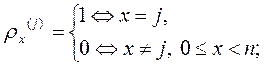
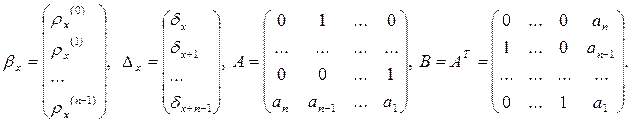 ,
,
где A – матрица рекурсивного уравнения (1); B – матрица, транспонированная к матрице A. Имеем
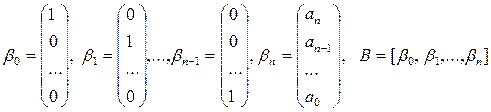 .
.
Пусть d( j ) , 0 £ j £ k – все различные решения уравнения (1), такие что ни одно из них не может быть получено сдвигом из другого; их множество условимся обозначать символом L (f), таким образом, L (f) = {d( j ) | 0 £ j £ k }. Пусть
tj = t(d( j ));
 . (2)
. (2)
Теорема 1. Множество векторов
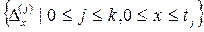 (3)
(3)
совпадает с множеством всех векторов пространства Vn.
Доказательство. Так как (3) Í Vn, то достаточно показать, что любой вектор a = (a0, a1, …, a n - 1) Î Vn принадлежит (3). Вектор a можно взять в качестве начального значения решения уравнения (1) и по нему построить решение уравнения (1). Так как среди начальных значений (2) содержаться все возможные, отличные друг от друга с точностью до сдвига, то вектор a содержится среди векторов (3).
Теорема 2. Справедливы равенства
a) " x Î Z A ·D x = D x + 1;
b) " x Î Z Ax ·D0 = D x .
Доказательство. a)
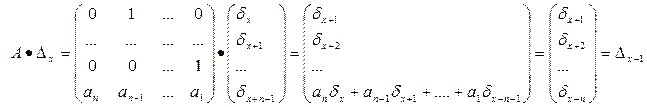 .
.
b) Из a) последовательно получаем
Ax ·D0 = Ax- 1·(A ·D0) = Ax- 1·D1 = …= A ·D x- 1 = D x.
Теорема 3. " x Î Z," y Î Z
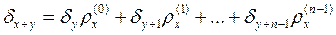 . (4)
. (4)
Доказательство. При фиксированном y равенство (4) верно при x = 0, x = 1, …, x = n -1:
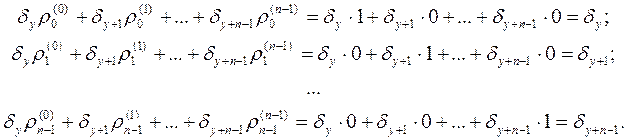
Далее
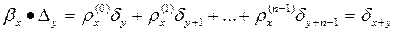 .
.
Таким образом, решения d x + y и b x ·D y равны при n последовательных значениях переменного x. Следовательно, они равны при любых x Î Z.
Теорема 4. Справедливы равенства
c) " x Î Z B ·b x = b x + 1;
d) " x Î Z Bx ·b0 = b x .
Доказательство. a) В равенстве (4) полагаем y = 1, заменяем d x на r x ( k ) и получим
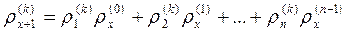 . (5)
. (5)
В равенстве (5) полагаем последовательно k = 0, k = 1, …, k = n -1:
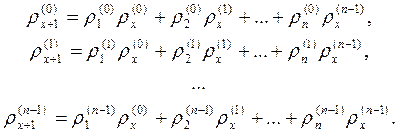
Таким образом, получаем
b x + 1 = B ·b x
и равенство a) доказано.
b) Из a) последовательно получаем
Bx ·b0 = Bx- 1·(B ·b0) = Bx- 1·b1 = …= B ·b x- 1 = b x.
Теорема 5. " x Î Z
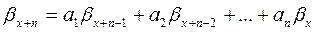 . (6)
. (6)
Доказательство. Из равенства (1) имеем
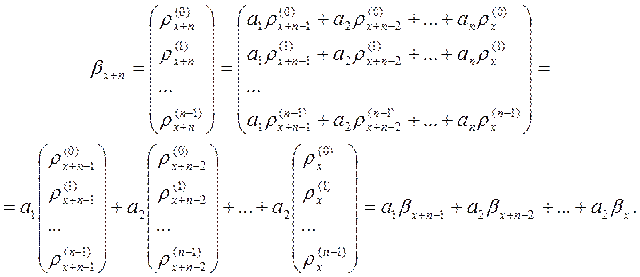
Теорема 6. Справедливы утверждения:
a) Если d - главное решение уравнения (1), то для любого x Î Z векторы D x, D x + 1, …, D x + n - 1 линейно независимы над полем Fp.
b) для любого x Î Z векторы b x, b x + 1, …, b x + n - 1 линейно независимы над полем Fp.
Доказательство. a) Докажем, что векторы D x, D x + 1, …, D x + n - 1линейно независимы над полем Fp. Допустим противное, что существуют не все равные нулю элементы c 1, c 2, …, cn поля Fp, что
c 1D x + c 2D x + 1 + …+ cn D x + n - 1 = 0. (7)
Умножая обе части этого равенства на A - x, по теореме 2 получим
c 1D0 + c 2D1 + …+ cn D n - 1 = 0.
Последнее невозможно, так как при изоморфном отображении t пространства S (f) на Vn базису (d, T ·d, …, Tn - 1·d) отвечает набор (D0, D1, …,D n - 1). При изоморфизме линейно независимая система векторов переходит в линейно независимую систему.
b) Допустим противное, что существуют не все равные нулю элементы c 1, c 2, …, cn поля Fp, что
c 1b x + c 2b x + 1 + …+ cn b x + n - 1 = 0. (7)
Умножая обе части этого равенства на B - x, по теореме 5 получим
c 1b0 + c 2b1 + …+ cn b n - 1 = 0.
Последнее невозможно, так как векторы (b0, b1, …,b n - 1) линейно независимы над полем Fp.
Теорема 7. t(b) = t.
Доказательство. Так как примитивный период главного решения уравнения (1) равен t, а главное решение базис пространства S (f), то
" x Î Z [d x + t = d x ]
для любого решения d уравнения (1). Следовательно,
" x Î Z [b x + t = b x ].
С другой стороны, если
" x Î Z [b x + m = b x ],
то
" x Î Z [r x + m ( j ) = r x ( j )]
для каждого j = 0,…, n - 1 и в частности для j = n – 1. А так как r( n - 1) – главное решение уравнения (1), то m ³ t.



 ; c0 – главный характер аддитивной группы поля
; c0 – главный характер аддитивной группы поля  .
.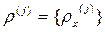 - решение уравнения (1) с начальными значениями:
- решение уравнения (1) с начальными значениями: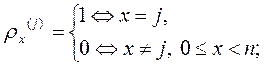
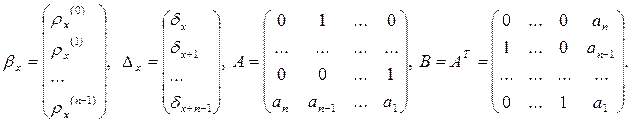 ,
,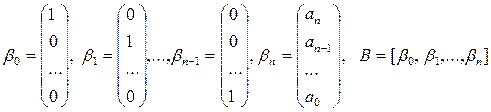 .
. . (2)
. (2)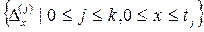 (3)
(3)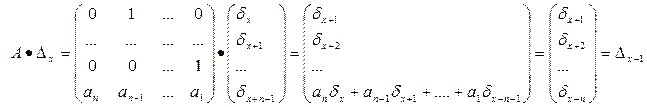 .
.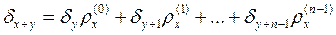 . (4)
. (4)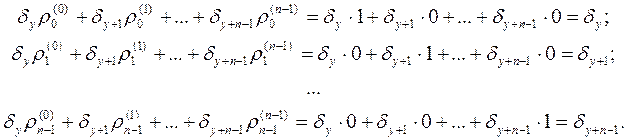
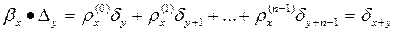 .
.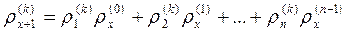 . (5)
. (5)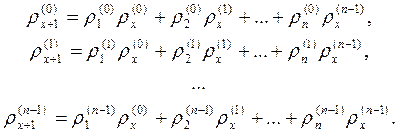
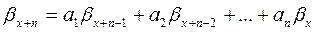 . (6)
. (6)