440305
ПАМ
Толстиков А.В.
Лекция 10. Последовательности над конечными полями
1. Псевдослучайные последовательности и их применение в криптграфии..
2. Алгебра последовательностей над конечным полем.
3. Линейные рекуррентные последовательности над конечным полем.
4. Периодичность ЛРП. Длина периода ЛРП. Максимальные ЛРП.
5. Аннулирующие многочлены.
6. Вычисление длины периода ЛРП.
7. Регистр сдвига.
8. Число появлений наборов фиксированных знаков на полном периоде линейной рекуррентной последовательности.
9. Свойства решений линейного рекуррентного уравнения
10. Характеры групп и суммы характеров.
11. Максимальные линейные рекуррентные последовательности как псевдослучайные последовательности.
Литература. Нечаев В.И. – С. 49-60, 69-78, 85-87.
Глухов М.М. и др. -Т. 2. – С. 292-361.
Периодичность ЛРП. Длина периода ЛРП.
Максимальные ЛРП.
Определение 1. Последовательность d = {d x } Î s называется периодической, если существует такое неотрицательное число k, и такое натуральное числоt, что для всех x Î N 0, x ³ k выполняется равенство d x + t = d x.
Наименьшие натуральные числа k и t, удовлетворяющие условиям определения 1 называются соответственно, периодом и длиной предпериода последовательности d.
Периодическую последовательность можно изобразить графически следующим образом:
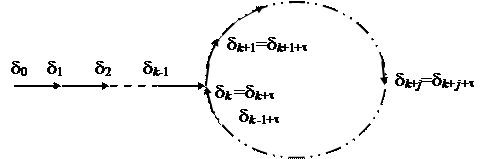
Условие периодичности последовательности эквивалентно условию
Tk + t·d = Tk ·d, Tk + t·d - Tk ·d = 0,
или
l k (l t -1)·d = 0. (1)
Обозначим через k (d) и t(d) соответственно длину предпериода и периода последовательности d.
Теорема 1. Пусть d - периодическая последовательность элементов поля F и k Î N 0, t Î N. Тогда условие
для всех x Î N 0, x ³ k равенство d x + t = d x (2)
равносильно условию
k ³ k (d), t(d)| t. (3)
Доказательство. Пусть k 0= k (d), t 0= t(d).Тогда в силу сказанного выше k 0Î N 0, t 0 Î N, наименьшие натуральные числа, удовлетворяющие условию (1).
Пусть теперь для чисел k Î N 0, t Î N выполняется условие (2), тогда выполняется и условие (1). НОД многочленов l k (l t -1)·d, 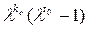 . Применяя теорему о вычислении НОД многочленов методом получим
. Применяя теорему о вычислении НОД многочленов методом получим
 ,
,
где k 1 = min(k 0, k), t 1 = НОД(t 0, t). Так как 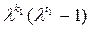 - линейная комбинация многочленов l k (l t -1)·d,
- линейная комбинация многочленов l k (l t -1)·d, 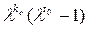 , то следует, что равенство (1) выполняется для чисел k = k 1, t = t 1. Тогда k 1 ³ t 0 или t 1 ³ t 0. Из этих неравенств следует, что k 1 = t 0 и t 1 = t 0.. Тогда k ³ k 0, t 0| t.
, то следует, что равенство (1) выполняется для чисел k = k 1, t = t 1. Тогда k 1 ³ t 0 или t 1 ³ t 0. Из этих неравенств следует, что k 1 = t 0 и t 1 = t 0.. Тогда k ³ k 0, t 0| t.
Обратно, пусть выполняются условия (3). Тогда
 .
.
Поэтому для чисел k и t выполняется условие (1). Отсюда выполняется условие (2).
Следствие 1. Если d - периодическая последовательность над полем F, то для любого многочлена g (l) Î F [l] последовательность a = g (l)·d – периодическая над полем F, причем
k (a) £ k (d),t(a)|t(d). (4)
Доказательство. Пусть k 0= k (d), t 0= t(d). Тогда
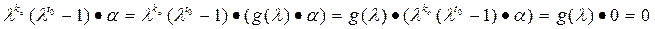 .
.
Тогда по теореме 1 k (a) £ k 0,t(a)| t 0.
Следствие 2. Если a, b - периодические последовательности над полем F, то последовательность d = a + b периодическая и
k (d) £ max{ k (a), k (b)),t(d)|НОК(t(a),t(b)). (5)
При этом:
1) если k (a) ¹ k (b), то
k (d) = max{ k (a), k (b)); (6)
2) если (t(a),t(b)) = 1, то
t(d) = НОК(t(a),t(b)); (7)
3) если a, b - ЛРП, для которых можно указать взаимно простые характеристические многочлены, то справедливы равенства (6), (7).
Доказательство. Пусть k = max{ k (a), k (b)), t = НОК(t(a),t(b)). Тогда по теореме 1  Следовательно,
Следовательно,
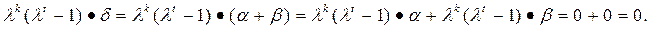
k 0= k (d), t 0= t(d). Тогда по теореме 11, получаем соотношения (4).
1) Пусть k (a) ¹ k (b), например, k (a) < k (b). Тогда k = k (b). По доказанному выше k (d) £ k. Докажем, что k (d) £ k. Допустим противное, что k (d) < k. Тогда многочлен 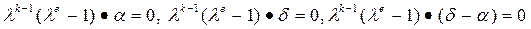 . Поэтому
. Поэтому 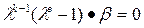 и по теореме 1 k (b)£ k – 1. Что невозможно. Следовательно, k (d) = k и формула (5) доказана.
и по теореме 1 k (b)£ k – 1. Что невозможно. Следовательно, k (d) = k и формула (5) доказана.
2) Пусть (t(a),t(b)) = 1, и t(d) = t. Далее
 .
.
Так как t |(tl), t |t(a), то по теореме 1 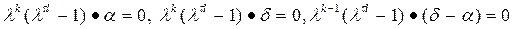 .
.
Поэтому  и по теореме 1 t (b) | t l. Так как (t (b), l) = 1, то t (b) | t. Аналогично доказывает.
и по теореме 1 t (b) | t l. Так как (t (b), l) = 1, то t (b) | t. Аналогично доказывает.
3) Пусть a, b - ЛРП, для которых можно указать взаимно простые характеристические многочлены f (l), g (l). Тогда f (l)·a= 0, g (l)·b= 0 и поэтому (f (l) g (l))·(a+b) = 0. Так как 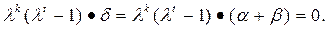
Тогда по теореме 1 k (a) £ k 0,t(a)| t 0.
разложения на неприводимые множители
Теорема 1. Любое решение d = {d x }Î s (f) линейного рекуррентного уравнения периодично, т.е. существует такое натуральное число t, что для любого x Î N 0 выполняется равенство d x + t = d x.
Доказательство. В силу теоремы 2 параграфа 3 достаточно доказать, что существуют такие натуральные числа k и l, что
d k = d l, d k + 1 = d l + 1, …, d k + n - 1 = d l + n - 1. (1)
Так как всего различных наборов вида (b 1, b 2,…, bn)над полем Fp конечно и равно pn. Поэтому, если k > l и t = k - l наименьшее число со свойством (1), то t £ pn -1.
Определение 1. Наименьший натуральный период t решения d линейного рекуррентного уравнения называется примитивным периодом решения d. Обозначаем примитивный период решения d через per d.
Теорема 2. Если F = Fp, d = {d x }Î s F (f), f Î Fp [l], то per d £ pn -1.
Доказательство. Число различных наборов (d0, d1,…, d n - 1) равно pn. Если (d0, d1,…, d n - 1) = (0, 0, …, 0), то d = {0} и per d = 1 £ pn -1.
Если (d0, d1,…, d n - 1) ¹ (0, 0,…,0), то для любого x Î N 0 набор (d x, d x +1,…,d x + n - 1) ¹ (0, 0, …, 0), а число ненулевых наборов вида (d x, d x +1,…, d x + n - 1) равно pn -1. Поэтому даже, если все они встретятся, то при некотором t имеем (d0, d1,…, d n - 1) = (d t, d t +1,…, d t + n - 1). Следовательно, per d £ pn -1.
Аннулирующие многочлены
Определение 1. Многочлен f Î F [l] называется нормированным, если его старший коэффициент равен1.
Определение 2. Многочлен g Î F [l] называется аннулирующим последовательность d, если g (l)·d= 0.
Пусть F = Fp, A F (d) = A (d) – множество всех многочленов, аннулирующих последовательность d.
Пример 1. Пусть d решение уравнения
d x + n = a 1d x + n - 1 + a 2d x + n - 2 + …+ an d x (1)
t = per d. Тогда
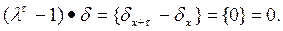
Таким образом, lt - 1 – аннулирующий многочлен решения d.
Теорема 1. Характеристический многочлен уравнения (1) аннулирует любое решение d уравнения (1).
Доказательство. Пусть d = {d x } – любое решение уравнения (1),
f (l) = l n - a 1l n- 1 - …+ an Î Fp [l]
- характеристический многочлен уравнения (1). Тогда для любого x Î N 0 имеем
f (l)·d = a = {a x },
где
a x = (Tn - a 1 T n- 1 - …+ an)·d x = a x = Tn ·d x - a 1 T n- 1·d x - …+ an d x =
= d x +n - a 1d x + n - 1-…- an d x = 0,
так как d - решение уравнения (1).
Теорема 2. Пусть d Î s – последовательность над полем Fp,
f (l) = l n - a 1l n - 1 - …+ an Î Fp [l]
- нормированный многочлен со свободным членом неравным нулю. Полиномиальный оператор f аннулирует последовательность d тогда и только тогда, когда d - решение линейного рекуррентного уравнения с характеристическим многочленом f.
Доказательство. Если d – решение уравнения (1), то по доказанному в теореме 1 полиномиальный оператор f аннулирует d.
Обратно пусть полиномиальный оператор f аннулирует d, т.е. f ·d = a = 0, т.о.
для любого x Î N 0 имеем
a x = (Tn - a 1 T n- 1 - …+ an)·d x = a x = Tn ·d x - a 1 T n- 1·d x - …+ an d x =
= d x +n - a 1d x + n - 1-…- an d x = 0.
Отсюда
d x +n = a 1d x + n - 1+…+ an d x
и d = {d x } – решение уравнения (1).
Теорема 3. Пусть d Î s (f), F = Fp; g, h Î A F (d) = A (d); q Î Fp [l]. Тогда:
1) g + h Î A F (d),
2) g - h Î A F (d),
3) gq Î A F (d).
Доказательство. Пусть g, h Î A F (d) = A (d); q Î Fp [l]. Тогда g ·d = 0, h ·d = 0. Тогда по теореме 4 параграфа 2 имеем
(g + h)·d = g ·d + h ·d = 0 + 0 = 0;
(g - h)·d = g ·d - h ·d = 0 - 0 = 0;
(gq)·d = q ·(g ·d)= q ·0 = 0.
Отсюда следует утверждение теоремы.
Определение 3. Минимальным многочленом последовательности d Î s (f) называется нормированный многочлен наименьшей степени из A (d).
Примеры. Если d = 0, то m d(l) = 1.
Если для любого x Î N 0 имеем d x +1 = d x и d x ¹ 0, то m d(l) = l -1.
d ¹ 0 тогда и только тогда, когда deg m d(l) ³ 1.
Теорема 4 (основное свойство минимального многочлена). Многочлен g Î Fp [l] принадлежит A F (d) тогда и только тогда, когда g делится на минимальный многочлен m d(l) решения d.
Доказательство. Необходимость.Пусть g Î A F (d). Докажем, что m d(l)| g. Допустим, что это не так. Тогда разделим g на m d(l) с остатком
g (l)= m d(l) q (l) + r (l),
где q (l), r (l)Î Fp [l], и deg r (l) < deg m d(l). Тогда
r (l)·d = (g (l)- m d(l) q (l))·d = g (l)·d- m d(l) q (l)·d = 0 + 0 = 0,
и r (l)Î A F (d) и deg r (l) ³ deg m d(l). Получаем противоречие.
Достаточность. Пусть m d(l)| g. Тогда g (l)= m d(l) q (l), где q (l)Î Fp [l].Тогда по теореме 4 параграфа 2 имеем
g ·d = (m d q)·d = q ·(m d·d) = q ·0 = 0.
Теорема 5. Минимальный многочлен главного решения уравнения (1) есть характеристический многочлен этого уравнения.
Доказательство. Пусть d – главное решение уравнения (1), m d(l) – минимальный многочлен d, f – характеристический многочлен уравнения (1). Так как f ·d = 0, то по теореме 4 m d(l)| f и, следовательно, deg m d(l) £ deg f. По определению главного решения последовательности d, T ·d,…, Tn - 1·d образуют базис пространства решений S (f). Так как для любого i = 1, 2,…, n -1
m d(l)·(Ti ·d) = Ti ·(m d(l)·d) = Ti ·0 = 0,
то многочлен m d(l) аннулирует любой элемент из S (f). Тогда S (f) Í S (m d). Поэтому число элементов в S (f) не меньше чем в S (m d):
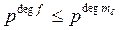 .
.
Следовательно, deg f £ deg m d(l). Отсюда deg m d(l) = deg f. Так как m d(l)| f и оба многочлена нормированные, то отсюда следует, что m d(l) = f.
Регистр сдвига
Определение 1. Регистром сдвига называют электронную схему, позволяющую вырабатывать последовательность, определяемую линейным рекуррентным уравнением.
Опишем электронную схему, физическая реализация которой позволяет вырабатывать псевдослучайную двоичную последовательность, задаваемую линейным рекуррентным уравнением. Схема состоит из элементов двух видов: один из них называется сумматором, а другой задержкой или ячейкой памяти.
Сумматор имеет два входа и один выход. Задержка имеет один вход и один выход. Они изображаются следующим образом:

Сумматор работает следующим образом: если на оба его входа подаются одинаковые сигналы (0 и 0 или 1 и 1), то на выход подается 0; если на оба его входа подаются разные сигналы (0 и 1 или 1 и 0), то на выход подается 1. Таким образом сумматор реализует сложение по mod 2.
Задержка работает следующим образом: если на вход задержки подается в данный момент времени какой-нибудь сигнал (0 или 1), то в следующий момент времени на ее выход подается тот же сигнал.
Пример 1. Рассмотрим схему, отвечающую уравнению
d x +4 = d x + d x +1 + d x +3.
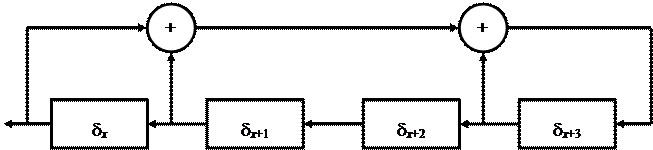 Выбирая первоначальное заполнение следующим образом:
Выбирая первоначальное заполнение следующим образом:
d0 = 1, d1 = 0, d2 = 1, d3 = 1,
получим периодическую последовательность: 10110110110… с наименьшим периодом, равным 3.
Пример 2. Рассмотрим схему, отвечающую уравнению
d x +4 = d x + d x +3.
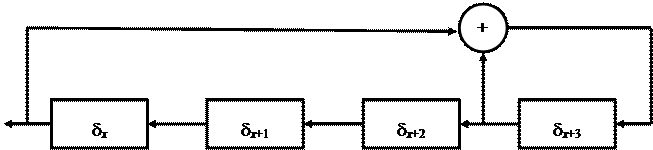 Выбирая первоначальное заполнение следующим образом:
Выбирая первоначальное заполнение следующим образом:
d0 = 1, d1 = 0, d2 = 1, d3 = 1,
получим периодическую последовательность: 10110010001111010110… с наименьшим периодом, равным 15.
Опишем электронную схему, физическая реализация которой позволяет вырабатывать псевдослучайную последовательность в любом конечном поле Z p, задаваемую линейным рекуррентным уравнением общего вида:
d x+n = a 1d x+n- 1 + a 2d x+n- 2 + …+ an d x (1)
Схема уже состоит из элементов трех видов: один из них называется сумматором, другой задержкой или ячейкой памяти, а третий умножитель.
Сумматор и задержка имеют тот же самый вид, что и выше.
Сумматор реализует сложение в поле Z p, т.е. сложение по mod p.
 Задержка работает следующим образом: если на вход задержки подается в данный момент времени какой-нибудь сигнал (0, 1,…, p -1), то в следующий момент времени на ее выход подается тот же сигнал.
Задержка работает следующим образом: если на вход задержки подается в данный момент времени какой-нибудь сигнал (0, 1,…, p -1), то в следующий момент времени на ее выход подается тот же сигнал.
Умножитель имеет один вход и один выход и имеет следующий вид: он реализует умножение элемента из поля Z p на элемент ai того же поля, т.е. умножение по mod p.
Пример 3. Рассмотрим схему, отвечающую уравнению
d x +4 = d x + d x +1 +2d x +3 в поле Z3
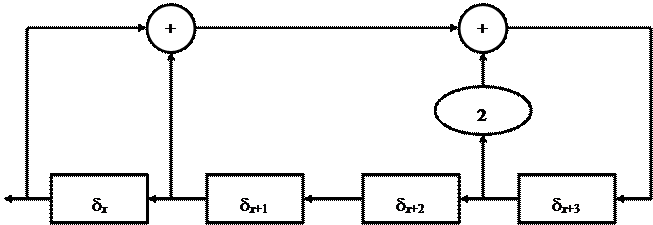
Выбирая первоначальное заполнение следующим образом:
d0 = 1, d1 = 0, d2 = 1, d3 = 1,
получим периодическую последовательность: 10110110110… с наименьшим периодом, равным 3.
Далее имеем
g·D x + y =g·(A x ·D y) = (B x ·g)·D y = g x ·D y .
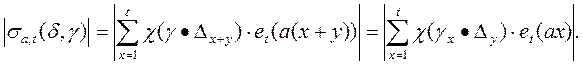
Следовательно,
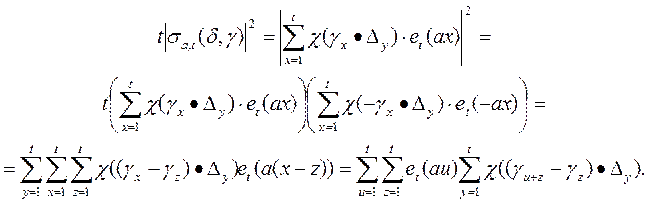
Отсюда находим
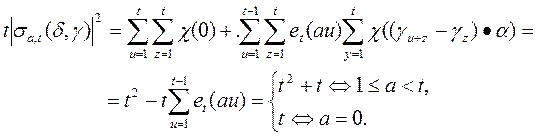
Таким образом,
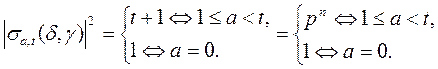
Теорема 2. Пусть f – примитивный многочлен степени n над полем Fp степени n; g Î Vn, g¹ 0; N – натуральное число;

Если 1 £ N £ t, то
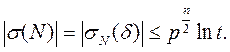
Доказательство. Имеем
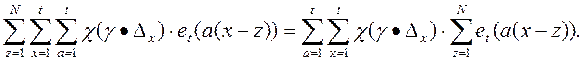
Из последнего получаем
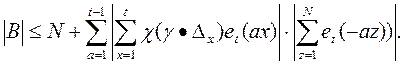
То получаем неравенство
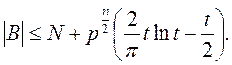
Тогда получаем

Теорема 3. Пусть f –примитивный многочлен над полем Fp степени n, d - ненулевое решение (1);
t = ord(f) = per d = pn – 1;
s, m 1, m 2, …, ms – натуральные числа с условиями:
1 £ s £ n, 0 £ m 1 < m 2 < … < ms < t;
b 1, b 2, …, bs – элементы поля Fp; N – натуральное число с условием 1 < N < t; TN = TN (b 1, b 2, …, bs; m 1, m 2, …, ms) – число решений в целых числах системы уравнений

Если 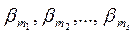 - линейно независимы над полем Fp, то
- линейно независимы над полем Fp, то
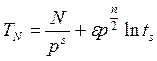 где |e| < 1.
где |e| < 1.
Где
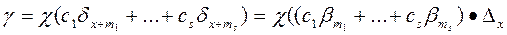 .
.
Но
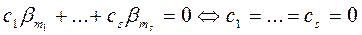 .
.
Поэтому

где внешняя сумма  берется по всем ненулевым комплексам (с 1,…, с s)
берется по всем ненулевым комплексам (с 1,…, с s)
440305
ПАМ
Толстиков А.В.
Лекция 10. Последовательности над конечными полями
1. Псевдослучайные последовательности и их применение в криптграфии..
2. Алгебра последовательностей над конечным полем.
3. Линейные рекуррентные последовательности над конечным полем.
4. Периодичность ЛРП. Длина периода ЛРП. Максимальные ЛРП.
5. Аннулирующие многочлены.
6. Вычисление длины периода ЛРП.
7. Регистр сдвига.
8. Число появлений наборов фиксированных знаков на полном периоде линейной рекуррентной последовательности.
9. Свойства решений линейного рекуррентного уравнения
10. Характеры групп и суммы характеров.
11. Максимальные линейные рекуррентные последовательности как псевдослучайные последовательности.
Литература. Нечаев В.И. – С. 49-60, 69-78, 85-87.
Глухов М.М. и др. -Т. 2. – С. 292-361.
Псевдослучайные последовательности и их применение в криптографии
Определение 1. Псевдослучайной последовательностью называют последовательность, конструируемую с помощью каких-либо арифметических алгоритмов.
Пример 1. Последовательность { an }, определяемая равенством
an = [p×10 n ] – 10×[p×10 n- 1].
| n
| 0
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11
| 12
| 13
| 14
|
| an
| 3
| 1
| 4
| 1
| 5
| 9
| 2
| 6
| 5
| 3
| 5
| 8
| 9
| 7
| 9
|
Пример 2. Последовательность { an }, определяемая равенством
an = [1/3×10 n ] – 10×[1/3×10 n- 1].
| n
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11
| 12
| 13
| 14
| 15
|
| an
| 1
| 4
| 2
| 8
| 5
| 7
| 1
| 4
| 2
| 8
| 5
| 7
| 1
| 4
| 2
|
Пример 3. Пусть a 0 = 0, a 1 = 1. Последовательность { an }, определяемая равенством
an = (an – 1 + an – 2) (mod 3)
| n
| 0
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11
| 12
| 13
| 14
|
| an
| 1
| 1
| 2
| 0
| 2
| 2
| 1
| 0
| 1
| 1
| 2
| 0
| 2
| 2
| 1
|
Периодические последовательности применяются при локации удаленных и быстродвижущихся объектов (планет, спутников, ракет). Чтобы определить положение объекта в атмосфере и пространстве, используется радиолокатор, антенна которого излучает электромагнитную энергию узким пучком и направление пучка меняется при перемещении антенны. Частота f излучения находится в пределах 2×108 – 1010 Гц а длина волны l = c / f - в пределах 0,03 – 1,5 м. При достижении пучка радиоволн объекта, часть его отражается обратно к антенне. Регистрация отраженного пучка, служит указанием наличия объекта в заданном направлении. Точное положение объекта в пространстве, только определив расстояние до него. Расстояние до объекта можно определить, измерив время между моментом излучения электромагнитного импульса и моментом прихода его отражения от объекта. С определением этого времени возникают трудности, так как объект перемещается в пространстве, а также в связи с тем, что в атмосфере возникают разные помехи. Поэтому ни посылка единичного импульса, ни серии одинаковых импульсов не содействуют решению этой задачи. Задача успешно решается посылкой длинной серии импульсов, закодированных таким образом, что она воспроизводит периодическую последовательность с очень большим периодом. В результате получив любой отраженный импульс, можно точно определить и момент его отправления и момент его получения. Приемная антенна, которая может совпадать с излучающей, должно имеет резко выраженное направление действия. Все это позволяет установить точное местоположение перемещающегося объекта. Период порядка 106 достаточен для локации луны, порядка 109 для локации Венеры.
|
| |  |
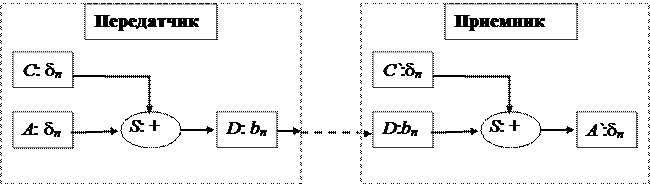
Периодические псевдослучайные последовательности применяются при передаче сколько угодно большого объема сообщений. Схема передачи состоит из передатчика и приемника. В передатчик входит преобразователь A, который всю поступающую информацию преобразует в двоичную последовательность { an } и передает ее в сумматор S. Устройство С вырабатывает псевдослучайную последовательность двоичных сигналов {d n } и передает ее в сумматор S. Эти обе двоичные последовательности складываются как элементы поля Z2, на выходе из сумматора получается последовательность { bn } = { an }+{d n } ={ an +d n }. Выходной преобразователь D преобразует последовательность в сери. электромагнитных импульсов и отправляет ее получателю. Переданная серия электромагнитных импульсов попадает в входной преобразователь D ` и преобразуется в последовательность { bn } и передает ее в сумматор S `. Устройство С` приемника вырабатывает псевдослучайную последовательность двоичных сигналов {d n } и передает ее в сумматор S `. Эти обе двоичные последовательности складываются как элементы поля Z2, на выходе из сумматора получается последовательность { с n } = { bn }+{d n } = { bn +d n } = { an +d n +d n } = { an }, которая отправляется в выходной преобразователь A `. В результате получатель получает отправленное сообщение. Для успешной работы этой схемы передачи сообщений необходимо, чтобы оба устройства A и A `работали синхронно иначе на выходе получается последовательность, отличная от { an }.



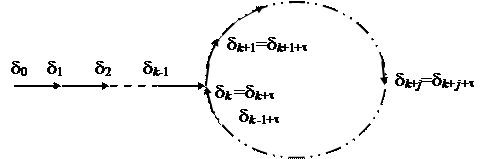
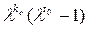 . Применяя теорему о вычислении НОД многочленов методом получим
. Применяя теорему о вычислении НОД многочленов методом получим ,
,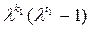 - линейная комбинация многочленов l k (l t -1)·d,
- линейная комбинация многочленов l k (l t -1)·d,  .
.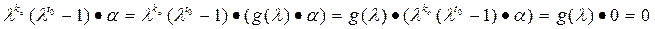 .
. Следовательно,
Следовательно,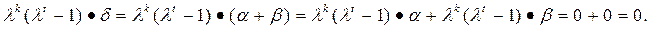
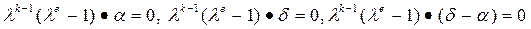 . Поэтому
. Поэтому 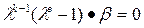 и по теореме 1 k (b)£ k – 1. Что невозможно. Следовательно, k (d) = k и формула (5) доказана.
и по теореме 1 k (b)£ k – 1. Что невозможно. Следовательно, k (d) = k и формула (5) доказана. .
.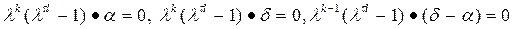 .
. и по теореме 1 t (b) | t l. Так как (t (b), l) = 1, то t (b) | t. Аналогично доказывает.
и по теореме 1 t (b) | t l. Так как (t (b), l) = 1, то t (b) | t. Аналогично доказывает.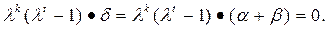
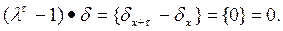
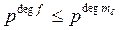 .
.
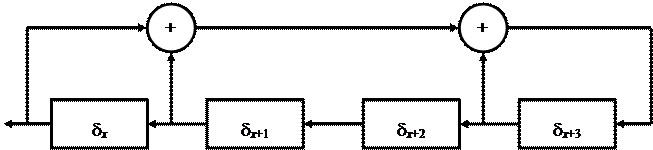 Выбирая первоначальное заполнение следующим образом:
Выбирая первоначальное заполнение следующим образом: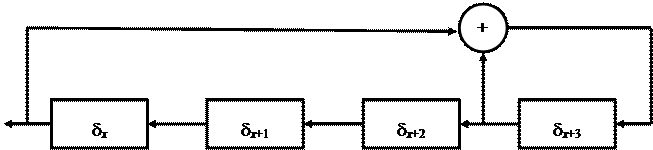 Выбирая первоначальное заполнение следующим образом:
Выбирая первоначальное заполнение следующим образом: Задержка работает следующим образом: если на вход задержки подается в данный момент времени какой-нибудь сигнал (0, 1,…, p -1), то в следующий момент времени на ее выход подается тот же сигнал.
Задержка работает следующим образом: если на вход задержки подается в данный момент времени какой-нибудь сигнал (0, 1,…, p -1), то в следующий момент времени на ее выход подается тот же сигнал.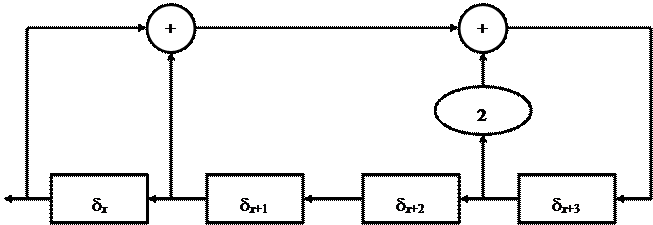
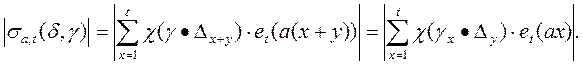
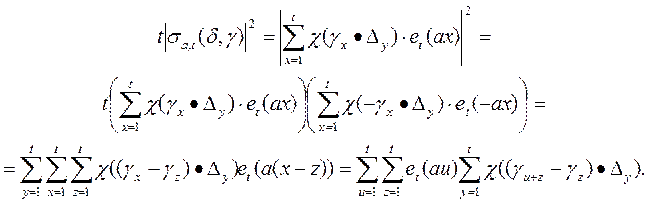
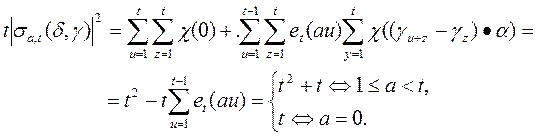
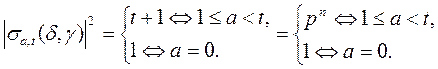

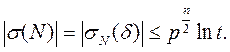
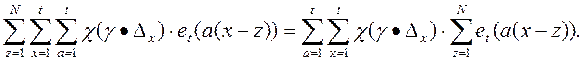
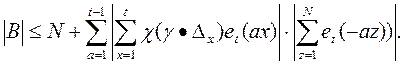
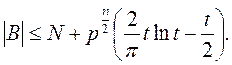


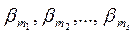 - линейно независимы над полем Fp, то
- линейно независимы над полем Fp, то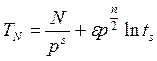 где |e| < 1.
где |e| < 1.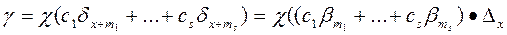 .
.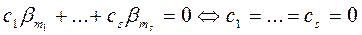 .
.
 берется по всем ненулевым комплексам (с 1,…, с s)
берется по всем ненулевым комплексам (с 1,…, с s)




