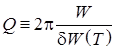Пусть испытывающее действие силы тяжести абсолютно твердое тело («физический маятник») массой m прикреплено к горизонтальной оси ращения О и обладает моментом инерции I относительно этой оси (рис.5.1). В начальный момент времени маятник отведен от положения равновесия на угол φ0 и ему сообщена начальная угловая скорость ω0. В текущий момент времени положение центра масс описывается радиус-вектором R, который составляет угол φ(t) с вертикалью. Требуется рассчитать зависимость от времени угла отклонения физического маятника.
, 
Рис.5.1. Физический маятник
Дифференциальное уравнение свободных незатухающих колебаний математического маятника непосредственно следует из уравнения (4.13) для углового ускорения абсолютно твердого тела с закрепленной осью вращения:
 , (5.1)
, (5.1)
где I - момент инерции тела относительно закрепленной оси вращения, R – расстояние от оси вращения до центра масс. Получившееся уравнение движения является нелинейным дифференциальным уравнением и не может быть решено хорошо развитыми стандартными решения линейных дифференциальных уравнений. Наиболее естественным методом решения уравнения (5.1) является его численное интегрирование с учетом начальных условий. Однако, в случае малых углов отклонения целесообразно упрощение левой части sin φ ≈ φ, превращающее (5.1) в обыкновенное линейное однородное дифференциальное уравнение второго порядка стандартного вида:
 . (5.2)
. (5.2)
Уравнение типа (5.2) весьма часто встречается в классической физике, поскольку хорошо описывает поведения большинства линейных систем, находящихся вблизи точки устойчивого равновесия.
В точках устойчивого равновесия x 0 потенциальная энергия одномерной системы U (x) обязательно имеет минимум (возможно локальный) и, следовательно, в малых окрестностях таких точек x = x 0 +Δ x хорошо аппроксимируется квадратичной параболой:
 ,
,
что означает существование в этой области возвращающей силы, линейной по величине смещения от точки устойчивого равновесия: Fx ≈ -k Δ x. Подстановка такого приближенного выражения для силы в классическое уравнение движения приводит к дифференциальному уравнению, полностью аналогичному (5.2).
Для придания исследуемому уравнению возможно наиболее общего вида и следуя традициям теоретической механики при записи однородного линейного дифференциального уравнения второго порядка (уравнения свободных колебаний) будет использоваться обобщенная координата q, под которой (в зависимости от конкретики задачи) может подразумеваться любая удобная для описания характеристика положения тела (одна из декартовых координат, угол отклонения, угол поворота и т.д.):
 . (5.3)
. (5.3)
Для большей общности в уравнение (5.3) введено дополнительное линейное по скорости слагаемое, соответствующее линейным по скорости диссипативным силам (например, силе вязкого трения при малых скоростях движения).
Для обеспечения однозначности решения уравнение (5.3) должно быть дополнено двумя начальными условиями (начальным положением и начальной скоростью).
Решение уравнение движения вида (5.3) удобно искать в комплексной форме. При желании такая запись полученного решения может быть проиллюстрирована с помощью векторных диаграмм, по сути являющихся относительно наглядным способом изображения решений на комплексной плоскости. Переход между комплексной и вещественной записью решений как правило осуществляется с помощью формул Эйлера, связывающих тригонометрические функции с экспонентами с комплексными показателями.

| Теорема 5.1. Формулы Эйлера. Обобщения понятий тригонометрических и экспоненциальных функций на случай комплексных аргументов вводятся согласно соотношениям:
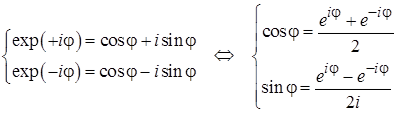 (5.4) (5.4)
|
5.2. Решение простейшего уравнения незатухающих
гармонических колебаний
Незатухающие колебания возникают в случае отсутствия диссипативных сил. Полная постановка задачи на расчет гармонических колебаний в наиболее общем виде.
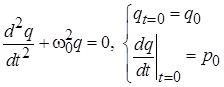 . (5.4)
. (5.4)
Стандартное пробное решение в виде экспоненты приводит (5.4) к характеристическому уравнению для ее показателя, оба корня которого оказываются чисто мнимыми:
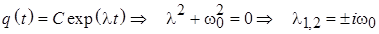 . (5.5)
. (5.5)
Общее решение уравнения однородного дифференциального уравнения второго порядка (5.4) строится как линейная комбинация двух построенных независимых пробных решений, с показателями степеней из (5.5), коэффициенты которой находятся из начальных условий:


Полное решение задачи (5.4) имеет вид:
 (5.6)
(5.6)
Легко убедиться, что в случае свободных незатухающих колебаний их полная механическая энергия не изменяется во времени.
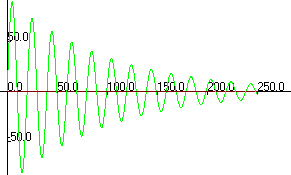
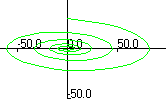
Удобным способом представления одномерного движения является его фазовый портрет - график зависимости скорости (или импульса) от координаты: p (q). В случае свободных незатухающих гармонических колебаний фазовый портрет представляет собой эллипс:
 .
.

Рис.5.2. Представление свободных незатухающих колебаний
с помощью зависимостей от времени обобщенных координат системы
и ее скоростей и фазового портрета
Затухающие колебания
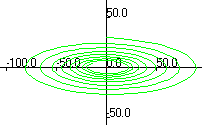
Учет действия диссипативных сил (например, линейной по скорости силы вязкого трения) делает колебания затухающими, фазовый портрет которых перестает быть замкнутой кривой, превращаясь в скручивающуюся спираль (рис. 5.3)
Уравнение движения линейного осциллятора при наличии вязкого трения (5.3) проще решать в частном случае начальных условий, соответствующих случаю кратковременного толчка системы, первоначально покоившейся в положении равновесия: q (0) = 0, p (0) = p 0.
В случае действия диссипативных сил характеристическое уравнение и его корни приобретают вид:
 . (5.7)
. (5.7)
В результате общее решение однородного уравнения (11.3) усложняется по сравнению с (5.5):
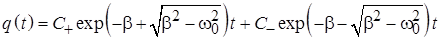 (5.8)
(5.8)
В случае малых величин диссипативных сил корни характеристического уравнения (5.7) оказываются комплексными, а решение (5.8) описывает затухающие колебания.
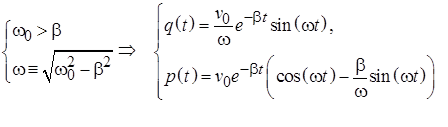 . (5.9)
. (5.9)
Частота затухающих колебаний (5.9) оказывается меньше частоты колебаний в случае отсутствия энергетических потерь (5.6). Появление нового эффекта уменьшения амплитуды колебаний с течением времени предопределяет ведение новых дополнительных характеристик процесса. Временем жизни колебаний называется временной интервал на котором амплитуда колебаний уменьшается в e раз:
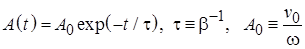 .
.
Легко заметить, что время жизни процесса определяется отношением массы совершающего колебания тела к эффективному коэффициенту вязкого трения.
Другой популярной характеристикой процесса затухания колебаний я является логарифмический декремент затухания:
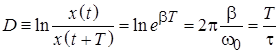 .
.
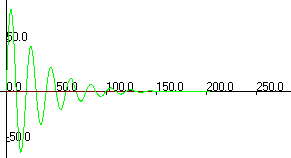
Добротностью осциллятора называется отношение запасенной энергии к энергии, теряемой за период):
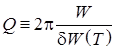
Добротность просто выражается через с логарифмическим декрементом затухания (обязательно найдите эту связь!).
Рис. 5.3. Затухающие колебания и их фазовые портреты
при различных коэффициентах вязкого трения




 , (5.1)
, (5.1) . (5.2)
. (5.2) ,
, . (5.3)
. (5.3)
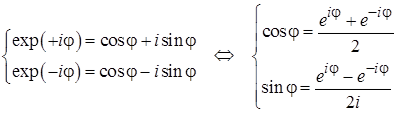 (5.4)
(5.4)
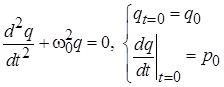 . (5.4)
. (5.4)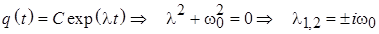 . (5.5)
. (5.5)

 (5.6)
(5.6) .
. 
 . (5.7)
. (5.7)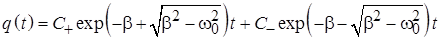 (5.8)
(5.8)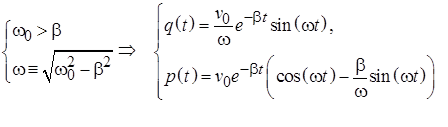 . (5.9)
. (5.9)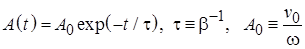 .
.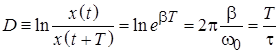 .
.