Конечная разность «вперед» для таблично заданной функции в i -той точке определяется выражением:  , где функция
, где функция  задана, как функция целочисленного аргумента с единичным шагом по аргументу i.
задана, как функция целочисленного аргумента с единичным шагом по аргументу i.
Для аналитически заданной и протабулированной с постоянным шагом h функции  определяющее соотношение имеет вид:
определяющее соотношение имеет вид:
 .
.
Преобразование таблицы функции  в функцию целочисленного аргумента
в функцию целочисленного аргумента  осуществляют при помощи линейного соотношения между аргументами x и i:
осуществляют при помощи линейного соотношения между аргументами x и i:  .
.
Коэффициенты a и b находят из системы уравнений, получаемой в результате подстановки в пределах заданной таблицы вместо x и i сначала начальных значений аргументов  , а затем конечных
, а затем конечных  . При этом начало таблицы удобно совместить с началом координат функции с целочисленным аргументом
. При этом начало таблицы удобно совместить с началом координат функции с целочисленным аргументом  (
( ). Тогда для таблицы с (n+ 1) – й строками:
). Тогда для таблицы с (n+ 1) – й строками:
 ,
,

Повторные конечные разности n -го порядка в i -той точке для табличной функции  определяются соотношением
определяются соотношением
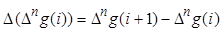 .
.
Конечно-разностные операторы
Линейность конечно-разностного оператора 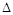 позволяет ввести конечно-разностный оператор сдвига
позволяет ввести конечно-разностный оператор сдвига  и многочлены от оператора
и многочлены от оператора 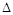 с целыми коэффициентами, такие, как
с целыми коэффициентами, такие, как  , где
, где  должно рассматриваться как оператор повторной разности k -того порядка.
должно рассматриваться как оператор повторной разности k -того порядка.
Действие любого многочлена  на функцию g (i) определяется как
на функцию g (i) определяется как
 .
.
Применение оператора сдвига к g (i) преобразует последнее в g (i +1):
g (i +1) = E g (i) = (1+  ) g (i) = g (i) +
) g (i) = g (i) +  g (i).
g (i).
Повторное применение оператора сдвига позволяет выразить (i+n) – е значение ординаты функции g через конечные разности различных порядков:
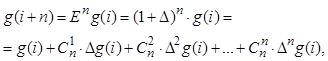
где  – число сочетаний из n элементов по k;
– число сочетаний из n элементов по k;
 – многочлен степени k от целой переменной n (
– многочлен степени k от целой переменной n (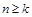 ), имеющий k сомножителей. При k=n
), имеющий k сомножителей. При k=n  .
.
В силу линейности оператора сдвига можно конечно-разностный оператор выразить, как  , и определить повторные конечные разности через многочлены от операторов сдвига так
, и определить повторные конечные разности через многочлены от операторов сдвига так  .
.
Последнее позволяет формульно выражать n -ную повторную разность через (n +1) ординату табличной функции, начиная с i -той строки:

Если в выражении для g (i+n) положить i =0 и вместо  подставить их факториальные представления, то после несложных преобразований получится разложение функции целочисленного аргумента по многочленам
подставить их факториальные представления, то после несложных преобразований получится разложение функции целочисленного аргумента по многочленам 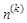 , которые в литературе называют факториальными:
, которые в литературе называют факториальными:
 .
.
Можно поставить задачу разложения и функции действительной переменной f (x) по многочленам  относительно начала координат (аналогично ряду Маклорена), т.е.
относительно начала координат (аналогично ряду Маклорена), т.е.  . Если последовательно находить конечные разности от левой и правой частей, то, зная, что
. Если последовательно находить конечные разности от левой и правой частей, то, зная, что  и
и  , после подстановки x =0 будем получать выражения для коэффициентов разложения
, после подстановки x =0 будем получать выражения для коэффициентов разложения  . У многочленов k -той степени,
. У многочленов k -той степени,  , поэтому
, поэтому
 .
.
Такое разложение табличной функции f (x) в литературе называют интерполяционным многочленом Ньютона для равных интервалов.



 , где функция
, где функция  задана, как функция целочисленного аргумента с единичным шагом по аргументу i.
задана, как функция целочисленного аргумента с единичным шагом по аргументу i. определяющее соотношение имеет вид:
определяющее соотношение имеет вид: .
. осуществляют при помощи линейного соотношения между аргументами x и i:
осуществляют при помощи линейного соотношения между аргументами x и i:  .
. , а затем конечных
, а затем конечных  . При этом начало таблицы удобно совместить с началом координат функции с целочисленным аргументом
. При этом начало таблицы удобно совместить с началом координат функции с целочисленным аргументом  (
( ). Тогда для таблицы с (n+ 1) – й строками:
). Тогда для таблицы с (n+ 1) – й строками: ,
,
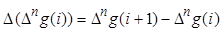 .
.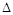 позволяет ввести конечно-разностный оператор сдвига
позволяет ввести конечно-разностный оператор сдвига  и многочлены от оператора
и многочлены от оператора  , где
, где  должно рассматриваться как оператор повторной разности k -того порядка.
должно рассматриваться как оператор повторной разности k -того порядка. на функцию g (i) определяется как
на функцию g (i) определяется как .
. ) g (i) = g (i) +
) g (i) = g (i) + 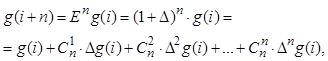
 – число сочетаний из n элементов по k;
– число сочетаний из n элементов по k; – многочлен степени k от целой переменной n (
– многочлен степени k от целой переменной n (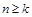 ), имеющий k сомножителей. При k=n
), имеющий k сомножителей. При k=n  .
. , и определить повторные конечные разности через многочлены от операторов сдвига так
, и определить повторные конечные разности через многочлены от операторов сдвига так  .
.
 подставить их факториальные представления, то после несложных преобразований получится разложение функции целочисленного аргумента по многочленам
подставить их факториальные представления, то после несложных преобразований получится разложение функции целочисленного аргумента по многочленам 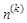 , которые в литературе называют факториальными:
, которые в литературе называют факториальными: .
. относительно начала координат (аналогично ряду Маклорена), т.е.
относительно начала координат (аналогично ряду Маклорена), т.е.  . Если последовательно находить конечные разности от левой и правой частей, то, зная, что
. Если последовательно находить конечные разности от левой и правой частей, то, зная, что  и
и  , после подстановки x =0 будем получать выражения для коэффициентов разложения
, после подстановки x =0 будем получать выражения для коэффициентов разложения  . У многочленов k -той степени,
. У многочленов k -той степени,  , поэтому
, поэтому .
.


