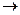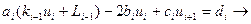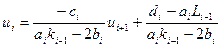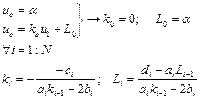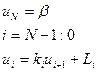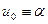Численное решение обыкновенных дифференциальных уравнений

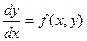
 (1)
(1)
Поле направлений — геометрическая интерпретация множества линейных элементов, соответствующих системе обыкновенных дифференциальных уравнений. Любая интегральная кривая системы обыкновенных дифференциальных уравнений в каждой своей точке касается отвечающего этой точке направления поля, и любая кривая, обладающая этим свойством, является интегральной кривой системы.
Задача Коши. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями, а точка 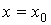 , в которой они задаются, – начальной точкой. Если дифференциальное уравнение n-го порядка, то для определения частного решения необходимо n начальных условий.
, в которой они задаются, – начальной точкой. Если дифференциальное уравнение n-го порядка, то для определения частного решения необходимо n начальных условий.
Пусть N- количество точек, i=1, 2, … N, тогда шаг 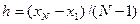
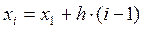
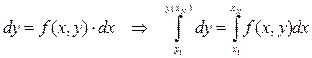
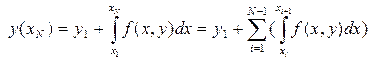
Если даны начальные условия: 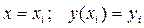 , то по разложению в ряд Тейлора:
, то по разложению в ряд Тейлора: 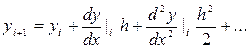 . Из уравнения (1) имеем
. Из уравнения (1) имеем 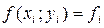
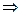
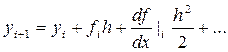
Метод интегрирования Эйлера первого порядка (n=1, O(h))
Метод интегрирования левых прямоугольников.
Начальные условия: 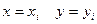
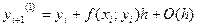
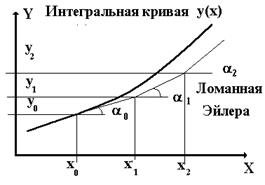

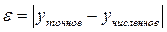
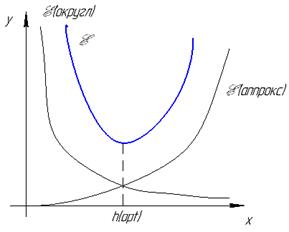
Для уменьшения погрешности необходимо уменьшить шаг, но с уменьшением шага растёт число округлений.
Усовершенствованный метод Эйлера (n=2)
Метод интегрирования трапеций
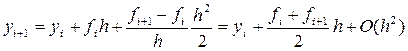
Для вычисления нового значения y необходимо посчитать два значения f, причём 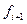 неизвестно
неизвестно 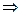 метод неявный. От неявности уходят следующим образом:
метод неявный. От неявности уходят следующим образом:

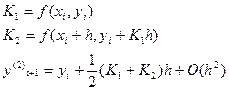
Чем выше порядок точности, тем меньше погрешность.
Модифицированный метод Эйлера (n=2)
Метод центральных прямоугольников
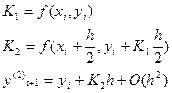
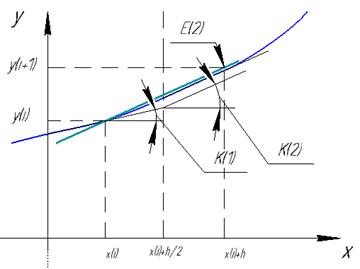
Метод Рунге-Кутта (n=4)
Метод парабол
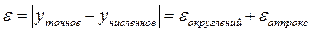
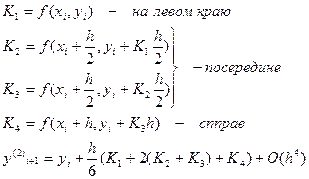
Линейные многошаговые методы интегрирования. Методы Адамса-Бэшфорта.
Явные методы, поскольку для вычисления нового y, следует посчитать f(k), более ранние значения известны.
1 порядок: 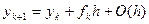
2 порядок: 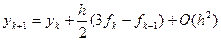
3 порядок: 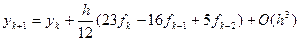
4 порядок: 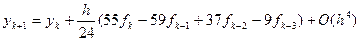
Погрешность вычислений:
Адамса-Бэшфорта 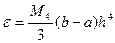
Рунге-Кутта 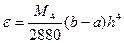
Следовательно, для достижения одинаковой точности в методе Адамса-Бэшфорта необходимо использовать более мелкий шаг, а потому он является менее экономичным.
Классификация методов интегрирования
1. По порядку точности. Порядок точности - наибольшая степень полинома, для которой численный метод даёт точное решение задачи.
2. Явные или неявные. Метод называется явным потому, что неизвестное значение может быть непосредственно вычислено по известному значению в предыдущей точке.
3. Одношаговые или многошаговые. В одношаговых методах для получения точки требуется лишь информация о последней рассчитанной точке. В m - шаговых методах для получения точки требуется информация о предыдущих m рассчитанных точках.
4. Самостартующие или несамостартающие. Самостартующий метод- метод, в котором для начала вычислений не требуется дополнительных расчётов.
Погрешности
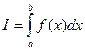 - точное значение интеграла
- точное значение интеграла
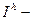 значение интеграла, рассчитываемое с шагом h
значение интеграла, рассчитываемое с шагом h
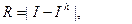
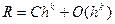
- 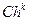 - главный член погрешности;
- главный член погрешности;
- 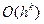 - второстепенный член погрешности.
- второстепенный член погрешности.
Например, 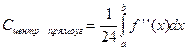
-даёт очень скруглённую величину, так как вместо каждой производной берётся одна максимальная;
- может быть вычислена до решения.
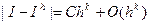
Предположим, что шаг уменьшен до 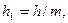 тогда
тогда 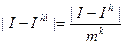
Следовательно, уменьшение сетки приводит к уменьшению погрешности.
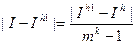
Cлева в формуле - априорная погрешность (теоретическая), справа- апостериорная (практическая). Эта формула даёт более точный результат.
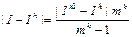
Для h1=h/2: 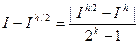 - формулы Рунге или формулы второго пересчёта.
- формулы Рунге или формулы второго пересчёта.
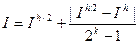 - экстраполяция Ричардсона.
- экстраполяция Ричардсона.
Метод стрельбы (пристрелки)
Перевод краевой задачи к последовательности решений задач Коши.
Пусть дано:
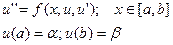
Зададим 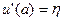
Приравняем 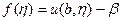 . Нужно подобрать значение производной на правой границе так, чтобы совпало численное решение и заданное условие
. Нужно подобрать значение производной на правой границе так, чтобы совпало численное решение и заданное условие 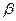 .
.
Конечно-разностный метод
Пусть дано
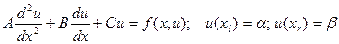
Выразим производные через разностное отношение и подставим в исходное уравнение, получим:
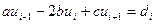 , где, в общем случае, a, b, с- f(h). Тогда получаем систему линейных уравнений:
, где, в общем случае, a, b, с- f(h). Тогда получаем систему линейных уравнений:
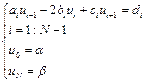 ; (1)
; (1)
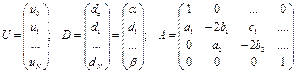 - ленточная матрица
- ленточная матрица
Скалярная прогонка
Состоит из двух этапов:
- - прямой прогонки - использует левое граничное условие и находит прогоночные коэффициенты K и L
- обратной прогонки
8N действий.
Необходимое условие устойчивости скалярной прогонки.
Должно выполняться правило диагонального преобладания:
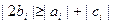 - модуль главной диагонали больше суммы модулей побочных диагоналей.
- модуль главной диагонали больше суммы модулей побочных диагоналей.
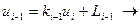 (1)
(1) 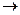
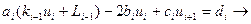
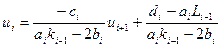
Прямая прогонка (Левое граничное условие)
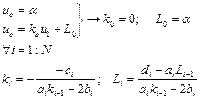
Обратная прогонка (Правое граничное условие)
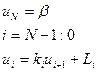
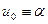
Численное решение обыкновенных дифференциальных уравнений

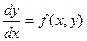
 (1)
(1)
Поле направлений — геометрическая интерпретация множества линейных элементов, соответствующих системе обыкновенных дифференциальных уравнений. Любая интегральная кривая системы обыкновенных дифференциальных уравнений в каждой своей точке касается отвечающего этой точке направления поля, и любая кривая, обладающая этим свойством, является интегральной кривой системы.
Задача Коши. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями, а точка 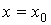 , в которой они задаются, – начальной точкой. Если дифференциальное уравнение n-го порядка, то для определения частного решения необходимо n начальных условий.
, в которой они задаются, – начальной точкой. Если дифференциальное уравнение n-го порядка, то для определения частного решения необходимо n начальных условий.
Пусть N- количество точек, i=1, 2, … N, тогда шаг 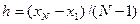
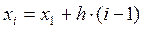
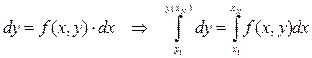
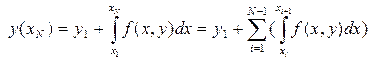
Если даны начальные условия: 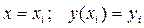 , то по разложению в ряд Тейлора:
, то по разложению в ряд Тейлора: 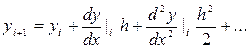 . Из уравнения (1) имеем
. Из уравнения (1) имеем 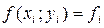
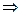
Метод интегрирования Эйлера первого порядка (n=1, O(h))
Метод интегрирования левых прямоугольников.
Начальные условия: 
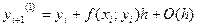


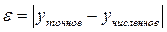
Для уменьшения погрешности необходимо уменьшить шаг, но с уменьшением шага растёт число округлений.
Усовершенствованный метод Эйлера (n=2)
Метод интегрирования трапеций
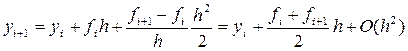
Для вычисления нового значения y необходимо посчитать два значения f, причём 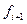 неизвестно
неизвестно 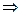 метод неявный. От неявности уходят следующим образом:
метод неявный. От неявности уходят следующим образом:

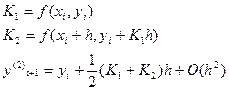
Чем выше порядок точности, тем меньше погрешность.
Модифицированный метод Эйлера (n=2)
Метод центральных прямоугольников
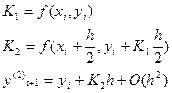

Метод Рунге-Кутта (n=4)
Метод парабол
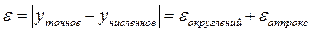
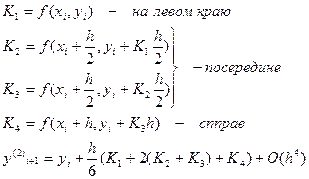





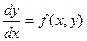
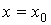 , в которой они задаются, – начальной точкой. Если дифференциальное уравнение n-го порядка, то для определения частного решения необходимо n начальных условий.
, в которой они задаются, – начальной точкой. Если дифференциальное уравнение n-го порядка, то для определения частного решения необходимо n начальных условий.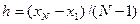
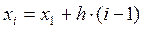
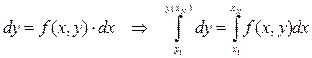
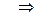
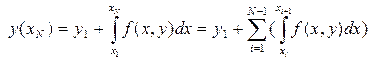
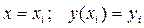 , то по разложению в ряд Тейлора:
, то по разложению в ряд Тейлора: 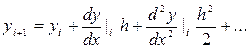 . Из уравнения (1) имеем
. Из уравнения (1) имеем 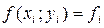
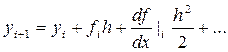
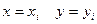
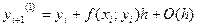

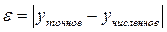
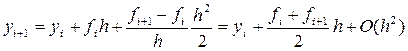
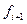 неизвестно
неизвестно 
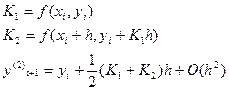
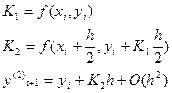

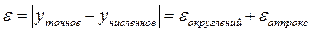
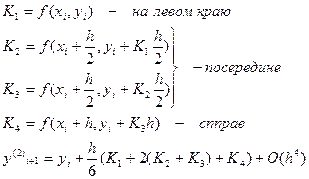

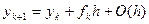
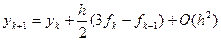
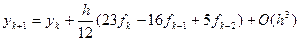
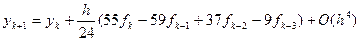
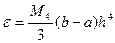
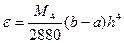
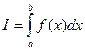 - точное значение интеграла
- точное значение интеграла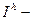 значение интеграла, рассчитываемое с шагом h
значение интеграла, рассчитываемое с шагом h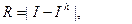
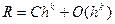
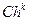 - главный член погрешности;
- главный член погрешности;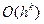 - второстепенный член погрешности.
- второстепенный член погрешности.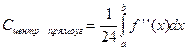
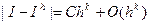
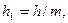 тогда
тогда 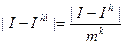
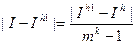
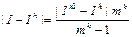
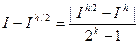 - формулы Рунге или формулы второго пересчёта.
- формулы Рунге или формулы второго пересчёта.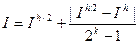 - экстраполяция Ричардсона.
- экстраполяция Ричардсона.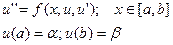
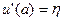
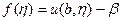 . Нужно подобрать значение производной на правой границе так, чтобы совпало численное решение и заданное условие
. Нужно подобрать значение производной на правой границе так, чтобы совпало численное решение и заданное условие 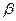 .
.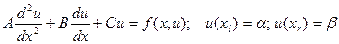
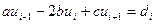 , где, в общем случае, a, b, с- f(h). Тогда получаем систему линейных уравнений:
, где, в общем случае, a, b, с- f(h). Тогда получаем систему линейных уравнений: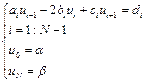 ; (1)
; (1)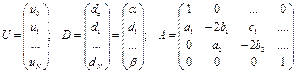 - ленточная матрица
- ленточная матрица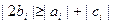 - модуль главной диагонали больше суммы модулей побочных диагоналей.
- модуль главной диагонали больше суммы модулей побочных диагоналей.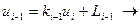 (1)
(1)