Методические указания
к проведению практических занятий по дисциплине
«Физика наноразмерных полупроводниковых структур»
Семинар 1
С1. Аналитический расчет короткоканального эффекта в МОПТ
План семинара
С1.1 Короткоканальный эффект
С1.2 Понижение барьера, индуцированное стоком (DIBL)
С1.3 Уравнение Пуассона и латеральное проникновение электрического поля
С1.4. Постановка проблемы aналитического решения уравнения Пуассона с упрощенными граничными условиями для расчета ККЭ в подпороговой области
С1.5 Метод решения
С1.6. Короткоканальный спад напряжения
С1.7. Анализ спада порогового напряжения
С1.8. Короткоканальный подпороговый наклон и чувствительность к подложке
С1.9. Экстремально ретроградное легирование (Ground-Plane) МОПТ
С1.10. Обобщенная длина масштабирования для high-k диэлектриков
Литература
Задание для СРС
Приложение 1 к семинару 1. Обобщенная модель длины масштабирования МОПТ
П1.1 Уравнение для длины масштабирования в модели двух областей
П1.2 Уравнение для длины масштабирования модели трех областей
П1.3 Ортогональность кусочно-линейных собственных функций
Литература к Приложению 1
С1.5 Метод решения
Метод решения использует принцип суперпозиции и заключается в представлении электростатического потенциала в виде следующих слагаемых:
 . (С1.11)
. (С1.11)
Здесь  − решение неоднородного уравнения (Пуассона), удовлетворяющее верхнему граничному условию (С1.5).
− решение неоднородного уравнения (Пуассона), удовлетворяющее верхнему граничному условию (С1.5).  ,
,  ,
, 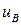 − решения однородного уравнении (Лапласа), выбранные надлежащим образом для удовлетворения остальным граничным условиям, а именно, на левой, правой и нижней стороне прямоугольного бокса на рис.С1.4. Например,
− решения однородного уравнении (Лапласа), выбранные надлежащим образом для удовлетворения остальным граничным условиям, а именно, на левой, правой и нижней стороне прямоугольного бокса на рис.С1.4. Например,  равно нулю на верхней, нижней и правой границах, но
равно нулю на верхней, нижней и правой границах, но  удовлетворяет левому граничному условию (С1.6). Подобным же образом,
удовлетворяет левому граничному условию (С1.6). Подобным же образом,  равно нулю на верхней, нижней и левой границах, но
равно нулю на верхней, нижней и левой границах, но  удовлетворяет правому граничному условию (С1.7) и т.д.
удовлетворяет правому граничному условию (С1.7) и т.д.
Естественным выбором для  [фактически
[фактически  ] является решение для одномерного МОПТ, использующее приближение полного обеднения:
] является решение для одномерного МОПТ, использующее приближение полного обеднения:
 для области окисла
для области окисла  , (С1.12)
, (С1.12)
и  для области кремния
для области кремния  . (С1.13)
. (С1.13)
Здесь  − длинноканальный поверхностный потенциал, который изменяется с напряжением
− длинноканальный поверхностный потенциал, который изменяется с напряжением  . Он связан с толщиной ОПЗ
. Он связан с толщиной ОПЗ  формулой
формулой
 , (С1.14)
, (С1.14)
чтобы удовлетворять выражению (С1.4). Заметим, что выражения (С1.12) и (С1.13) удовлетворяют верхнему и части CD нижнего граничных условий, [выражения (С1.5) и (С1.8)], и непрерывны при х = 0. Требование, чтобы  было непрерывно при х = 0, позволяет найти соотношение между
было непрерывно при х = 0, позволяет найти соотношение между  и
и  :
:
 , (С1.15)
, (С1.15)
где  определяется выражением (С1.14). Заметим, что выражение (С1.15) совпадает с выражением для смещения затвора в подпороговой области:
определяется выражением (С1.14). Заметим, что выражение (С1.15) совпадает с выражением для смещения затвора в подпороговой области:  .
.
Остальные слагаемые решения в (С1.11) имеют следующую форму
 , (С1.16)
, (С1.16)
 , (С1.17)
, (С1.17)
 . (С1.18)
. (С1.18)
Коэффициенты определяются из требования удовлетворения  граничным условиям. Например, на левой границе
граничным условиям. Например, на левой границе
 . (С1.19)
. (С1.19)
Для вычисления отдельных коэффициентов  выражение (С1.19) умножается на ортогональные собственные функции и интегрируется от −
выражение (С1.19) умножается на ортогональные собственные функции и интегрируется от −  до
до  :
:
 . (С1.20)
. (С1.20)
 определяется выражениями (С1.12) и (С1.13). Но граничное условие (С1.6) точно определяет
определяется выражениями (С1.12) и (С1.13). Но граничное условие (С1.6) точно определяет  только на отрезке
только на отрезке  . Чтобы дополнить значения
. Чтобы дополнить значения  для неустановленного точно промежутка вдоль отрезка НА на рис.С1.4, используется линейная интерполяция между значениями
для неустановленного точно промежутка вдоль отрезка НА на рис.С1.4, используется линейная интерполяция между значениями 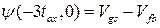 и
и 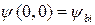 для отрезка
для отрезка 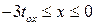 . Это хорошая аппроксимация, если ширина зазора
. Это хорошая аппроксимация, если ширина зазора  много меньше, чем
много меньше, чем  .
.
В середине прибора,  , члены в
, члены в  и
и 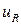 изменяются как
изменяются как  . Если длина канала L не слишком короткая, членами высокого порядка в обоих рядах можно пренебречь. Выполняя интегрирование в (С1.20) для n =1, получаем
. Если длина канала L не слишком короткая, членами высокого порядка в обоих рядах можно пренебречь. Выполняя интегрирование в (С1.20) для n =1, получаем
 , (С1.21)
, (С1.21)
где  . Так как
. Так как  мало по сравнению с
мало по сравнению с  , хорошей аппроксимацией является
, хорошей аппроксимацией является  , так что
, так что
 , (С1.22)
, (С1.22)
где  для 15°
для 15°  45°. Подобным же образом коэффициент наименьшего порядка в ряду
45°. Подобным же образом коэффициент наименьшего порядка в ряду  получается из правого граничного условия
получается из правого граничного условия
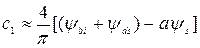 . (С1.23)
. (С1.23)
Третьим рядом,  , можно полностью пренебречь, так как граничное условие, выражение (С1.8), на большей части нижнего граничного условия (С D на рис. С1.4) уже удовлетворяет
, можно полностью пренебречь, так как граничное условие, выражение (С1.8), на большей части нижнего граничного условия (С D на рис. С1.4) уже удовлетворяет  , следовательно, и
, следовательно, и  . Остающийся вклад в коэффициент
. Остающийся вклад в коэффициент  от сегментов ВС и DE много меньше, чем
от сегментов ВС и DE много меньше, чем  или
или  .
.
Приближенное аналитическое решение для области кремния  в подпороговой области тогда
в подпороговой области тогда
 .(С1.24)
.(С1.24)
Вычисление поля  из вышеприведенного выражения показывает, что оно ведет себя так, как представлено на рис. С1.4(а) и (b). Характеристическая длина экспоненциального спада равна
из вышеприведенного выражения показывает, что оно ведет себя так, как представлено на рис. С1.4(а) и (b). Характеристическая длина экспоненциального спада равна 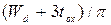 , и она масштабируется вместе с вертикальным размером прямоугольной области на рис. С1.4.
, и она масштабируется вместе с вертикальным размером прямоугольной области на рис. С1.4.
Литература
1. Taur, Y., Hu, G. J., Dennard, R H., Terman, L. M., Ting, C. Y. and Petrillo, K. E. (1985), A selfaligned 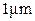 channel CMOS technology with retrograde n-well and thin epitaxy, IEEE Trans. Electron Devices ED-32, 203-209.
channel CMOS technology with retrograde n-well and thin epitaxy, IEEE Trans. Electron Devices ED-32, 203-209.
2. Troutman, R. R (1979). VLSI limitations from drain-induced barrier lowering, IEEE Trans. Electron Devices ED-26, 461-469.
3. Yuan Taur, Tak H. Ning, Fundamentals of Modern VLSI Device, Cambridge University Press, 2009.
4. Taur, Y., CMOS design near the limit of scaling, IBM J. RES. & DEV. VOL. 46 NO. 2/3 MARCH/MAY 2002, р. 213-221.
5. Nguyen, T. N. (1984). Small-geometry MOS transistors: physics and modeling of surface-and buried-channel MOSFETs. Ph. D. thesis, Stanford University.
6. Приложение 1. Обобщенная модель длины масштабирования МОПТ.
Задание для СРС
1. Ознакомиться с методические указаниями студентам по изучению дисциплины «Физика наноразмерных полупроводниковых структур» (Приложение 2).
2. Пользуясь материалом семинара №1 рассчитать величину короткоканального спада порогового напряжения и величину подпорогового размаха пМОПТ со следующими параметрами областей: 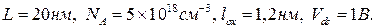
3. Самостоятельно изучить материал Приложения 1 к семинару 1.
4. Получить у преподавателя индивидуальное задание для подготовки реферата и выступления на семинаре.
Приложение 1 к семинару 1
Обобщенная модель характеристической длиныМОПТ
Рассмотренная на семинаре 1 модель характеристической длины называется моделью одной области. Она заменяет толщину окисла эквивалентной областью с той же диэлектрической проницаемостью, что и у кремния. но с толщиной, равной 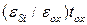 или
или 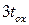 . Как указывалось, это корректно определяет нормальное поле (
. Как указывалось, это корректно определяет нормальное поле (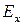 ), но тангенциальное поле (
), но тангенциальное поле (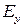 ) – некорректно. Модель одной области справедлива, только если толщина окисла много тоньше, чем характеристическая длина
) – некорректно. Модель одной области справедлива, только если толщина окисла много тоньше, чем характеристическая длина  , при котором в окисле преобладает нормальная компонента. В [1] опубликована модель обобщенной характеристической длины,которая распространяет модель одной области на две и три области с произвольными диэлектрическими постоянными и толщинами. Она рассматривает различные граничные условия для нормальных и тангенциальных полей отдельно на диэлектрических границах. Эти соотношения тогда приводят к уравнениям на собственные значения, которые могут быть решены для характеристической длины
, при котором в окисле преобладает нормальная компонента. В [1] опубликована модель обобщенной характеристической длины,которая распространяет модель одной области на две и три области с произвольными диэлектрическими постоянными и толщинами. Она рассматривает различные граничные условия для нормальных и тангенциальных полей отдельно на диэлектрических границах. Эти соотношения тогда приводят к уравнениям на собственные значения, которые могут быть решены для характеристической длины  в таких общих структурах.Обобщенная модель характеристической длиныочень важна для high-k диэлектриков, которые могут быть физически толстыми, а также и для КНИ и двухзатворных МОПТ.
в таких общих структурах.Обобщенная модель характеристической длиныочень важна для high-k диэлектриков, которые могут быть физически толстыми, а также и для КНИ и двухзатворных МОПТ.
П1.1 Уравнение для характеристической длиныв модели двух областей
В этом приложении описывается вывод обобщенной характеристической длиныМОПТ. Рассмотрим модель двух областей МОПТ, представленную на рис.П1.1. Предполагается, что область подзатворного изолятора имеет диэлектрическую проницаемость 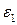 и толщину t 1. Обедненная область полупроводника имеет диэлектрическую проницаемость
и толщину t 1. Обедненная область полупроводника имеет диэлектрическую проницаемость 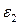 и толщину t 2. Заметим, что нижняя граница обедненной области упрощена до прямой линии тем же образом, как на рис.С1.4. В подпороговой области пренебрегается подвижными носителями в инверсной области. Электрический потенциал находится из решения двумерного уравнения Пуассона, примененного к прямоугольной области на рис П1.1.Существует проблема граничного условия, в которой требуется точно определить потенциал на четырех проводящих сторонах прямоугольника, левой (исток), верхней (затвор), правой (сток), нижней (подложка). Имеется реально два малых зазора, не огороженных проводниками: наверху слева между затвором и истоком и наверху справа между затвором и стоком. Когда эти зазоры не чрезмерно велики (по сравнению с, например,
и толщину t 2. Заметим, что нижняя граница обедненной области упрощена до прямой линии тем же образом, как на рис.С1.4. В подпороговой области пренебрегается подвижными носителями в инверсной области. Электрический потенциал находится из решения двумерного уравнения Пуассона, примененного к прямоугольной области на рис П1.1.Существует проблема граничного условия, в которой требуется точно определить потенциал на четырех проводящих сторонах прямоугольника, левой (исток), верхней (затвор), правой (сток), нижней (подложка). Имеется реально два малых зазора, не огороженных проводниками: наверху слева между затвором и истоком и наверху справа между затвором и стоком. Когда эти зазоры не чрезмерно велики (по сравнению с, например,  ), хорошим приближением является задание потенциала в виде линейной интерполяции между потенциалами затвора и истока для левого зазора и между потенциалами затвора и стока для правого зазора.
), хорошим приближением является задание потенциала в виде линейной интерполяции между потенциалами затвора и истока для левого зазора и между потенциалами затвора и стока для правого зазора.
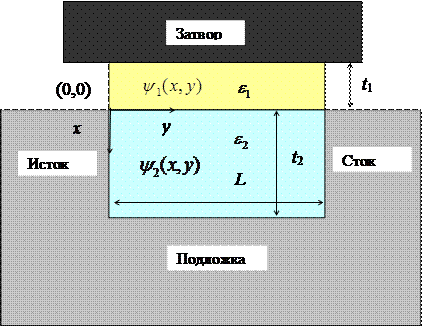 Используя тот же метод суперпозиции, что и в семинаре 1, решение для потенциала внутри выделенных областей,
Используя тот же метод суперпозиции, что и в семинаре 1, решение для потенциала внутри выделенных областей, 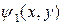 для области 1 и
для области 1 и 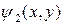 для области 2, может быть разложено на несколько компонент.
для области 2, может быть разложено на несколько компонент.
Рис П1.1Схематическая диаграмма МОПТ в модели двух областей.
Первая компонента – решение одномерного уравнения Пуассона в направлении х, которое удовлетворяет неоднородному (длинноканальному) уравнению и верхнему и нижнему граничным условиям. Другие два компонента являются решениями однородного двумерного уравнения Лапласа и выбраны для того, чтобы удовлетворить левому (исток) и правому (сток) граничным условиям, соответственно. В семинаре 1 показано, что последние члены ответственны за ККЭ. Левая (исток) и правая (сток) компоненты 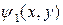 могут быть записаны как
могут быть записаны как
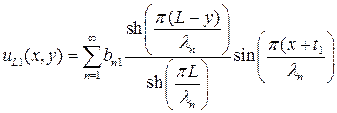 (П1.1)
(П1.1)
и 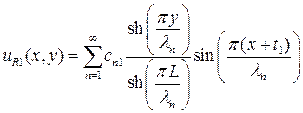 (П1.2)
(П1.2)
Заметим, что каждый член рядов 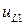 и
и 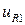 удовлетворяет уравнению Лапласа, например,
удовлетворяет уравнению Лапласа, например, 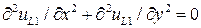 для любого
для любого  . Также заметим, что
. Также заметим, что 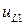 принимает нулевое значение на верхней (
принимает нулевое значение на верхней (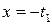 ) и правой (
) и правой (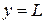 ) границах, в то время как
) границах, в то время как 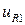 принимает нулевое значение на верхней и левой (
принимает нулевое значение на верхней и левой (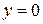 ) границах. Подобным же образом, левая и правая компоненты
) границах. Подобным же образом, левая и правая компоненты 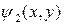 равны
равны
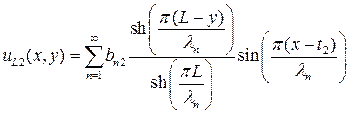 (П1.3)
(П1.3)
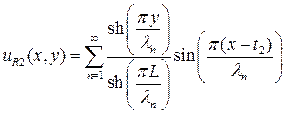 , (П1.4)
, (П1.4)
так что 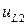 принимает нулевое значение на нижней (
принимает нулевое значение на нижней (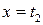 ) и правой (
) и правой (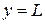 ) границах, в то время как
) границах, в то время как 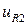 принимает нулевое значение на нижней и левой (
принимает нулевое значение на нижней и левой (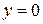 ) границах.
) границах.
На общей границе совместно для 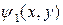 и
и 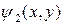 ,
, 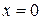 , при нормальном перемещении через границу величина
, при нормальном перемещении через границу величина 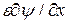 , также как потенциал
, также как потенциал 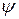 (следовательно, тангенциальное поле,
(следовательно, тангенциальное поле, 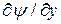 ) должны быть непрерывны при переходе из одной диэлектрической среды в другую. Вследствие различия формы функций от у, каждый член в
) должны быть непрерывны при переходе из одной диэлектрической среды в другую. Вследствие различия формы функций от у, каждый член в 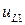 и
и 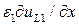 должен быть равен их аналогу в
должен быть равен их аналогу в 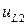 и
и 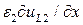 при
при 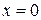 . Следовательно, получаем
. Следовательно, получаем
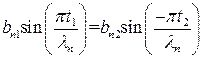 (П1.5)
(П1.5)
и 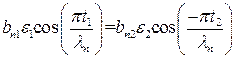 . (П1.6)
. (П1.6)
Подобные же соотношения получаются для 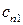 и
и 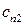 из
из 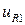 и
и 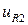 и их производных. Для ненулевых решений
и их производных. Для ненулевых решений 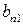 и
и 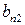 выражения (П1.5) и (П1.6) могут быть поделены друг на друга, чтобы получить уравнение для собственных значений
выражения (П1.5) и (П1.6) могут быть поделены друг на друга, чтобы получить уравнение для собственных значений 
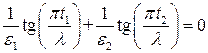 . (П1.7)
. (П1.7)
Здесь собственные значения, обозначенные как  , имеют дискретный ряд решений,
, имеют дискретный ряд решений, 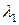 ,
, 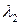 ,
, 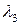 ,
, 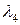 , в нисходящем порядке. Наибольшее собственное значение является и наиболее важным, так как каждый член короткоканального вклада в потенциал пропорционален
, в нисходящем порядке. Наибольшее собственное значение является и наиболее важным, так как каждый член короткоканального вклада в потенциал пропорционален  [смотри семинар 1, например, выражение (С1.26)]. В полной короткоканальной части потенциала доминирует член с наибольшим
[смотри семинар 1, например, выражение (С1.26)]. В полной короткоканальной части потенциала доминирует член с наибольшим  , то есть
, то есть 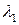 . Члены более высокого порядка в выражениях (П1.1) - (П1.4) пренебрежимо малы при условии, что длина канала не сравнима или короче, чем
. Члены более высокого порядка в выражениях (П1.1) - (П1.4) пренебрежимо малы при условии, что длина канала не сравнима или короче, чем 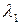 .
.
Для данных 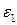 ,
, 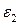 ,
, 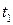 ,
, 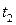 уравнение (П1.7) может бать решено относительно характеристической длины
уравнение (П1.7) может бать решено относительно характеристической длины  (используемой попеременно с
(используемой попеременно с 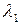 ), которая является эквивалентом двух областей вместо
), которая является эквивалентом двух областей вместо 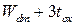 . ККЭ приемлемы, если
. ККЭ приемлемы, если 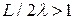 . Другими словами,
. Другими словами, 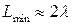 . Два важных случая нужно обсудить. Во-первых, для
. Два важных случая нужно обсудить. Во-первых, для 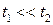 могут быть использованы приближения
могут быть использованы приближения 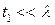 и
и 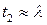 в уравнении (П1.7), чтобы получить
в уравнении (П1.7), чтобы получить 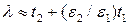 , что является приближением одной области на семинаре 1. Во-вторых, если
, что является приближением одной области на семинаре 1. Во-вторых, если 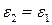 , наибольшее решение для
, наибольшее решение для  в (П1.7) есть просто
в (П1.7) есть просто 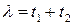 , полная физическая высота прямоугольного бокса на рис П1.1, как можно было и ожидать. В общем случае это позволяет интерпретировать
, полная физическая высота прямоугольного бокса на рис П1.1, как можно было и ожидать. В общем случае это позволяет интерпретировать  как диэлектрический эквивалент высоты полного бокса из двух областей, так что контроль ККЭ эквивалентен сохранению низкого аспектного отношения самого бокса.
как диэлектрический эквивалент высоты полного бокса из двух областей, так что контроль ККЭ эквивалентен сохранению низкого аспектного отношения самого бокса.
П1.2 Уравнение для характеристической длинымодели трех областей
Модель двух областей может быть распространена на структуру МОПТ с тремя областями, показанную на рис.П1.2. Следуя методу, изложенному выше, левые (исток) компоненты однородной части решения 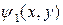 ,
, 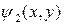 ,
, 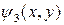 могут быть записаны как
могут быть записаны как
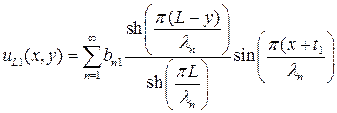 (П1.8)
(П1.8)
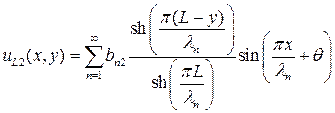 (П1.9)
(П1.9)
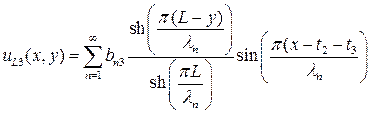 . (П1.10)
. (П1.10)
Заметим, что фаза синуса выбрана так, что 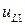 принимает нулевое значение на верхней границе, а
принимает нулевое значение на верхней границе, а 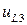 принимает нулевое значение на нижней границе. Фаза в
принимает нулевое значение на нижней границе. Фаза в 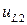 содержит дополнительную переменную
содержит дополнительную переменную 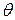 , определяемую позднее из граничных условий. Стоковые компоненты однородного решения могут быть выражены в форме, подобной выражениям (П1.2) и (П1.4). Они дают избыточные результаты, что касается уравнения для собственных значений.
, определяемую позднее из граничных условий. Стоковые компоненты однородного решения могут быть выражены в форме, подобной выражениям (П1.2) и (П1.4). Они дают избыточные результаты, что касается уравнения для собственных значений.
На границе между 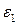 и
и 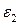 выполняются условия
выполняются условия 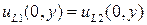 и
и 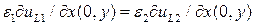 . Эти равенства к каждой паре соответствующих членов в двух рядах. Тогда их отношение дает
. Эти равенства к каждой паре соответствующих членов в двух рядах. Тогда их отношение дает
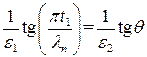 (П1.11)
(П1.11)
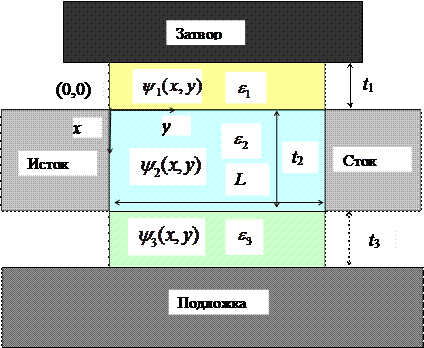
Рис.П1.2 Схематическая диаграмма МОПТ в модели трех областей.
На границе между 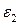 и
и 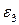 выполняются условия
выполняются условия 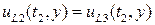 и
и 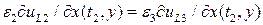 . Отношение соответствующих членов в двух рядах дает
. Отношение соответствующих членов в двух рядах дает
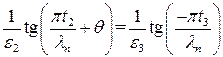 . (П1.12)
. (П1.12)
Исключая 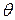 из выражений (П1.11) и (П1.12), получаем в результате уравнение собственных значений
из выражений (П1.11) и (П1.12), получаем в результате уравнение собственных значений  (или
(или  ) для трех областей
) для трех областей
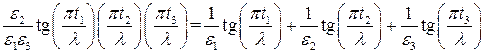 (П1.12)
(П1.12)
Решения есть 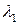 ,
, 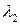 ,
, 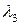 ,
, 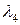 , в нисходящем порядке. Наибольшее собственное значение
, в нисходящем порядке. Наибольшее собственное значение 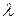 (используемое попеременно с
(используемое попеременно с 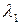 в лекциях и семинарах) есть эквивалентная длина масштабирования для трехслойной структуры на рис.П1.2. В специальном случае, когда
в лекциях и семинарах) есть эквивалентная длина масштабирования для трехслойной структуры на рис.П1.2. В специальном случае, когда 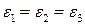 ,можно показать, что фундаментальное решение есть
,можно показать, что фундаментальное решение есть 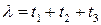 , как и ожидалось.
, как и ожидалось.
Модель характеристической длинытрех областей применима, например, для двухзатворных МОПТ и КНИ приборов с очень тонкими скрытыми слоями. Она может быть также применима в других случаях, замечая, что в то время как исток и сток предполагаются с диэлектрической постоянной 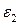 на рис П1.2, выражение (П1.13) равным образом справедливо, если исток и сток имеют диэлектрическую постоянную
на рис П1.2, выражение (П1.13) равным образом справедливо, если исток и сток имеют диэлектрическую постоянную 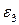 . Например, слой 3 может быть обедненной областью в объеме кремния, где находятся также исток и сток, и слои 1,2 представляют комбинированный изолятор затвора с различными диэлектрическими постоянными. В качестве альтернативы слой 2 может быть основанием изолятора затвора и слой 1 обедненной областью поликремниевого затвора.
. Например, слой 3 может быть обедненной областью в объеме кремния, где находятся также исток и сток, и слои 1,2 представляют комбинированный изолятор затвора с различными диэлектрическими постоянными. В качестве альтернативы слой 2 может быть основанием изолятора затвора и слой 1 обедненной областью поликремниевого затвора.
Литература
1. Frank, D. J., Taur, Y. and Wong, H.-S. (1998). Generalized scale length for two-dimensional effects in MOSFETs, IEEE Electron Device Lett. 19, 385-387.
2. Taur Y., CMOS design near the limit of scaling. IBM J. RES. & DEV. VOL. 46, NO. 2/3, 2002, pp.213-222.
3. Taur Y., Ning T.H., Fundamentals of Modern VLSI Device, 2009, Appendix 9, 10.
[1]  .Это технологически наиболее важный случай. Случай, когда глубина переходов стока и истока мельче, чем толщина ОПЗ под затвором, обсуждается в конце этого семинара.
.Это технологически наиболее важный случай. Случай, когда глубина переходов стока и истока мельче, чем толщина ОПЗ под затвором, обсуждается в конце этого семинара.
[2] 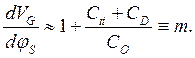 (3.1.2)
(3.1.2)
[3]  (С1.26)
(С1.26)
[4]  (3.1.6)
(3.1.6)
Методические указания
к проведению практических занятий по дисциплине
«Физика наноразмерных полупроводниковых структур»
Семинар 1
С1. Аналитический расчет короткоканального эффекта в МОПТ
План семинара
С1.1 Короткоканальный эффект
С1.2 Понижение барьера, индуцированное стоком (DIBL)
С1.3 Уравнение Пуассона и латеральное проникновение электрического поля
С1.4. Постановка проблемы aналитического решения уравнения Пуассона с упрощенными граничными условиями для расчета ККЭ в подпороговой области
С1.5 Метод решения
С1.6. Короткоканальный спад напряжения
С1.7. Анализ спада порогового напряжения
С1.8. Короткоканальный подпороговый наклон и чувствительность к подложке
С1.9. Экстремально ретроградное легирование (Ground-Plane) МОПТ
С1.10. Обобщенная длина масштабирования для high-k диэлектриков
Литература
Задание для СРС
Приложение 1 к семинару 1. Обобщенная модель длины масштабирования МОПТ
П1.1 Уравнение для длины масштабирования в модели двух областей
П1.2 Уравнение для длины масштабирования модели трех областей
П1.3 Ортогональность кусочно-линейных собственных функций
Литература к Приложению 1



 . (С1.11)
. (С1.11) − решение неоднородного уравнения (Пуассона), удовлетворяющее верхнему граничному условию (С1.5).
− решение неоднородного уравнения (Пуассона), удовлетворяющее верхнему граничному условию (С1.5).  ,
,  ,
, 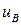 − решения однородного уравнении (Лапласа), выбранные надлежащим образом для удовлетворения остальным граничным условиям, а именно, на левой, правой и нижней стороне прямоугольного бокса на рис.С1.4. Например,
− решения однородного уравнении (Лапласа), выбранные надлежащим образом для удовлетворения остальным граничным условиям, а именно, на левой, правой и нижней стороне прямоугольного бокса на рис.С1.4. Например,  равно нулю на верхней, нижней и правой границах, но
равно нулю на верхней, нижней и правой границах, но  удовлетворяет левому граничному условию (С1.6). Подобным же образом,
удовлетворяет левому граничному условию (С1.6). Подобным же образом,  удовлетворяет правому граничному условию (С1.7) и т.д.
удовлетворяет правому граничному условию (С1.7) и т.д. ] является решение для одномерного МОПТ, использующее приближение полного обеднения:
] является решение для одномерного МОПТ, использующее приближение полного обеднения: для области окисла
для области окисла  , (С1.12)
, (С1.12) для области кремния
для области кремния  . (С1.13)
. (С1.13) − длинноканальный поверхностный потенциал, который изменяется с напряжением
− длинноканальный поверхностный потенциал, который изменяется с напряжением  . Он связан с толщиной ОПЗ
. Он связан с толщиной ОПЗ  формулой
формулой , (С1.14)
, (С1.14) было непрерывно при х = 0, позволяет найти соотношение между
было непрерывно при х = 0, позволяет найти соотношение между  , (С1.15)
, (С1.15) .
. , (С1.16)
, (С1.16) , (С1.17)
, (С1.17) . (С1.18)
. (С1.18) граничным условиям. Например, на левой границе
граничным условиям. Например, на левой границе . (С1.19)
. (С1.19) выражение (С1.19) умножается на ортогональные собственные функции и интегрируется от −
выражение (С1.19) умножается на ортогональные собственные функции и интегрируется от −  до
до  :
: . (С1.20)
. (С1.20) определяется выражениями (С1.12) и (С1.13). Но граничное условие (С1.6) точно определяет
определяется выражениями (С1.12) и (С1.13). Но граничное условие (С1.6) точно определяет  только на отрезке
только на отрезке  для неустановленного точно промежутка вдоль отрезка НА на рис.С1.4, используется линейная интерполяция между значениями
для неустановленного точно промежутка вдоль отрезка НА на рис.С1.4, используется линейная интерполяция между значениями 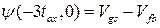 и
и 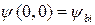 для отрезка
для отрезка 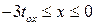 . Это хорошая аппроксимация, если ширина зазора
. Это хорошая аппроксимация, если ширина зазора  , члены в
, члены в  и
и 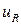 изменяются как
изменяются как  . Если длина канала L не слишком короткая, членами высокого порядка в обоих рядах можно пренебречь. Выполняя интегрирование в (С1.20) для n =1, получаем
. Если длина канала L не слишком короткая, членами высокого порядка в обоих рядах можно пренебречь. Выполняя интегрирование в (С1.20) для n =1, получаем , (С1.21)
, (С1.21) . Так как
. Так как  мало по сравнению с
мало по сравнению с  , хорошей аппроксимацией является
, хорошей аппроксимацией является  , так что
, так что , (С1.22)
, (С1.22) для 15°
для 15°  45°. Подобным же образом коэффициент наименьшего порядка в ряду
45°. Подобным же образом коэффициент наименьшего порядка в ряду  получается из правого граничного условия
получается из правого граничного условия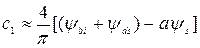 . (С1.23)
. (С1.23) , можно полностью пренебречь, так как граничное условие, выражение (С1.8), на большей части нижнего граничного условия (С D на рис. С1.4) уже удовлетворяет
, можно полностью пренебречь, так как граничное условие, выражение (С1.8), на большей части нижнего граничного условия (С D на рис. С1.4) уже удовлетворяет  , следовательно, и
, следовательно, и  . Остающийся вклад в коэффициент
. Остающийся вклад в коэффициент  от сегментов ВС и DE много меньше, чем
от сегментов ВС и DE много меньше, чем  или
или  .
. в подпороговой области тогда
в подпороговой области тогда .(С1.24)
.(С1.24) из вышеприведенного выражения показывает, что оно ведет себя так, как представлено на рис. С1.4(а) и (b). Характеристическая длина экспоненциального спада равна
из вышеприведенного выражения показывает, что оно ведет себя так, как представлено на рис. С1.4(а) и (b). Характеристическая длина экспоненциального спада равна 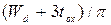 , и она масштабируется вместе с вертикальным размером прямоугольной области на рис. С1.4.
, и она масштабируется вместе с вертикальным размером прямоугольной области на рис. С1.4. channel CMOS technology with retrograde n-well and thin epitaxy, IEEE Trans. Electron Devices ED-32, 203-209.
channel CMOS technology with retrograde n-well and thin epitaxy, IEEE Trans. Electron Devices ED-32, 203-209.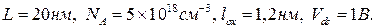
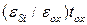 или
или 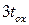 . Как указывалось, это корректно определяет нормальное поле (
. Как указывалось, это корректно определяет нормальное поле (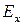 ), но тангенциальное поле (
), но тангенциальное поле (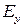 ) – некорректно. Модель одной области справедлива, только если толщина окисла много тоньше, чем характеристическая длина
) – некорректно. Модель одной области справедлива, только если толщина окисла много тоньше, чем характеристическая длина  , при котором в окисле преобладает нормальная компонента. В [1] опубликована модель обобщенной характеристической длины,которая распространяет модель одной области на две и три области с произвольными диэлектрическими постоянными и толщинами. Она рассматривает различные граничные условия для нормальных и тангенциальных полей отдельно на диэлектрических границах. Эти соотношения тогда приводят к уравнениям на собственные значения, которые могут быть решены для характеристической длины
, при котором в окисле преобладает нормальная компонента. В [1] опубликована модель обобщенной характеристической длины,которая распространяет модель одной области на две и три области с произвольными диэлектрическими постоянными и толщинами. Она рассматривает различные граничные условия для нормальных и тангенциальных полей отдельно на диэлектрических границах. Эти соотношения тогда приводят к уравнениям на собственные значения, которые могут быть решены для характеристической длины 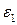 и толщину t 1. Обедненная область полупроводника имеет диэлектрическую проницаемость
и толщину t 1. Обедненная область полупроводника имеет диэлектрическую проницаемость 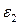 и толщину t 2. Заметим, что нижняя граница обедненной области упрощена до прямой линии тем же образом, как на рис.С1.4. В подпороговой области пренебрегается подвижными носителями в инверсной области. Электрический потенциал находится из решения двумерного уравнения Пуассона, примененного к прямоугольной области на рис П1.1.Существует проблема граничного условия, в которой требуется точно определить потенциал на четырех проводящих сторонах прямоугольника, левой (исток), верхней (затвор), правой (сток), нижней (подложка). Имеется реально два малых зазора, не огороженных проводниками: наверху слева между затвором и истоком и наверху справа между затвором и стоком. Когда эти зазоры не чрезмерно велики (по сравнению с, например,
и толщину t 2. Заметим, что нижняя граница обедненной области упрощена до прямой линии тем же образом, как на рис.С1.4. В подпороговой области пренебрегается подвижными носителями в инверсной области. Электрический потенциал находится из решения двумерного уравнения Пуассона, примененного к прямоугольной области на рис П1.1.Существует проблема граничного условия, в которой требуется точно определить потенциал на четырех проводящих сторонах прямоугольника, левой (исток), верхней (затвор), правой (сток), нижней (подложка). Имеется реально два малых зазора, не огороженных проводниками: наверху слева между затвором и истоком и наверху справа между затвором и стоком. Когда эти зазоры не чрезмерно велики (по сравнению с, например,  Используя тот же метод суперпозиции, что и в семинаре 1, решение для потенциала внутри выделенных областей,
Используя тот же метод суперпозиции, что и в семинаре 1, решение для потенциала внутри выделенных областей, 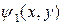 для области 1 и
для области 1 и 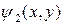 для области 2, может быть разложено на несколько компонент.
для области 2, может быть разложено на несколько компонент.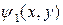 могут быть записаны как
могут быть записаны как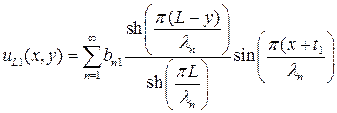 (П1.1)
(П1.1)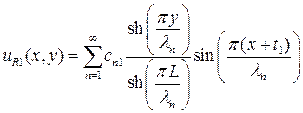 (П1.2)
(П1.2)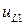 и
и 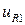 удовлетворяет уравнению Лапласа, например,
удовлетворяет уравнению Лапласа, например, 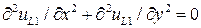 для любого
для любого  . Также заметим, что
. Также заметим, что 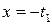 ) и правой (
) и правой (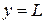 ) границах, в то время как
) границах, в то время как 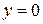 ) границах. Подобным же образом, левая и правая компоненты
) границах. Подобным же образом, левая и правая компоненты 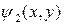 равны
равны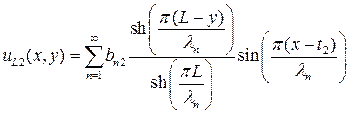 (П1.3)
(П1.3)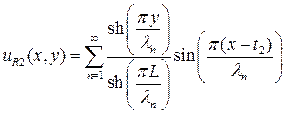 , (П1.4)
, (П1.4)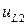 принимает нулевое значение на нижней (
принимает нулевое значение на нижней (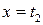 ) и правой (
) и правой (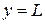 ) границах, в то время как
) границах, в то время как 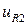 принимает нулевое значение на нижней и левой (
принимает нулевое значение на нижней и левой (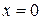 , при нормальном перемещении через границу величина
, при нормальном перемещении через границу величина 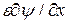 , также как потенциал
, также как потенциал 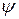 (следовательно, тангенциальное поле,
(следовательно, тангенциальное поле, 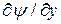 ) должны быть непрерывны при переходе из одной диэлектрической среды в другую. Вследствие различия формы функций от у, каждый член в
) должны быть непрерывны при переходе из одной диэлектрической среды в другую. Вследствие различия формы функций от у, каждый член в 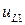 и
и 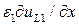 должен быть равен их аналогу в
должен быть равен их аналогу в 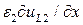 при
при 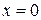 . Следовательно, получаем
. Следовательно, получаем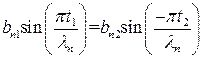 (П1.5)
(П1.5)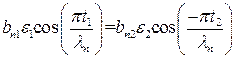 . (П1.6)
. (П1.6)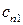 и
и 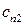 из
из 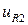 и их производных. Для ненулевых решений
и их производных. Для ненулевых решений 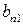 и
и 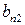 выражения (П1.5) и (П1.6) могут быть поделены друг на друга, чтобы получить уравнение для собственных значений
выражения (П1.5) и (П1.6) могут быть поделены друг на друга, чтобы получить уравнение для собственных значений 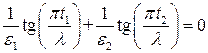 . (П1.7)
. (П1.7)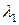 ,
, 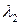 ,
, 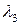 ,
, 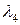 , в нисходящем порядке. Наибольшее собственное значение является и наиболее важным, так как каждый член короткоканального вклада в потенциал пропорционален
, в нисходящем порядке. Наибольшее собственное значение является и наиболее важным, так как каждый член короткоканального вклада в потенциал пропорционален  [смотри семинар 1, например, выражение (С1.26)]. В полной короткоканальной части потенциала доминирует член с наибольшим
[смотри семинар 1, например, выражение (С1.26)]. В полной короткоканальной части потенциала доминирует член с наибольшим 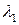 . Члены более высокого порядка в выражениях (П1.1) - (П1.4) пренебрежимо малы при условии, что длина канала не сравнима или короче, чем
. Члены более высокого порядка в выражениях (П1.1) - (П1.4) пренебрежимо малы при условии, что длина канала не сравнима или короче, чем 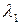 .
.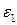 ,
, 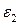 ,
, 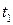 ,
, 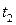 уравнение (П1.7) может бать решено относительно характеристической длины
уравнение (П1.7) может бать решено относительно характеристической длины 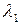 ), которая является эквивалентом двух областей вместо
), которая является эквивалентом двух областей вместо 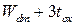 . ККЭ приемлемы, если
. ККЭ приемлемы, если 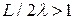 . Другими словами,
. Другими словами, 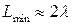 . Два важных случая нужно обсудить. Во-первых, для
. Два важных случая нужно обсудить. Во-первых, для 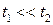 могут быть использованы приближения
могут быть использованы приближения 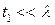 и
и 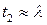 в уравнении (П1.7), чтобы получить
в уравнении (П1.7), чтобы получить 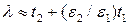 , что является приближением одной области на семинаре 1. Во-вторых, если
, что является приближением одной области на семинаре 1. Во-вторых, если 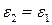 , наибольшее решение для
, наибольшее решение для 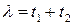 , полная физическая высота прямоугольного бокса на рис П1.1, как можно было и ожидать. В общем случае это позволяет интерпретировать
, полная физическая высота прямоугольного бокса на рис П1.1, как можно было и ожидать. В общем случае это позволяет интерпретировать 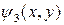 могут быть записаны как
могут быть записаны как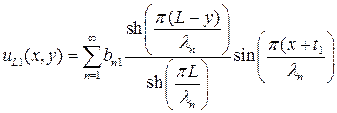 (П1.8)
(П1.8)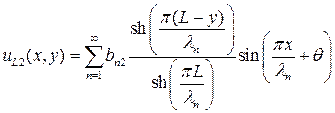 (П1.9)
(П1.9)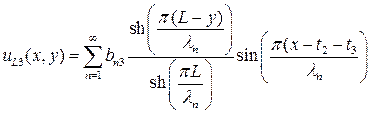 . (П1.10)
. (П1.10)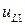 принимает нулевое значение на верхней границе, а
принимает нулевое значение на верхней границе, а 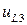 принимает нулевое значение на нижней границе. Фаза в
принимает нулевое значение на нижней границе. Фаза в 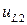 содержит дополнительную переменную
содержит дополнительную переменную 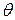 , определяемую позднее из граничных условий. Стоковые компоненты однородного решения могут быть выражены в форме, подобной выражениям (П1.2) и (П1.4). Они дают избыточные результаты, что касается уравнения для собственных значений.
, определяемую позднее из граничных условий. Стоковые компоненты однородного решения могут быть выражены в форме, подобной выражениям (П1.2) и (П1.4). Они дают избыточные результаты, что касается уравнения для собственных значений.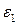 и
и 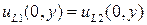 и
и 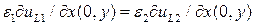 . Эти равенства к каждой паре соответствующих членов в двух рядах. Тогда их отношение дает
. Эти равенства к каждой паре соответствующих членов в двух рядах. Тогда их отношение дает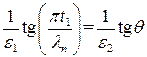 (П1.11)
(П1.11)
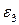 выполняются условия
выполняются условия 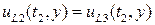 и
и 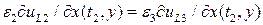 . Отношение соответствующих членов в двух рядах дает
. Отношение соответствующих членов в двух рядах дает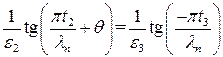 . (П1.12)
. (П1.12)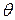 из выражений (П1.11) и (П1.12), получаем в результате уравнение собственных значений
из выражений (П1.11) и (П1.12), получаем в результате уравнение собственных значений 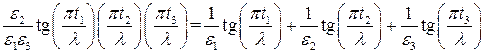 (П1.12)
(П1.12)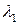 ,
, 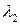 ,
, 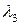 ,
, 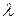 (используемое попеременно с
(используемое попеременно с 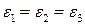 ,можно показать, что фундаментальное решение есть
,можно показать, что фундаментальное решение есть 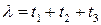 , как и ожидалось.
, как и ожидалось. .Это технологически наиболее важный случай. Случай, когда глубина переходов стока и истока мельче, чем толщина ОПЗ под затвором, обсуждается в конце этого семинара.
.Это технологически наиболее важный случай. Случай, когда глубина переходов стока и истока мельче, чем толщина ОПЗ под затвором, обсуждается в конце этого семинара.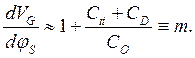 (3.1.2)
(3.1.2) (С1.26)
(С1.26) (3.1.6)
(3.1.6)


