Обработка и представление результатов многократных измерений

 

    Допустим, что было проведено  измерений некоторой величины x. Вследствие случайных факторов получится совокупность  различных значений одной и той же величины :

.

Эта совокупность значений получила название конечной выборки. Пусть максимальное измеренное значение равно , минимальное – . Представим результаты измерений в графической форме. Для этого предварительно проведём некоторую их обработку. Разобьём полный интервал изменения величины  на 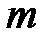 более мелких интервалов и введём величину интервала . Для каждого такого интервала определим количество измерений D n, для которых значение величины  попадает в рассматриваемый интервал. Определим величину   и построим график зависимости . Величина  в этом отношении определяет долю от общего числа измерений, приходящуюся на выбранный интервал. Пример такого графика приведён на рис. 12.1.

 

 

Рис. 12.1

 

    График представляет собой столбчатую диаграмму, которая называется гистограммой. Гистограмма достаточно наглядно демонстрирует как распределены значения результатов измерений: одни значения величины x в процессе измерений получались довольно редко, другие – более часто, а какие-то – очень часто. На некоторый интервал 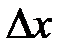 приходится максимальное значение величины .

Из опыта следует, что при увеличении числа измерений гистограмма будет принимать простую и вполне определённую форму, которая для множества различных экспериментов оказывается универсальной. Если совершить предельный переход: , , то гистограмма превратится в непрерывную кривую, которая описывается функцией следующего вида:

                                     .                                         (12.1)

Эта зависимость получила название функции распределения Гаусса или закона нормального распределения Гаусса. Её график изображён на рис. 12.2. Изображённая непрерывная кривая является, таким образом, предельным распределением или, как его ещё называют, генеральным распределением.

Предельное распределение – это теоретическая идеализация, к которой никогда нельзя абсолютно точно приблизиться в эксперименте. Чем больше количество измерений, тем ближе гистограмма к предельному распределению. Теоретическая идеализация, хотя и не достижима, очень важна: она демонстрирует предельные возможности распределения результатов в данном эксперименте. Если можно было получить в эксперименте предельное распределение, то информация, содержащаяся в нём, была максимально возможной и полной.

 

 

Рис. 12.2

 

Следует подчеркнуть, что не все предельные распределения имеют вид нормального распределения Гаусса. Но такое распределение чаще всего будет соответствовать Вашим экспериментальным данным. По этой причине мы рассматриваем именно это распределение.

Нормальное (генеральное) распределение характеризуется двумя параметрами:

1) генеральным средним значением ,

2) генеральным отклонением .

Генеральное среднее представляет собой то значение , на которое приходится максимум функции распределения Гаусса. Значения случайной величины  распределены относительно  симметрично (кривая нормального распределения имеет ось симметрии, проходящую через координату ).

Генеральное отклонение представляет собой меру ширины кривой нормального распределения. Чем меньше значение , тем быстрее уменьшается значение функции Гаусса по мере удаления значения  от величины генерального среднего, тем ýже кривая нормального распределения, меньше разброс значений измеряемой величины и, следовательно, точнее измерение.

Функция распределения Гаусса позволяет рассчитать долю измерений, приходящуюся на рассматриваемый интервал значений величины x:

                                                ,                                  (12.2)

где 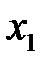 – нижняя граница выбранного интервала значений величины ,  – верхняя граница выбранного интервала значений величины .

Функция распределения Гаусса (12.1) удовлетворяет условию         нормировки:

.

Поэтому (12.2) можно интерпретировать как вероятность  того, что «истинное» значение измеряемой величины оказывается в рассматриваемом интервале. Из геометрического смысла интеграла следует, что площадь под кривой нормального распределения в пределах выбранного интервала (см. рис. 12.2), отнесенная к полной площади под всей кривой, должна давать величину этой вероятности и значение  соответственно.

Используя вероятностный смысл функции Гаусса, можно показать, что среднее значение измеряемой величины, определяемое как

,

в случае нормального распределения совпадает с , т.е. . Поэтому величина  и получила название среднего значения генерального (нормального) распределения или генерального среднего.

Аналогично можно показать, что значение   совпадает с величиной стандартного или среднеквадратичного отклонения, квадрат которого для нормального распределения определяется выражением

Поэтому   называется среднеквадратичным (стандартным) отклонением генерального (нормального) распределения или генеральным отклонением. Среднеквадратичноеотклонение характеризует среднюю меру разброса (отклонения) случайной величины  от среднего значения . Обратите внимание, сначала суммируются (интегрируются) значения величины 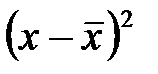 – квадраты всех отклонений от среднего. Квадратный корень из этой суммы и даёт величину среднеквадратичного отклонения. Если бы суммировались сами отклонения, т.е. величины , то в силу симметрии нормального распределения Гаусса результат был бы равен нулю. Это обусловлено тем, что отрицательные и положительные по знаку отклонения являются равновероятными. По этой причине вкачестве средней меры отклонения случайной величины от среднего используется именно среднеквадратичное отклонение.

Возьмём интервал , границы которого симметричны по отношению к генеральному среднему. Пользуясь (12.2), для нормального распределения можно определить вероятность p попадания «истинного» значения измеряемой величины в этот интервал. Если вероятность определена, то интервал называется доверительным интервалом измерения, а вероятность называют доверительной вероятностью или надёжностью измерения. Надёжность измерения выражается или в долях единицы или в процентах и зависит от величины выбранного интервала.

Если задан доверительный интервал с указанием величины надёжности (вероятности ), то информация о результатах измерения считается представленной с учётом случайных погрешностей измерения. Величина , характеризующая ширину доверительного интервала, называется доверительной погрешностью.

В качестве доверительного интервала для нормального распределения чаще всего используется интервал , связанный со стандартным отклонением. Величина доверительной вероятности для такого интервала составляет приблизительно 68,3%.

Если взять , то p = 95,5%. При  величина p = 99,7%. Последнее, например, означает, что вероятность обнаружить результат измерения величины x за пределами интервала  составляет всего 0,3%. Можно считать, что практически «истинное» значение измеряемой величины находится в этом интервале.

От функции распределения Гаусса, которая является теоретической предельной идеализацией, вернёмся к реальному распределению (см. рис. 12.1), в котором количество измерений  представляет собой конечную величину. Как в этом случае определяется доверительный интервал и представляются результаты измерений?

Аналогом величины  выступает величина выборочного среднего значения (среднеарифметического для конечной выборки):

                                                  .                                            (12.3)

Аналогом величины  является величина выборочного среднеквадратичного отклонения:

                                        .                                (12.4)

Чтобы получить оценку доверительного интервала для конечного числа измерений, приходится вводить величину   – коэффициент Стьюдента. Только введение этого коэффициента позволяет определить доверительную вероятность для заданного интервала значений или определить интервал для заданной величины вероятности. Последняя из этих двух операций более простая, поэтому в дальнейшем мы будем поступать именно так. Значения коэффициента Стьюдента для различных значений  и  определяются по специальной таблице, фрагмент которой имеет вид:

Таблица 12.1

(%)
	2	3	4	5	6	10	20	40
70	2,0	1,4	1,3	1,2	1,2	1,1	1,1	1,1
80	3,1	1,9	1,7	1,5	1,5	1,4	1,3	1,3
90	6,3	2,9	2,4	2,1	2,0	1,8	1,7	1,7
95	13,0	4,3	3,2	2,8	2,6	2,3	2,1	2,0
99	64,0	9,9	5,8	4,6	4,0	3,3	2,9	2,7

 

Задав необходимое значение надёжности измерения (вероятности ), находим по таблице величину , соответствующую проведённому количеству измерений . Например, для p = 80% при  значение .

Величина доверительной погрешности измерения находится по формуле:

                                                .                                          (12.5)

Чем большее значение надёжности измерения выбирается, тем больше значение коэффициента Стьюдента и тем больше ширина доверительного интервала (больше величина доверительной погрешности). С ростом числа измерений величина 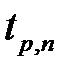 уменьшается.

Результат многократного измерения представляется в следующей форме:

 (n =..., p =...).

В скобках указывается количество измерений и значение доверительной вероятности, соответствующее доверительной погрешности.

Такая форма записи является наиболее информативной, так как она содержит данные не только о среднем значении измеренной величины и погрешности измерения, но и оценку надёжности результата.

Измерительные приборы вносят свой вклад в погрешность измерения, зависящий от точности прибора. Соответствующую величину принято называть приборной погрешностью. В общем случае она может иметь две составляющие – систематическую и случайную. У правильно настроенного и поверенного измерительного прибора систематическая погрешность либо отсутствует, либо является заранее известной.

Для определения приборной погрешности, связанной со случайными факторами, пользуются следующими правилами:

1. Погрешность измерительного прибора  указывается либо в паспорте, либо непосредственно на самом приборе. Например, на микрометре указана погрешность 0,01 мм, на штангенциркуле 0,05 или 0,1 мм.

2. Если прибор имеет класс точности (его величина указывается в паспорте и (или) на шкале прибора), то приборная погрешность определяется формулой:

,                                (12.6)

где k – величина класса точности прибора;  – предел измерения прибора. Существуют девять классов точности электроизмерительных приборов: 0,02; 0,05; 0,1; 0,2; 0,5; 1,0; 0,5; 2,5; 4,0. Класс точности указан в правом нижнем углу шкалы прибора соответствующей цифрой в кружочке или в центре с указанием пределов измерения величины.

3. Если прибор не имеет класса точности, то приборная погрешность определяется половиной цены деления шкалы прибора.

Определяемая таким образом приборная погрешность показывает максимально возможное отклонение показаний прибора от «истинного» значения измеряемой величины, обусловленное случайными факторами, связанными с процедурой измерения с помощью данного прибора. Ей соответствует значение доверительной вероятности p =100%.

Если в процессе многократных измерений выясняется, что основной вклад в случайную погрешность вносит приборная погрешность, то в данном эксперименте можно ограничиться однократными измерениями. На практике мы чаще всего имеем дело именно с ними. В этом случае оценка «истинного» значения измеряемойвеличины будет определяться однократным показанием прибора, а оценка погрешности измерения – приборной погрешностью. Если же основной вклад определяется не приборной погрешностью, то принципиальным становится именно проведение многократных измерений. В таком случае необходимо проводить статистическую обработку результатов многократных измерений. В качестве оценки «истинного» значения при этом будет выступать величинасреднего значения, а в качестве оценки погрешности – доверительная погрешность.

    Очень часто при вычислении приходится пользоваться физическими величинами, взятыми из справочников и таблиц, например, число π, ускорения свободного падения g и т.д. Их погрешность принимается равной половине единицы последнего десятичного разряда, например, π=3,14±0,005; g =(9,81±0,005) м/с². При точности (числа знаков) табличных данных необходимо руководствоваться тем, чтобы их относительная погрешность по порядку величины не отличалась значительно от относительной погрешности остальных физических величин, входящих в эту же формулу.