Численное интегрирование
Вводные замечания
Пусть на отрезке [ a, b ] задана функция y = f (x). С помощью точек x 0, x 1 ,…, x n разобьем отрезок [ a, b ] на n элементарных отрезков [xi-1, x i] (i = 1, 2 ,…, n), причем x 0 =а, x n = b. На каждом из этих элементарных отрезков выберем произвольную точку  . Найдем произведение S i значения функции в этой точке f (ξ i) на длину элементарного отрезка
. Найдем произведение S i значения функции в этой точке f (ξ i) на длину элементарного отрезка  :
:
 . (6.1)
. (6.1)
Составим сумму таких произведений
 . (6.2)
. (6.2)
Сумма S называется интегральной суммой. Определенным интегралом от функции f (x) на отрезке [ a, b ] называется предел интегральной суммы при неограниченном увеличении числа точек разбиения [13, 20]. При этом длина наибольшего из элементарных отрезков стремится к нулю.
 . (6.3)
. (6.3)
Если функция f (x) непрерывна на отрезке [ a, b ], то предел интегральной суммы существует и не зависит ни от способа разбиения отрезка [ a, b ] на
элементарные отрезки, ни от выбора точек ξi.
Геометрический смысл введенных понятий для случая  проиллюстрирован на рис. 6.1.
проиллюстрирован на рис. 6.1.
Абсциссами точек М iявляются значения ξi, ординатами – значения f (ξ i). Формула (6.1) при i = 1,2,…, n описывает площади элементарных прямоугольников (штриховые линии). Интегральная сумма (6.2) – площадь ступенчатой фигуры, образуемой этими прямоугольниками. При неограниченном увеличении числа точек деления и стремлении к нулю всех элементов  верхняя граница фигуры (ломаная) переходит в линию y = f (x). Площадь полученной
верхняя граница фигуры (ломаная) переходит в линию y = f (x). Площадь полученной

Рис. 6.1. Геометрический смысл определенного интеграла
фигуры, которую называют криволинейной трапецией, равна определенному интегралу (6.3).
Если подынтегральная функция задана в аналитическом виде, определенный интеграл равен приращению первообразной F (x) на отрезке интегрирования
 . (6.4)
. (6.4)
Например, если f (x) = x 2, то
 .
.
На практике формулой (6.4) часто нельзя воспользоваться по двум причинам:
1) вид функции f (x) не допускает непосредственного интегрирования, т.е. первообразную нельзя выразить в элементарных функциях (говорят, что
интеграл не берущийся; он не сводится к стандартному).
2) значения функции f (x) заданы только на фиксированном конечном множестве точек x i, т.е. функция задана в виде таблицы.
В обоих случаях используются методы численного интегрирования. Они основаны на аппроксимации (приближении) подынтегральной функции некоторым более простым выражением, например интерполяционными многочленами.
В дальнейшем будем использовать кусочную (локальную) интерполяцию. Это позволит приближенно заменить определенный интеграл интегральной суммой (6.2). В зависимости от способа вычисления этой суммы получаются разные формулы численного интегрирования: методы прямоугольников, трапеций, парабол и др.
К вычислению определенного интеграла сводятся многие практические задачи: вычисление площади фигур, определение работы переменной силы и т.д.
Пример использования методов прямоугольников и трапеций
Вычислим интеграл  . Это табличный интеграл и он вычисляется точно:
. Это табличный интеграл и он вычисляется точно:

Используем теперь формулы прямоугольников и трапеций. Разобьем отрезок интегрирования [0, 1] на десять равных частей: n = 10. Тогда шаг интегрирования h = 0,1 ( ). Вычислим значения подынтегральной функции
). Вычислим значения подынтегральной функции  в точках разбиения xi = xi - 1 + h, а также в средних точках элементарных отрезков
в точках разбиения xi = xi - 1 + h, а также в средних точках элементарных отрезков  (i = 1, 2, …, 10). Результаты сведены в табл. 6.1.
(i = 1, 2, …, 10). Результаты сведены в табл. 6.1.
Таблица 6.1
Результаты промежуточных вычислений при численном интегрировании
| xi
| yi
| 
| 
|
| 0,0
| 1,000000
|
|
|
| 0,1
| 0,99099
| 0,05
| 0,997506
|
| 0,2
| 0,961538
| 0,15
| 0,977995
|
| …
| …
| …
| …
|
| 0,9
| 0,552486
| 0,85
| 0,580552
|
| 1,0
| 0,500000
| 0,95
| 0,525624
|
Значение интеграла по формуле прямоугольников:

Значение интеграла по формуле трапеций:

Погрешность вычислений по формуле прямоугольников:
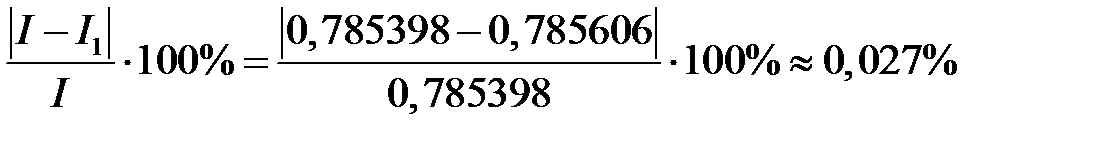 .
.
Погрешность вычислений по формуле трапеций:

Отметим, что формула трапеций по сравнению с формулой прямоугольника может дать и более точный результат. Это зависит от вида подынтегральной функции.
Уменьшая шаг разбиения можно добиться большей точности численного
интегрирования. Однако увеличить число точек не всегда возможно. Если функция задана в табличном виде (она является результатом экспериментов), то приходится ограничиваться данным множеством точек. Повышение точности в этом случае может быть достигнуто за счет повышения степени используемых интерполяционных многочленов. Например, использование квадратичной интерполяции приводит к методу Симпсона [18, 20].
Пример вычисления двойного интеграла методом ячеек
Вычислить интеграл
 . (6.20)
. (6.20)
Здесь подынтегральная функция  ;
;  ;
;  ;
; 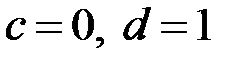 ;
;  .
.
Примем количество элементарных отрезков на осях х и у соответственно m = 4, n = 4(количество узловых точек m + 1 = 5 и n + 1 = 5). Тогда размеры ячеек:

 .
.
Количество ячеек m ∙ n = 4∙4= 16. Расчетная схема представлена на рис. 6.4. Внутри ячеек проставлены их порядковые номера. Координаты узловых точек: x 0 = 1,0; x 1 = 1,5;…; x 4 = 3; y 0 = 0; y 1 = 0,25;…; y 4 = 1,0.
Вычисление интеграла (6.20) выполняем непосредственно по формуле (6.18) с учетом того, что размеры всех ячеек одинаковы, т.е.  и
и
 :
:

Рис. 6.4. Расчетная схема к вычислению интеграла (6.20)

Пример вычисления двойного интеграла методом последовательного вычисления определенных интегралов
Вычислим интеграл (6.20) с использованием формул (6.19). Количество элементарных отрезков и, следовательно, размеры ячеек  ,
, 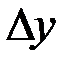 и координаты узловых точек такие же, как и в примере, рассмотренном в разделе 6.6.
и координаты узловых точек такие же, как и в примере, рассмотренном в разделе 6.6.
Для вычисления определенных интегралов, входящих в (6.19), будем использовать формулу трапеций (6.12). Запишем эту формулу применительно к вычислению значения  (второе выражение в (6.19)) при фиксированном значении х:
(второе выражение в (6.19)) при фиксированном значении х:
 . (6.21)
. (6.21)
Формулу (6.21) последовательно применим для вычисления  при х i = 1,0; 1,5; 2,0; 2,5; 3,0:
при х i = 1,0; 1,5; 2,0; 2,5; 3,0:


 ;
;  ;
;  .
.
Здесь вычисления подынтегральной функции производились по формуле
 . Например, при х = 1,5 и у = 0,25
. Например, при х = 1,5 и у = 0,25 
 .
.
Формулу трапеций (6.12) применительно к вычислению двойного интеграла I (первое выражение в (6.19)) запишем следующим образом:
 (6.22)
(6.22)
Подставляя ранее вычисленные значения  в выражение (6.22), получим
в выражение (6.22), получим
 .
.
При вычислении по формуле ячеек этого же интеграла в разделе 6.6 ранее получили I = 10,218. Таким образом, относительное отклонение составляет:
 .
.
Отметим, что вычисление двойного интеграла методом последовательного вычисления определенных интегралов по сравнению с методом ячеек требует большего количества вычислений.
Методика расчета
Рассмотрим с использованием энергетического метода осадку кольцевой заготовки в контейнере (рис. 6.5) [6, 12]. Особенность такой осесимметричной схемы деформации состоит в том, что течение металла в радиальном направлении может происходить только в сторону оси симметрии заготовки (оси z). Течению металла от оси z будет препятствовать поверхность контейнера.
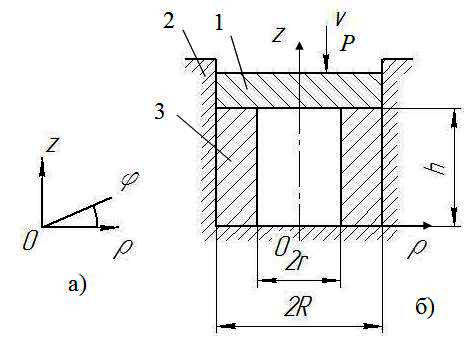
Рис. 6.5. Осадка кольцевой заготовки в контейнере:
а – цилиндрическая система координат; б – схема деформирования; 1 – верхний боек; 2 – контейнер; 3 – заготовка; 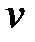 - скорость перемещения бойка; Р – сила осадки
- скорость перемещения бойка; Р – сила осадки
Осадка является нестационарным процессом деформации, т.е. в каждый момент времени 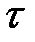 изменяются скорости перемещения
изменяются скорости перемещения 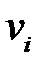 , скорости деформации
, скорости деформации 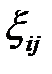 (
(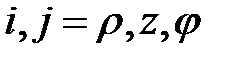 ), размеры очага деформации (высота h и внутренний диаметр 2 r). Наружный диаметр (2 R) остаётся неизменным. Осадка может происходить до тех пор, пока металл не заполнит полностью внутреннюю полость кольца.
), размеры очага деформации (высота h и внутренний диаметр 2 r). Наружный диаметр (2 R) остаётся неизменным. Осадка может происходить до тех пор, пока металл не заполнит полностью внутреннюю полость кольца.
Осадка является осесимметричной деформацией. Поэтому скорости перемещения 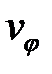 = 0,
= 0, 
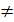 0,
0, 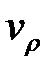
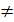 0. Причем скорости
0. Причем скорости  и
и 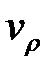 от координаты
от координаты 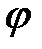 не зависят. При определении
не зависят. При определении 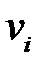 и
и 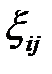 используем общепринятое допущение энергетического метода: скорости линейных деформаций
используем общепринятое допущение энергетического метода: скорости линейных деформаций 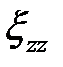 ,
, 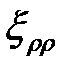 и
и 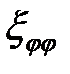 от координат
от координат 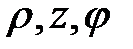 не зависят.
не зависят.
Определим кинематически возможное поле скоростей. Эти скорости 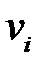 и
и 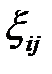 удовлетворяющие граничным условиям (ГУ) в скоростях и условию несжимаемости. Выводы следует начинать с определения скоростей, совпадающих с направлением перемещения инструмента:
удовлетворяющие граничным условиям (ГУ) в скоростях и условию несжимаемости. Выводы следует начинать с определения скоростей, совпадающих с направлением перемещения инструмента: 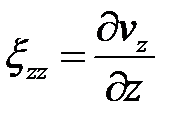 ;
; 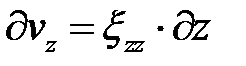 . Интегрируем:
. Интегрируем: 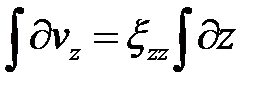 ,
, 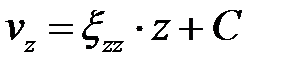 . Константу интегрирования С находим из ГУ:
. Константу интегрирования С находим из ГУ:
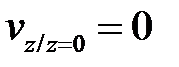 . Получаем С = 0 и, следовательно,
. Получаем С = 0 и, следовательно,  ,
, 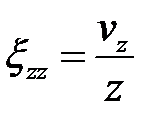 . Используем второе ГУ:
. Используем второе ГУ: 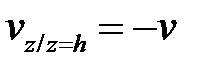 . Получаем
. Получаем
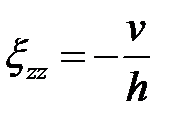 ,
, 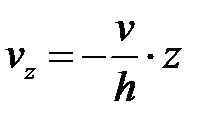 . (6.23)
. (6.23)
По формуле (6.23) 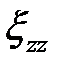 определяется в любой точке заготовки, так как скорости деформации не зависит от координат.
определяется в любой точке заготовки, так как скорости деформации не зависит от координат.
Из условия несжимаемости находим 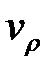 :
:
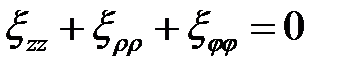 ,
, 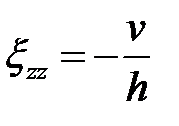 ;
; 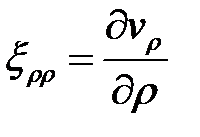 ;
; 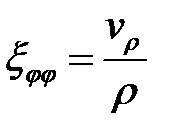 ;
;
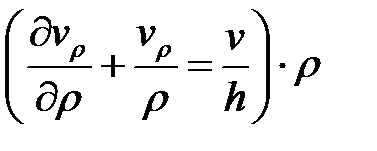 ,
, 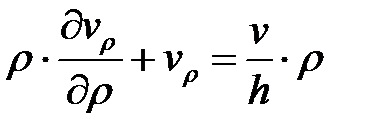 ,
, 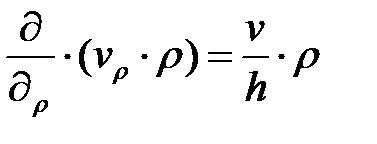 .
.
Умножаем последнее выражение на 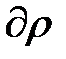 и интегрируем. Получаем:
и интегрируем. Получаем:
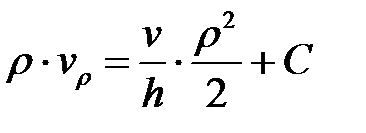 . (6.24)
. (6.24)
Константу интегрирования С находим из ГУ: 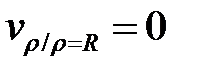 . Тогда из (6.24) следует, что
. Тогда из (6.24) следует, что 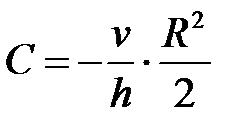 . Это С подставляем в (6.24) и получаем формулу
. Это С подставляем в (6.24) и получаем формулу
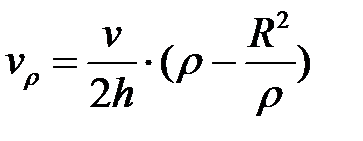 . (6.25)
. (6.25)
Скорости деформации
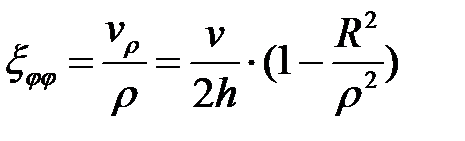 ,
,  . (6.26)
. (6.26)
Условие несжимаемости выполняется, так как сумма 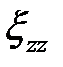 ,
, 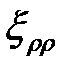 и
и 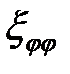 даёт 0. При осесимметричной схеме деформирования с учетом принятых допущений
даёт 0. При осесимметричной схеме деформирования с учетом принятых допущений
скорости сдвиговых деформаций 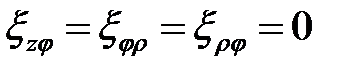 .
.
При осадке одним подвижным бойком имеем следующие выражения для расчета мощностей [1, 6]:
 ;
; 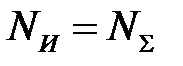 ;
; 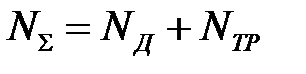 , (6.27)
, (6.27)
где 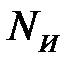 - мощность, подводимая инструментом (верхним бойком);
- мощность, подводимая инструментом (верхним бойком); 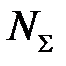 - полная (суммарная) мощность, требуемая для формоизменения заготовки;
- полная (суммарная) мощность, требуемая для формоизменения заготовки; 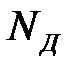 - мощность пластической деформации;
- мощность пластической деформации; 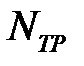 - мощность трения;
- мощность трения;
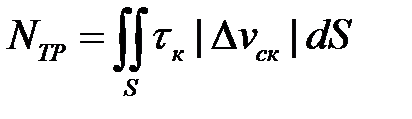 ;
; 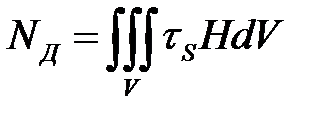 ; (6.28)
; (6.28)
V – объём заготовки; 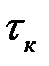 - напряжения контактного трения,
- напряжения контактного трения, 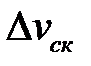 - скорость скольжения металла по контактной поверхности,
- скорость скольжения металла по контактной поверхности, 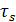 - предел текучести металла при чистом сдвиге, H – интенсивность скоростей деформаций сдвига; S – площадь контактной поверхности.
- предел текучести металла при чистом сдвиге, H – интенсивность скоростей деформаций сдвига; S – площадь контактной поверхности.
При записи выражений (6.27) и (6.28) использованы следующие допущения: 1) об идеальной пластичности металла заготовки; 2) на всей контактной поверхности реализуется только скольжение металла по поверхности инструмента (зоны прилипания отсутствуют).
Рассчитаем интенсивность скоростей деформаций сдвига H при условии, что 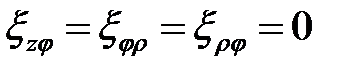 , а скорости линейных деформаций вычисляются по формулам (6.23) и (6.26):
, а скорости линейных деформаций вычисляются по формулам (6.23) и (6.26):
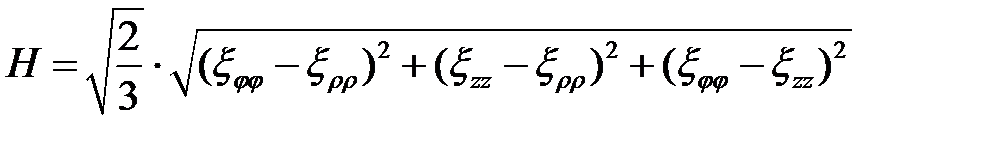 ;
;
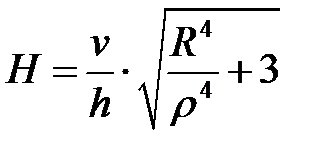 . (6.29)
. (6.29)
При вычислении мощности пластической деформации 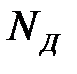 (см. (6.28)) учтем, что
(см. (6.28)) учтем, что  и
и 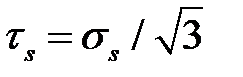 :
:
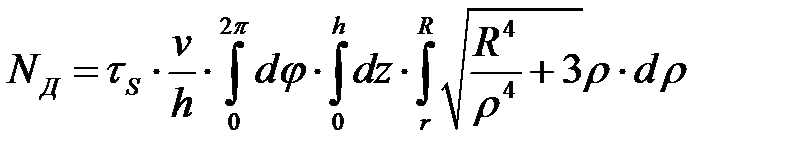 ,
,
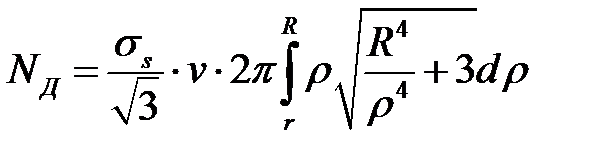 , (6.30)
, (6.30)
где 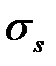 - сопротивление металла деформации. Интеграл, входящий в выражение (6.31), будем вычислять численно с заданной точностью по формуле трапеций (см. раздел 6.3).
- сопротивление металла деформации. Интеграл, входящий в выражение (6.31), будем вычислять численно с заданной точностью по формуле трапеций (см. раздел 6.3).
При вычислении мощности трения 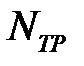 (см. (6.28)) учтем, что по закону трения Зибеля при осесимметричной деформации
(см. (6.28)) учтем, что по закону трения Зибеля при осесимметричной деформации 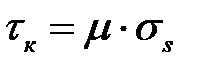 ;
; 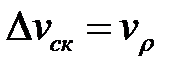 (см. (6.25));
(см. (6.25)); 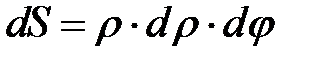 . Учтем также, что имеем две контактные поверхности (на верхнем и нижнем торцах заготовки). Тогда
. Учтем также, что имеем две контактные поверхности (на верхнем и нижнем торцах заготовки). Тогда
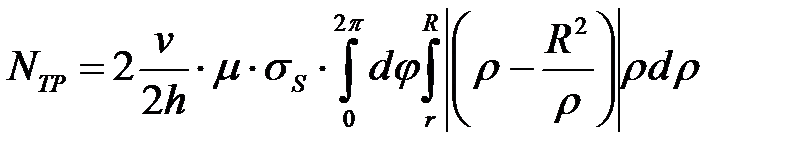 ,
,
 . (6.31)
. (6.31)
После расчета мощностей 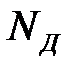 и
и 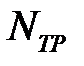 соответственно по формулам (6.30) и (6.31) вычисляем полную мощность
соответственно по формулам (6.30) и (6.31) вычисляем полную мощность 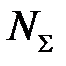 (см. (6.27)), силу Р, площадь контактной поверхности S и среднее давление р при осадке кольцевой заготовки в контейнере:
(см. (6.27)), силу Р, площадь контактной поверхности S и среднее давление р при осадке кольцевой заготовки в контейнере:
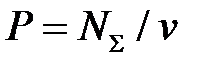 ,
, 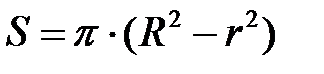 ,
, 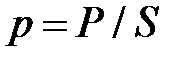 . (6.32)
. (6.32)
Для расчета сопротивления деформации 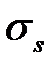 (МПа) использовали формулы [1]:
(МПа) использовали формулы [1]:
сталь 45 - 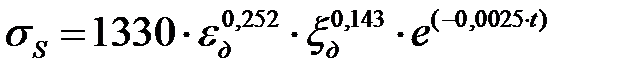 , (6.33)
, (6.33)
сталь 4Х13 -  , (6.34)
, (6.34)
где  - степень деформации;
- степень деформации; 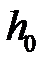 – исходная высота заготовки;
– исходная высота заготовки;  – текущая высота заготовки (на рассматриваемом этапе деформации);
– текущая высота заготовки (на рассматриваемом этапе деформации); 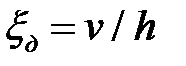 -
-
скорость деформации, 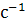 ;
; 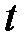 - температура металла, ˚С.
- температура металла, ˚С.
При выполнении вычислений по формулам (6.30) – (6.34) полное обжатие
заготовки 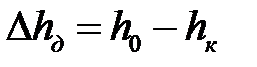 (
(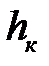 - конечная высота заготовки) разбивали на
- конечная высота заготовки) разбивали на 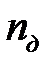 малых участков (этапов). Обжатие на каждом i – ом этапе (
малых участков (этапов). Обжатие на каждом i – ом этапе (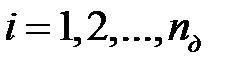 )
)  = const. Полное обжатие к концу i – го этапа
= const. Полное обжатие к концу i – го этапа 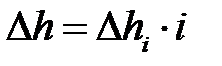 . Таким образом, в результате расчетов получим таблично заданную функцию
. Таким образом, в результате расчетов получим таблично заданную функцию 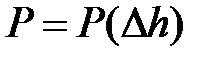 , причем при
, причем при 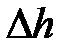 = 0 сила осадки
= 0 сила осадки 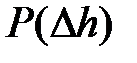 = 0.
= 0.
Полная работа деформирования при осадке заготовки
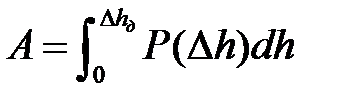 . (6.35)
. (6.35)
При численном интегрировании использовали формулу трапеций (6.12).
Методика и алгоритм расчета
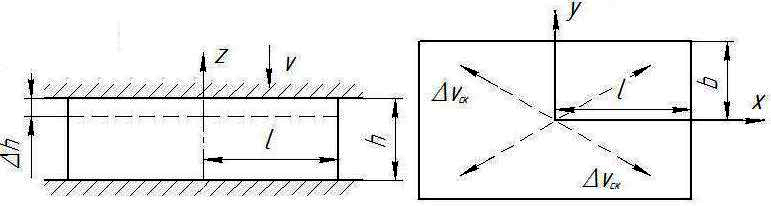
Схема осадки в прямоугольной системе координат 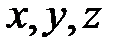 приведена на рис. 6.9. Следуя работе [1], используем следующие допущения: 1) деформация равномерная (т.е. сечения заготовки плоские до деформации остаются плоскими и после неё); 2) скорости линейных деформаций
приведена на рис. 6.9. Следуя работе [1], используем следующие допущения: 1) деформация равномерная (т.е. сечения заготовки плоские до деформации остаются плоскими и после неё); 2) скорости линейных деформаций 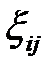 не зависят от координат (
не зависят от координат (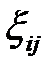 = const,
= const, 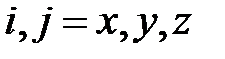 ); 3) материал заготовки жесткопластический (идеально пластический), т.е. T =
); 3) материал заготовки жесткопластический (идеально пластический), т.е. T = 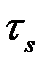 ; 4) на всей контактной поверхности реализуется скольжение (если для исходных размеров выполняется h 0 < l 0 и h 0 <10, т.е. рассматривается осадка низкого параллелепипеда).
; 4) на всей контактной поверхности реализуется скольжение (если для исходных размеров выполняется h 0 < l 0 и h 0 <10, т.е. рассматривается осадка низкого параллелепипеда).
Определим кинематически возможное поле скоростей при объемной схеме деформирования. Из допущений и граничных условий следует:
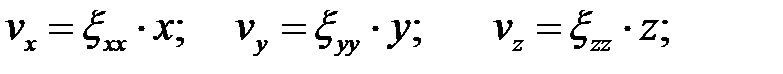
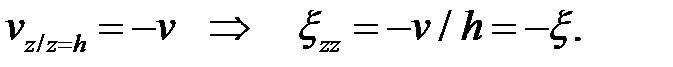
Введем обозначение: 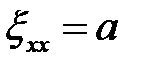 . Здесь а – варьируемый параметр, характеризующий течение металла в ширину. На данном этапе решения параметр а неизвестен.
. Здесь а – варьируемый параметр, характеризующий течение металла в ширину. На данном этапе решения параметр а неизвестен.
а) б)
Рис. 6.9. Схема осадки параллелепипеда: а – вид спереди, б – вид сверху
Скорость деформации 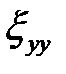 определим из условия несжимаемости:
определим из условия несжимаемости:
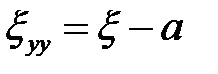 .
.
Параметр а рассчитаем из условия минимума полной мощности 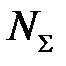 : на
: на
действительном поле скоростей 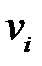 ,
, 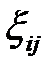 (и, следовательно, значении а) мощность
(и, следовательно, значении а) мощность 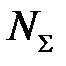 минимальна. Из этого принципа следует уравнение для определения а:
минимальна. Из этого принципа следует уравнение для определения а:
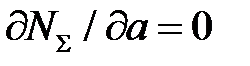 .
.
При анализе осадки параллелепипеда будем использовать формулы (6.27) и (6.28), которые следуют из баланса мощностей. Причем в прямоугольной системе координат 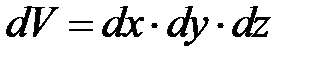 ,
, 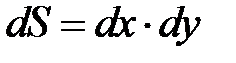 (см. рис. 6.9).
(см. рис. 6.9).
Напряжения контактного трения при объемной схеме деформирования будем определять по закону трения Зибеля - 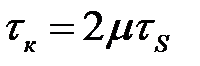 . Рассчитаем интенсивность скоростей деформаций сдвига H при условии, что
. Рассчитаем интенсивность скоростей деформаций сдвига H при условии, что 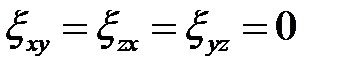 , а скорости линейных деформаций
, а скорости линейных деформаций 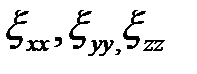 определены выше через параметры а и
определены выше через параметры а и 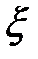 :
:
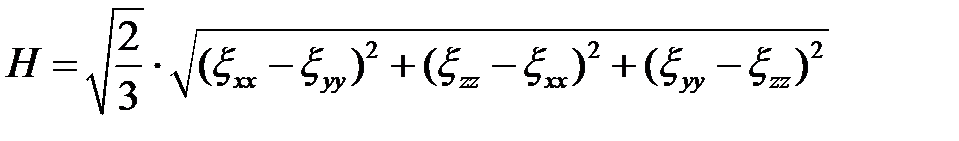 ;
;
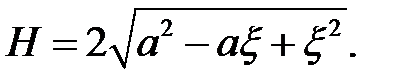 (6.36)
(6.36)
Модуль вектора скорости скольжения металла по бойкам (см. рис. 6.9 б)

Таким образом, полная мощность формоизменения
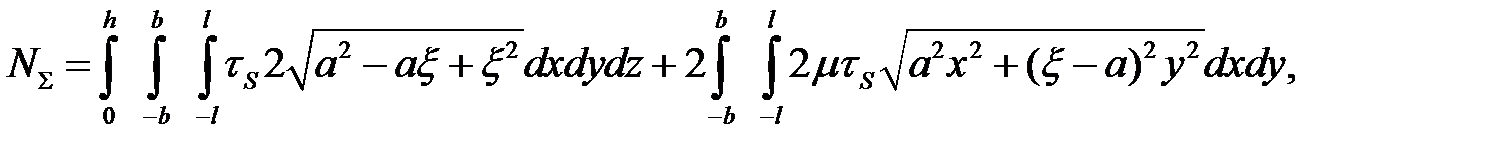
или
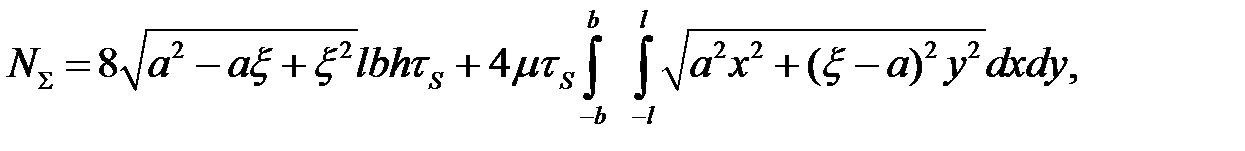 (6.37)
(6.37)
где l, b, h – размеры параллелепипеда в момент времени 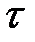 . В начальный момент времени
. В начальный момент времени 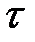 = 0 размеры соответственно равны l 0, b 0, h 0.
= 0 размеры соответственно равны l 0, b 0, h 0.
При вычислении 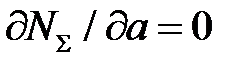 используем формулу (6.37). Получаем
используем формулу (6.37). Получаем
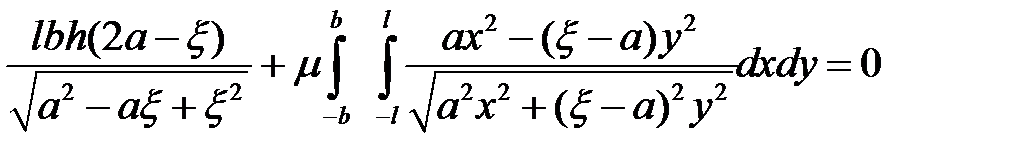 . (6.38)
. (6.38)
Для того, чтобы вычислить производную применили правило дифференцирования сложной функции 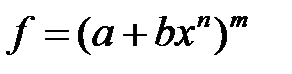 :
:
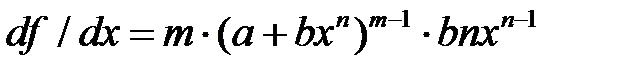 .
.
Уравнение (6.38) содержит только одну неизвестную величину а и его будем решать методом половинного деления (см. раздел 2.1.2). Для этого предполагается, что заданы размеры заготовки l, b, h; коэффициент трения 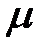 , параметр
, параметр 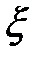 и вычислен двойной интеграл. Интеграл будем вычислять методом ячеек (см. разделы 6.5 и 6.6).
и вычислен двойной интеграл. Интеграл будем вычислять методом ячеек (см. разделы 6.5 и 6.6).
Для численного решения уравнения (6.38) необходимо задать область изменения параметра  . Известно, что средняя скорость деформации
. Известно, что средняя скорость деформации 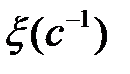 при ковке и горячей объемной штамповке изменяется в следующих пределах: гидравлические прессы – 0.03....0.06; кривошипные прессы – 1...10; молоты – 10...250 [1].
при ковке и горячей объемной штамповке изменяется в следующих пределах: гидравлические прессы – 0.03....0.06; кривошипные прессы – 1...10; молоты – 10...250 [1].
Рассмотрим кратко алгоритм расчета шаговым методом формоизменения и энергосиловых параметров при осадке параллелепипеда.
Величина а, определенная из уравнения (6.38), описывает деформированное состояние металла (скорости перемещения (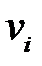 ) и деформации (
) и деформации (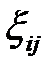 )) – в фиксированный момент времени
)) – в фиксированный момент времени 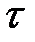 .
.
Процесс осадки является нестационарным процессом, т.е. с течением времени размеры заготовки и, следовательно, деформированное состояние металла изменяются. Поэтому расчет формоизменения (размеров заготовки) и энергосиловых параметров (усилия Р и давления р) при осадке заготовки на величину полного обжатия 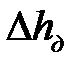 необходимо выполнять шаговым методом. Для этого полное обжатие
необходимо выполнять шаговым методом. Для этого полное обжатие 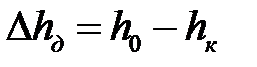 разбивали на этапы (шаги) так, чтобы на каждом из них заданная относительная деформация
разбивали на этапы (шаги) так, чтобы на каждом из них заданная относительная деформация 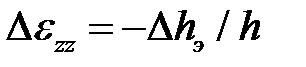 была достаточно мала:
была достаточно мала: 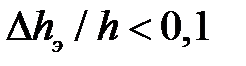 . Здесь
. Здесь 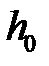 и
и 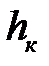 - соответственно начальная и конечная высота заготовки;
- соответственно начальная и конечная высота заготовки; 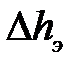 - обжатие на i – ом этапе;
- обжатие на i – ом этапе; 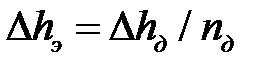 = const;
= const; 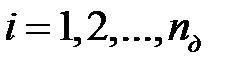 ;
; 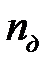 - количество этапов;
- количество этапов; 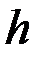 - высота заготовки на этапе;
- высота заготовки на этапе;  .
.
В пределах шага можно считать, что 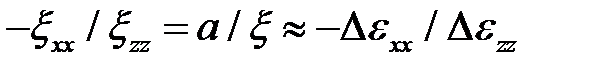 , где
, где 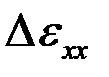 и
и 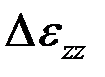 – приращения деформаций. Зная исходные размеры
– приращения деформаций. Зная исходные размеры
параллелепипеда l 0, b 0, h 0, после решения уравнения (6.38) можно определить:
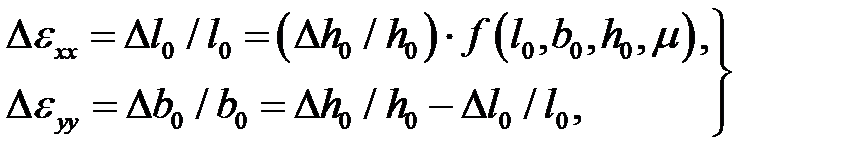 (6.39)
(6.39)
где в правой части верхнего равенства содержится известная функция  при l=l0, b=b0, h=h0,
при l=l0, b=b0, h=h0, 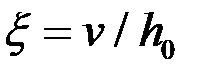 . Затем подсчитывают абсолютную деформацию
. Затем подсчитывают абсолютную деформацию 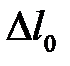 и
и 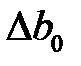 , а также размеры параллелепипеда к началу следующего шага
, а также размеры параллелепипеда к началу следующего шага
 ,
, 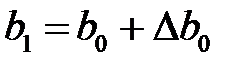 ,
, 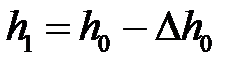 (
(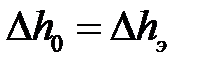 ). (6.40)
). (6.40)
Аналогично определяют 
 На этом шаге
На этом шаге 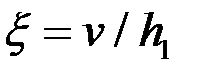 . Затем следует третий шаг и т. д. В итоге решаем задачу расчета формоизменения параллелепипеда.
. Затем следует третий шаг и т. д. В итоге решаем задачу расчета формоизменения параллелепипеда.
На каждом шаге решения определяли силу деформирования и давление
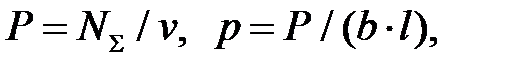 (6.41)
(6.41)
где полная мощность 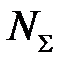 определяется по формуле (6.37).
определяется по формуле (6.37).
Таким образом, численный расчет параметров осадки низкого параллелепипеда реализуется следующим алгоритмом.
1. Ввести исходные данные: l0, b0, h0 (h0 < b0, h0 < l 0), v, µ, t, h к, ε, an, a к, n, m _ stal (ε – заданная точность решения уравнения (6.38); an и a к – пределы изменения параметра а при решении уравнения (6.38); n - количество малых отрезков разбиения по осям x и y при вычислении интегралов в выражениях (6.37) и (6.38); m _ stal – код марки стали при вычислении сопротивления деформации по формулам (6.33) и (6.34)).
2. Рассчитать 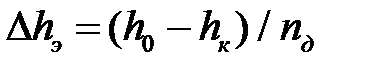 ; принять
; принять 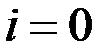 ;
; 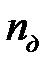 = 10.
= 10.
3. Принять h = h i, b = b i, l = l i, 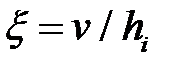 и из уравнения (6.38) определить параметр а.
и из уравнения (6.38) определить параметр а.
4. Принять i = i + 1.
5. Вычислить 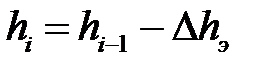 . По известному а и формулам (6.39), (6.40)
. По известному а и формулам (6.39), (6.40)
определить li, bi. Рассчитать 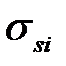 по формуле (6.33) или (6.34) (в зависимости от заданной марки стали); суммарную мощность
по формуле (6.33) или (6.34) (в зависимости от заданной марки стали); суммарную мощность 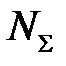 по (6.37); силу Pi и давление pi по формулам (6.41).
по (6.37); силу Pi и давление pi по формулам (6.41).
6. Печатать а, l i, b i, h i, σ si, Pi, pi.
7. Если i < 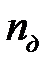 идти к к пункту 3.
идти к к пункту 3.
Численное интегрирование
Вводные замечания
Пусть на отрезке [ a, b ] задана функция y = f (x). С помощью точек x 0, x 1 ,…, x n разобьем отрезок [ a, b ] на n элементарных отрезков [xi-1, x i] (i = 1, 2 ,…, n), причем x 0 =а, x n = b. На каждом из этих элементарных отрезков выберем произвольную точку  . Найдем произведение S i значения функции в этой точке f (ξ i) на длину элементарного отрезка
. Найдем произведение S i значения функции в этой точке f (ξ i) на длину элементарного отрезка  :
:
 . (6.1)
. (6.1)
Составим сумму таких произведений
 . (6.2)
. (6.2)
Сумма S называется интегральной суммой. Определенным интегралом от функции f (x) на отрезке [ a, b ] называется предел интегральной суммы при неограниченном увеличении числа точек разбиения [13, 20]. При этом длина наибольшего из элементарных отрезков стремится к нулю.
 . (6.3)
. (6.3)
Если функция f (x) непрерывна на отрезке [ a, b ], то предел интегральной суммы существует и не зависит ни от способа разбиения отрезка [ a, b ] на
элементарные отрезки, ни от выбора точек ξi.
Геометрический смысл введенных понятий для случая  проиллюстрирован на рис. 6.1.
проиллюстрирован на рис. 6.1.
Абсциссами точек М iявляются значения ξi, ординатами – значения f (ξ i). Формула (6.1) при i = 1,2,…, n описывает площади элементарных прямоугольников (штриховые линии). Интегральная сумма (6.2) – площадь ступенчатой фигуры, образуемой этими прямоугольниками. При неограниченном увеличении числа точек деления и стремлении к нулю всех элементов  верхняя граница фигуры (ломаная) переходит в линию y = f (x). Площадь полученной
верхняя граница фигуры (ломаная) переходит в линию y = f (x). Площадь полученной

Рис. 6.1. Геометрический смысл определенного интеграла
фигуры, которую называют криволинейной трапецией, равна определенному интегралу (6.3).
Если подынтегральная функция задана в аналитическом виде, определенный интеграл равен приращению первообразной F (x) на отрезке интегрирования
 . (6.4)
. (6.4)
Например, если f (x) = x 2, то
 .
.
На практике формулой (6.4) часто нельзя воспользоваться по двум причинам:
1) вид функции f (x) не допускает непосредственного интегрирования, т.е. первообразную нельзя выразить в элементарных функциях (говорят, что
интеграл не берущийся; он не сводится к стандартному).
2) значения функции f (x) заданы только на фиксированном конечном множестве точек x i, т.е. функция задана в виде таблицы.
В обоих случаях используются методы численного интегрирования. Они основаны на аппроксимации (приближении) подынтегральной функции некоторым более простым выражением, например интерполяционными многочленами.
В дальнейшем будем использовать кусочную (локальную) интерполяцию. Это позволит приближенно заменить определенный интеграл интегральной суммой (6.2). В зависимости от способа вычисления этой суммы получаются разные формулы численного интегрирования: методы прямоугольников, трапеций, парабол и др.
К вычислению определенного интеграла сводятся многие практические задачи: вычисление площади фигур, определение работы переменной силы и т.д.
Методы прямоугольников и трапеций
Простейшим методом численного интегрирования является метод прямоугольников [7, 18]. Он непосредственно использует замену определенного интеграла интегральной суммой
 ; (6.5)
; (6.5)
 . (6.6)
. (6.6)
В качестве точек ξ i выберем средние точки элементарных отрезков [ xi - 1, xi ]. Введем обозначения:
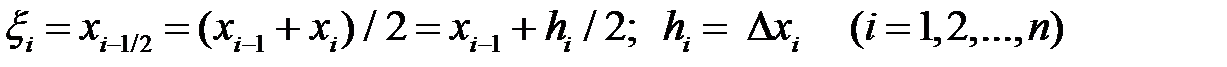 . (6.7)
. (6.7)
Напомним, что  .
.
Тогда с учетом (6.5), (6.6) и (6,7) можно записать:
 ; i = 1, 2 ,…, n. (6.8)
; i = 1, 2 ,…, n. (6.8)
Формула (6.8) и есть формула прямоугольников. Эта формула использует интерполяцию нулевого порядка (кусочно постоянную, т.е. на элементарном отрезке график подынтегральной функции заменяется горизонтальным отрезком; см. рис. 6.1).
Метод трапеций использует линейную интерполяцию, т.е. график функции y = f (x) представляется в виде ломанной, соединяющей точки с координатами (xi - 1, yi - 1) и (xi, yi). В этом случае площадь всей фигуры (криволинейной трапеции) складывается из площадей элементарных прямолинейных трапеций (рис. 6.2).

Рис. 6.2. Схема к выводу формулы трапеций
Площадь каждой элементарной трапеции равна произведению полусуммы оснований на высоту:
 ; (i = 1, 2, …, n). (6.9)
; (i = 1, 2, …, n). (6.9)
Суммируя площади элементарных фигур, получае



 . Найдем произведение S i значения функции в этой точке f (ξ i) на длину элементарного отрезка
. Найдем произведение S i значения функции в этой точке f (ξ i) на длину элементарного отрезка  :
: . (6.1)
. (6.1) . (6.2)
. (6.2) . (6.3)
. (6.3) проиллюстрирован на рис. 6.1.
проиллюстрирован на рис. 6.1. верхняя граница фигуры (ломаная) переходит в линию y = f (x). Площадь полученной
верхняя граница фигуры (ломаная) переходит в линию y = f (x). Площадь полученной
 . (6.4)
. (6.4) .
. . Это табличный интеграл и он вычисляется точно:
. Это табличный интеграл и он вычисляется точно:
 ). Вычислим значения подынтегральной функции
). Вычислим значения подынтегральной функции  в точках разбиения xi = xi - 1 + h, а также в средних точках элементарных отрезков
в точках разбиения xi = xi - 1 + h, а также в средних точках элементарных отрезков  (i = 1, 2, …, 10). Результаты сведены в табл. 6.1.
(i = 1, 2, …, 10). Результаты сведены в табл. 6.1.



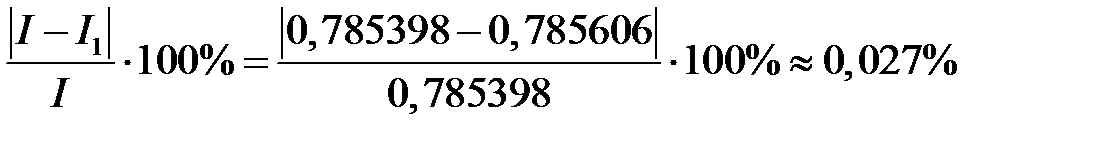 .
.
 . (6.20)
. (6.20) ;
;  ;
;  ;
; 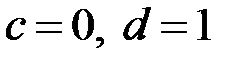 ;
;  .
.
 .
. и
и :
:

 ,
, 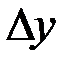 и координаты узловых точек такие же, как и в примере, рассмотренном в разделе 6.6.
и координаты узловых точек такие же, как и в примере, рассмотренном в разделе 6.6. (второе выражение в (6.19)) при фиксированном значении х:
(второе выражение в (6.19)) при фиксированном значении х: . (6.21)
. (6.21)

 ;
;  ;
;  .
.
 .
. (6.22)
(6.22) .
. .
.
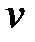 - скорость перемещения бойка; Р – сила осадки
- скорость перемещения бойка; Р – сила осадки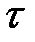 изменяются скорости перемещения
изменяются скорости перемещения 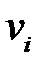 , скорости деформации
, скорости деформации 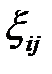 (
(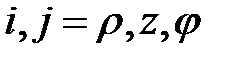 ), размеры очага деформации (высота h и внутренний диаметр 2 r). Наружный диаметр (2 R) остаётся неизменным. Осадка может происходить до тех пор, пока металл не заполнит полностью внутреннюю полость кольца.
), размеры очага деформации (высота h и внутренний диаметр 2 r). Наружный диаметр (2 R) остаётся неизменным. Осадка может происходить до тех пор, пока металл не заполнит полностью внутреннюю полость кольца.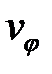 = 0,
= 0, 
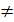 0,
0, 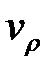
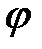 не зависят. При определении
не зависят. При определении 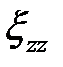 ,
, 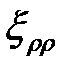 и
и 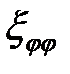 от координат
от координат 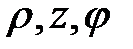 не зависят.
не зависят.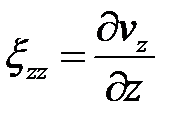 ;
; 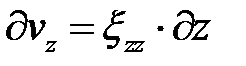 . Интегрируем:
. Интегрируем: 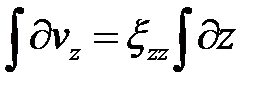 ,
, 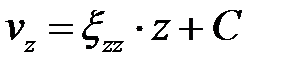 . Константу интегрирования С находим из ГУ:
. Константу интегрирования С находим из ГУ: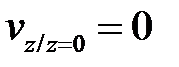 . Получаем С = 0 и, следовательно,
. Получаем С = 0 и, следовательно,  ,
, 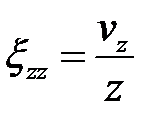 . Используем второе ГУ:
. Используем второе ГУ: 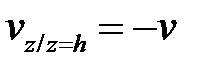 . Получаем
. Получаем 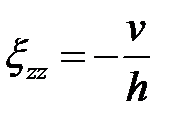 ,
, 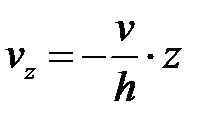 . (6.23)
. (6.23)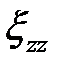 определяется в любой точке заготовки, так как скорости деформации не зависит от координат.
определяется в любой точке заготовки, так как скорости деформации не зависит от координат.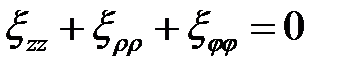 ,
, 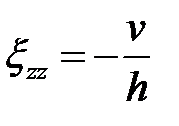 ;
; 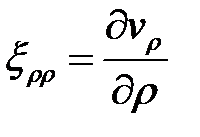 ;
; 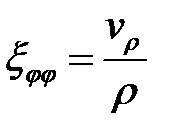 ;
;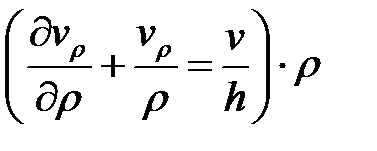 ,
, 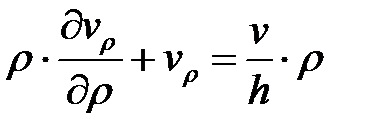 ,
, 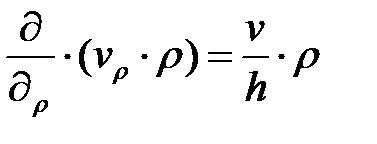 .
.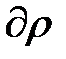 и интегрируем. Получаем:
и интегрируем. Получаем: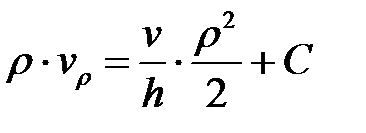 . (6.24)
. (6.24)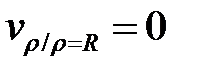 . Тогда из (6.24) следует, что
. Тогда из (6.24) следует, что 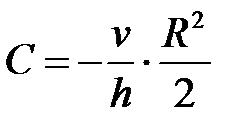 . Это С подставляем в (6.24) и получаем формулу
. Это С подставляем в (6.24) и получаем формулу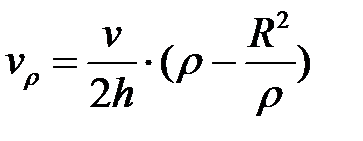 . (6.25)
. (6.25)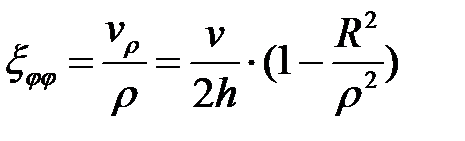 ,
,  . (6.26)
. (6.26)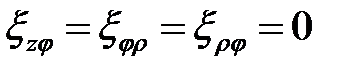 .
. ;
; 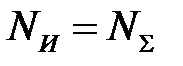 ;
; 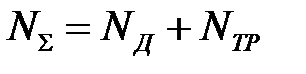 , (6.27)
, (6.27)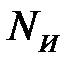 - мощность, подводимая инструментом (верхним бойком);
- мощность, подводимая инструментом (верхним бойком); 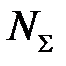 - полная (суммарная) мощность, требуемая для формоизменения заготовки;
- полная (суммарная) мощность, требуемая для формоизменения заготовки; 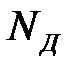 - мощность пластической деформации;
- мощность пластической деформации; 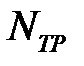 - мощность трения;
- мощность трения;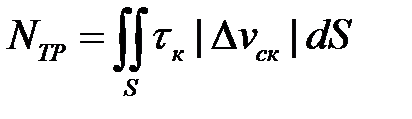 ;
; 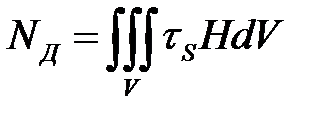 ; (6.28)
; (6.28)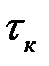 - напряжения контактного трения,
- напряжения контактного трения, 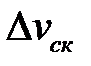 - скорость скольжения металла по контактной поверхности,
- скорость скольжения металла по контактной поверхности, 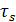 - предел текучести металла при чистом сдвиге, H – интенсивность скоростей деформаций сдвига; S – площадь контактной поверхности.
- предел текучести металла при чистом сдвиге, H – интенсивность скоростей деформаций сдвига; S – площадь контактной поверхности.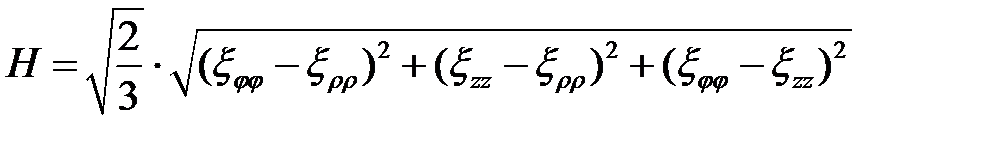 ;
;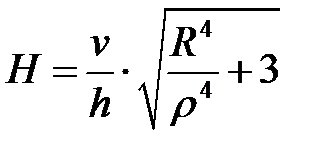 . (6.29)
. (6.29)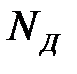 (см. (6.28)) учтем, что
(см. (6.28)) учтем, что  и
и 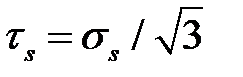 :
: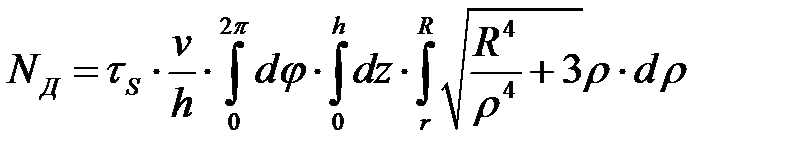 ,
,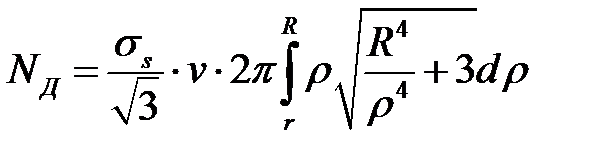 , (6.30)
, (6.30)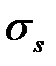 - сопротивление металла деформации. Интеграл, входящий в выражение (6.31), будем вычислять численно с заданной точностью по формуле трапеций (см. раздел 6.3).
- сопротивление металла деформации. Интеграл, входящий в выражение (6.31), будем вычислять численно с заданной точностью по формуле трапеций (см. раздел 6.3).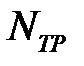 (см. (6.28)) учтем, что по закону трения Зибеля при осесимметричной деформации
(см. (6.28)) учтем, что по закону трения Зибеля при осесимметричной деформации 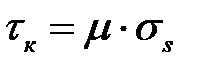 ;
; 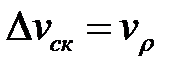 (см. (6.25));
(см. (6.25)); 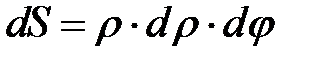 . Учтем также, что имеем две контактные поверхности (на верхнем и нижнем торцах заготовки). Тогда
. Учтем также, что имеем две контактные поверхности (на верхнем и нижнем торцах заготовки). Тогда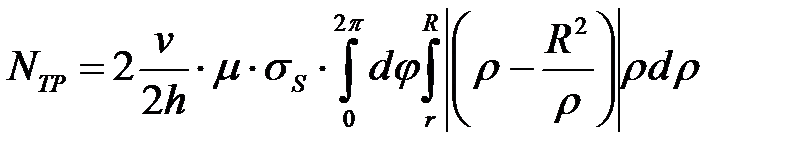 ,
, . (6.31)
. (6.31)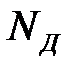 и
и 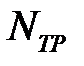 соответственно по формулам (6.30) и (6.31) вычисляем полную мощность
соответственно по формулам (6.30) и (6.31) вычисляем полную мощность 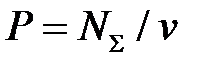 ,
, 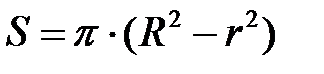 ,
, 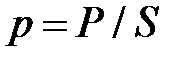 . (6.32)
. (6.32)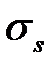 (МПа) использовали формулы [1]:
(МПа) использовали формулы [1]: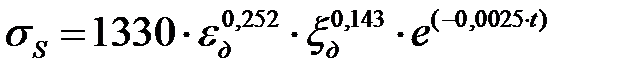 , (6.33)
, (6.33) , (6.34)
, (6.34) - степень деформации;
- степень деформации; 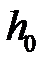 – исходная высота заготовки;
– исходная высота заготовки;  – текущая высота заготовки (на рассматриваемом этапе деформации);
– текущая высота заготовки (на рассматриваемом этапе деформации); 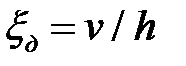 -
-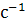 ;
; 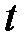 - температура металла, ˚С.
- температура металла, ˚С.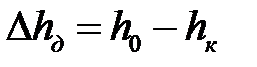 (
(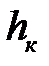 - конечная высота заготовки) разбивали на
- конечная высота заготовки) разбивали на 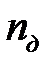 малых участков (этапов). Обжатие на каждом i – ом этапе (
малых участков (этапов). Обжатие на каждом i – ом этапе (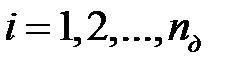 )
)  = const. Полное обжатие к концу i – го этапа
= const. Полное обжатие к концу i – го этапа 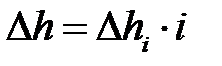 . Таким образом, в результате расчетов получим таблично заданную функцию
. Таким образом, в результате расчетов получим таблично заданную функцию 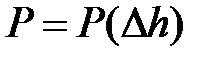 , причем при
, причем при 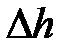 = 0 сила осадки
= 0 сила осадки 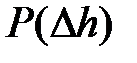 = 0.
= 0.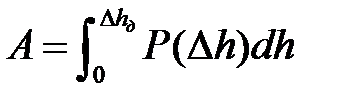 . (6.35)
. (6.35)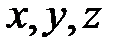 приведена на рис. 6.9. Следуя работе [1], используем следующие допущения: 1) деформация равномерная (т.е. сечения заготовки плоские до деформации остаются плоскими и после неё); 2) скорости линейных деформаций
приведена на рис. 6.9. Следуя работе [1], используем следующие допущения: 1) деформация равномерная (т.е. сечения заготовки плоские до деформации остаются плоскими и после неё); 2) скорости линейных деформаций 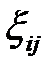 не зависят от координат (
не зависят от координат (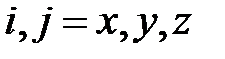 ); 3) материал заготовки жесткопластический (идеально пластический), т.е. T =
); 3) материал заготовки жесткопластический (идеально пластический), т.е. T = 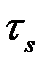 ; 4) на всей контактной поверхности реализуется скольжение (если для исходных размеров выполняется h 0 < l 0 и h 0 <10, т.е. рассматривается осадка низкого параллелепипеда).
; 4) на всей контактной поверхности реализуется скольжение (если для исходных размеров выполняется h 0 < l 0 и h 0 <10, т.е. рассматривается осадка низкого параллелепипеда).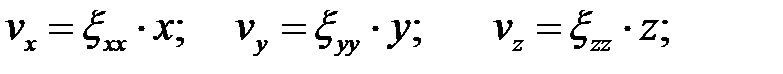
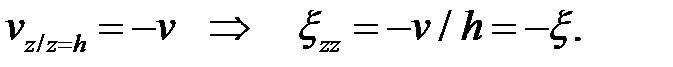
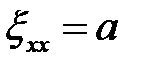 . Здесь а – варьируемый параметр, характеризующий течение металла в ширину. На данном этапе решения параметр а неизвестен.
. Здесь а – варьируемый параметр, характеризующий течение металла в ширину. На данном этапе решения параметр а неизвестен.
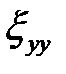 определим из условия несжимаемости:
определим из условия несжимаемости: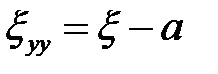 .
.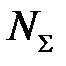 : на
: на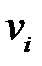 ,
, 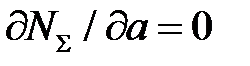 .
.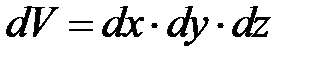 ,
, 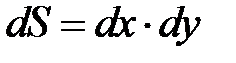 (см. рис. 6.9).
(см. рис. 6.9).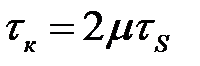 . Рассчитаем интенсивность скоростей деформаций сдвига H при условии, что
. Рассчитаем интенсивность скоростей деформаций сдвига H при условии, что 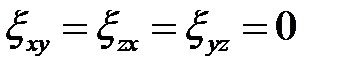 , а скорости линейных деформаций
, а скорости линейных деформаций 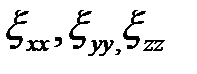 определены выше через параметры а и
определены выше через параметры а и 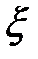 :
: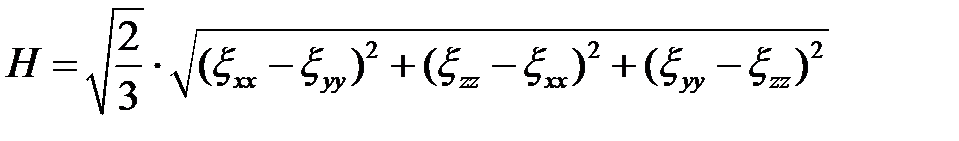 ;
;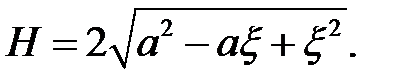 (6.36)
(6.36)
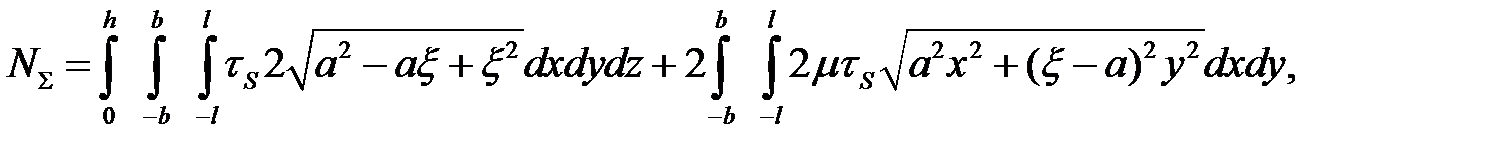
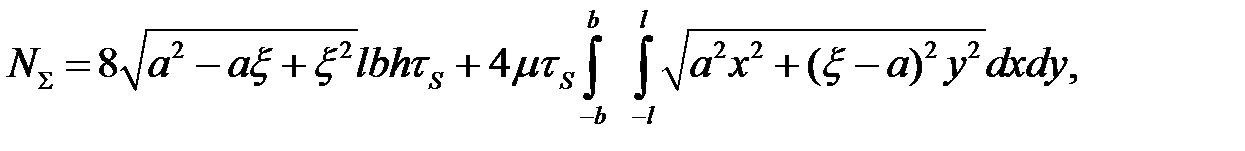 (6.37)
(6.37)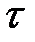 . В начальный момент времени
. В начальный момент времени 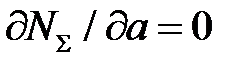 используем формулу (6.37). Получаем
используем формулу (6.37). Получаем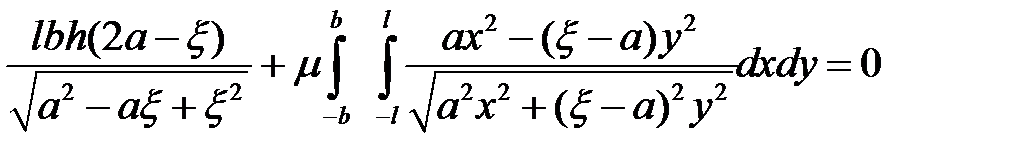 . (6.38)
. (6.38)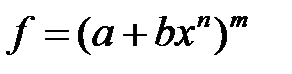 :
: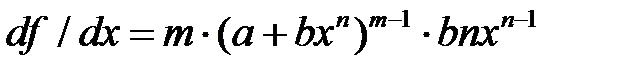 .
.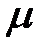 , параметр
, параметр 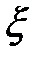 и вычислен двойной интеграл. Интеграл будем вычислять методом ячеек (см. разделы 6.5 и 6.6).
и вычислен двойной интеграл. Интеграл будем вычислять методом ячеек (см. разделы 6.5 и 6.6). . Известно, что средняя скорость деформации
. Известно, что средняя скорость деформации 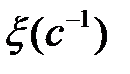 при ковке и горячей объемной штамповке изменяется в следующих пределах: гидравлические прессы – 0.03....0.06; кривошипные прессы – 1...10; молоты – 10...250 [1].
при ковке и горячей объемной штамповке изменяется в следующих пределах: гидравлические прессы – 0.03....0.06; кривошипные прессы – 1...10; молоты – 10...250 [1].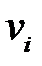 ) и деформации (
) и деформации (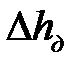 необходимо выполнять шаговым методом. Для этого полное обжатие
необходимо выполнять шаговым методом. Для этого полное обжатие 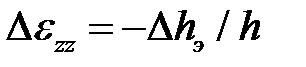 была достаточно мала:
была достаточно мала: 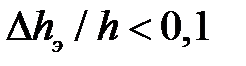 . Здесь
. Здесь 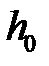 и
и 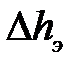 - обжатие на i – ом этапе;
- обжатие на i – ом этапе; 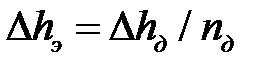 = const;
= const; 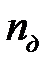 - количество этапов;
- количество этапов; 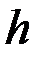 - высота заготовки на этапе;
- высота заготовки на этапе;  .
.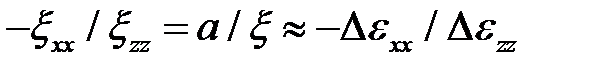 , где
, где 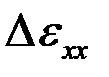 и
и 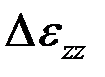 – приращения деформаций. Зная исходные размеры
– приращения деформаций. Зная исходные размеры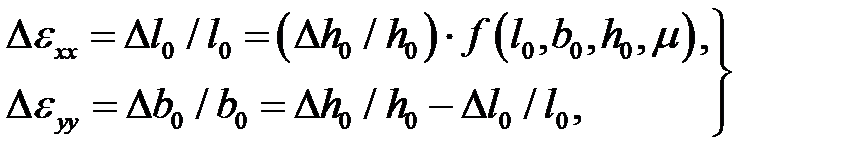 (6.39)
(6.39) при l=l0, b=b0, h=h0,
при l=l0, b=b0, h=h0, 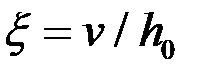 . Затем подсчитывают абсолютную деформацию
. Затем подсчитывают абсолютную деформацию 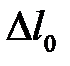 и
и 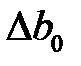 , а также размеры параллелепипеда к началу следующего шага
, а также размеры параллелепипеда к началу следующего шага ,
, 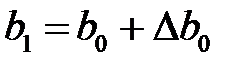 ,
, 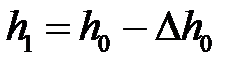 (
(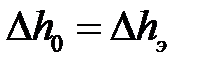 ). (6.40)
). (6.40)
 На этом шаге
На этом шаге 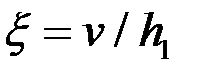 . Затем следует третий шаг и т. д. В итоге решаем задачу расчета формоизменения параллелепипеда.
. Затем следует третий шаг и т. д. В итоге решаем задачу расчета формоизменения параллелепипеда.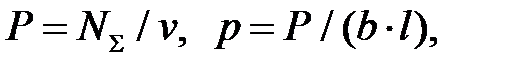 (6.41)
(6.41)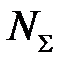 определяется по формуле (6.37).
определяется по формуле (6.37).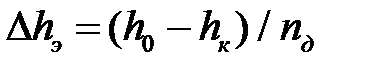 ; принять
; принять 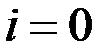 ;
; 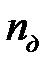 = 10.
= 10.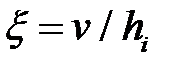 и из уравнения (6.38) определить параметр а.
и из уравнения (6.38) определить параметр а.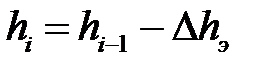 . По известному а и формулам (6.39), (6.40)
. По известному а и формулам (6.39), (6.40)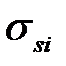 по формуле (6.33) или (6.34) (в зависимости от заданной марки стали); суммарную мощность
по формуле (6.33) или (6.34) (в зависимости от заданной марки стали); суммарную мощность 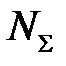 по (6.37); силу Pi и давление pi по формулам (6.41).
по (6.37); силу Pi и давление pi по формулам (6.41).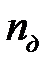 идти к к пункту 3.
идти к к пункту 3. ; (6.5)
; (6.5) . (6.6)
. (6.6)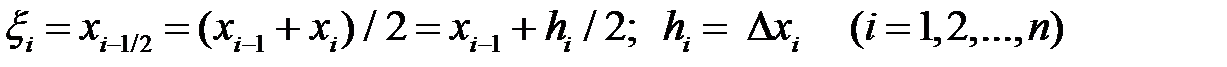 . (6.7)
. (6.7) ; i = 1, 2 ,…, n. (6.8)
; i = 1, 2 ,…, n. (6.8)
 ; (i = 1, 2, …, n). (6.9)
; (i = 1, 2, …, n). (6.9)


