

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Интересное:
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Практические занятия
Занятие №1. Метод Жордана-Гаусса решения систем линейных уравнений
План занятия:
1. Организационный момент.
2. Объяснение нового материала:
1.Система линейных уравнений. Решение системы линейных уравнений. Совместная и несовместная системы уравнений. Определенная и неопределенная системы уравнений. Запись системы уравнений в табличной форме.
2.Эквивалентные системы уравнений. Элементарные преобразования систем линейных уравнений. Теорема об элементарных преобразованиях.
3.Основная переменная. Симплексное преобразование системы линейных уравнений. Полная система основных переменных. Теорема о полной системе основных переменных. Ранг системы уравнений.
4.Алгоритм нахождения полной системы основных переменных.
5.Частное решение системы линейных уравнений. Базисное решение системы линейных уравнений. Опорное решение системы линейных уравнений. Алгоритм нахождения опорного решения.
3.Усвоение и закрепление нового материала.
Решение практических заданий
№1. Решить систему уравнений

Решение
Запишем систему уравнений в виде таблицы и, применяя симплексные преобразования относительно выделенных элементов, получим:
| № | x1 x2 x3 x4 | b |
| 1 1 -3 2 1 -2 0 -1 0 1 1 3 2 -3 2 0 | -6 | |
| 1 -1 -3 2 0 -3 3 -3 0 1 1 3 0 -5 8 -4 | -12 -6 | |
| 1 1 -3 2 0 1 -1 1 0 1 1 3 0 -5 8 -4 | -6 | |
| 1 0 -2 1 0 1 -1 1 0 0 2 2 0 0 3 1 | ||
| 1 0 -2 1 0 1 -1 1 0 0 1 1 0 0 3 1 | ||
| 1 0 0 3 0 1 0 2 0 0 1 1 0 0 0 -2 | -4 | |
| 1 0 0 3 0 1 0 2 0 0 1 1 0 0 0 1 | ||
| 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 |
Отсюда следует, что исходная система уравнений имеет единственное решение
(8, 6, 4, 2).
№2. Решить систему уравнений

Решение
Запишем систему уравнений в виде таблицы и, применяя симплексные преобразования относительно выделенных элементов, получим:
|
|
| № | x1 x2 x3 x4 | b |
| 1 1 -2 1 1 -3 1 1 4 -1 -1 -1 4 3 -4 -1 | ||
| 1 1 -2 1 0 -4 3 0 0 -5 7 -5 0 -1 4 -5 | -1 -3 -2 | |
| 1 1 -2 1 0 -4 3 0 0 -5 7 -5 0 1 -4 5 | -1 -3 | |
| 1 0 2 -4 0 0 -13 20 0 0 -13 20 0 1 -4 5 | -1 | |
| 1 0 2 -4 0 0 -13/20 1 0 1 -4 5 | -1 7/20 | |
| 1 0 -3/5 0 0 0 -13/20 1 0 1 -3/4 0 | 2/5 7/20 1/4 |
Таким образом, система уравнений является неопределенной и (2/5+3/5x3, 1/4+3/4x3, x3, 7/20+13/20 x3) есть общее решение этой системы.
№3. Решить систему уравнений

Решение
Запишем систему уравнений в виде таблицы и, применяя симплексные преобразования относительно выделенных элементов, получим:
| № | x1 x2 x3 x4 | b |
| 6 -5 7 8 3 11 2 4 3 2 3 4 1 1 1 0 | ||
| 0 -11 1 8 0 8 -1 4 0 -1 0 4 1 1 1 0 | ||
| 0 -11 1 8 0 8 -1 4 0 1 0 -4 1 1 1 0 | -1 | |
| 0 0 1 -36 0 0 -1 36 0 1 0 -4 1 0 1 4 | -8 -1 | |
| 0 0 1 -36 0 0 1 -36 0 1 0 -4 1 0 1 4 | -14 -1 | |
| 0 0 0 0 0 0 1 -36 0 1 0 -4 1 0 0 40 | -14 -1 |
Из первой строки последней таблицы следует, что 0=6. Противоречие. Значит, система уравнений решения не имеет.
В задачах №2-№7 найти опорные решения системы линейных уравнений:
№2. 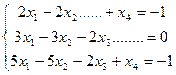 №3.
№3. 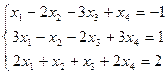
№4.  №5.
№5. 
№6.  №7.
№7. 
4. Подведение итогов занятия.
5. Постановка домашнего задания.
Занятие №2. Понятие задачи линейногопрограммирования
План занятия:
1. Организационный момент.
2. Объяснение нового материала:
1. Понятие экономико-математической модели.
2. Основные этапы решения экономических задач математическими методами.
3. Оптимизационные модели.
4. Модели линейного программирования.
3.Усвоение и закрепление нового материала.
Занятие №7. Теория игр
План занятия:
1. Организационный момент.
2. Объяснение нового материала.
3.Усвоение и закрепление нового материала.
Практические занятия
Занятие №1. Метод Жордана-Гаусса решения систем линейных уравнений
План занятия:
1. Организационный момент.
2. Объяснение нового материала:
1.Система линейных уравнений. Решение системы линейных уравнений. Совместная и несовместная системы уравнений. Определенная и неопределенная системы уравнений. Запись системы уравнений в табличной форме.
|
|
2.Эквивалентные системы уравнений. Элементарные преобразования систем линейных уравнений. Теорема об элементарных преобразованиях.
3.Основная переменная. Симплексное преобразование системы линейных уравнений. Полная система основных переменных. Теорема о полной системе основных переменных. Ранг системы уравнений.
4.Алгоритм нахождения полной системы основных переменных.
5.Частное решение системы линейных уравнений. Базисное решение системы линейных уравнений. Опорное решение системы линейных уравнений. Алгоритм нахождения опорного решения.
3.Усвоение и закрепление нового материала.
|
|
|

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!