Дифференцирование и интегрирование векторных функций

Пусть векторная функция r (t) определена на множестве { t }.

Говорят, что векторная функция r (t) имеет производную в точке t, если существует предел

lim (r (t+Dt)− r (t))/ Dt при Dt ®0

Обозначения: r' (t) ≡ d r (t) / dt.

Геометрический смысл производной векторной функции ясен из рис. 11.

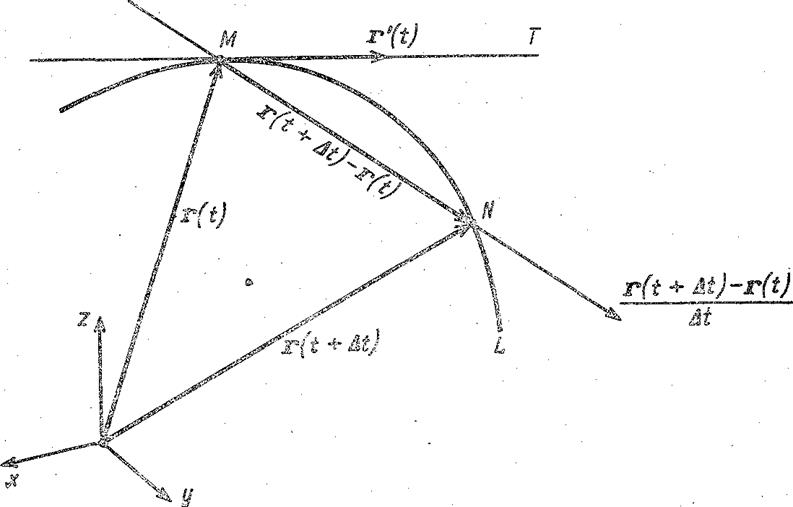
Рис. 11. Вектор r' (t) направлен по касательной к годографу векторной функции r = r (t) в точке М

Если r' (t) ≠ 0, то существует касательная к годографу L векторной функции r (t) в точке М, отвечающей значению t параметра, и вектор r' (t) направлен по этой касательной.

Пусть j(t),y(t),χ(t) — координаты векторной функции r (t).

Если функция r (t) имеет производную в точке t, то каждая из функций j(t),y(t),χ(t) также имеет производную в точке t.

Верно и обратное: если функции j(t),y(t),χ(t) имеют производные в точке t, то и векторная функция r (t) имеет производную в этой точке.

Если каждая из функций r (t), R (t) и λ(t) имеет производную в точке t, то функции r (t)± R (t), λ(t) r (t), r (t)´ R (t), r (t) • R (t) также имеют производные в этой точке, причем выполняются следующие соотношения:

(r ± R) ' = r' ± R', (λ(t) r (t)) ' = λ(t) 'r (t) + λ(t) r (t) ',

Производная векторной функции r' (t) называется второй производной векторной функции r (t). Аналогично определяются третья и последующие производные.

Вторая и третья производные обозначаются соответственно через r "(t) и r '"(t).

Для производных n-го порядка обычно используются обозначения r ^{( n )} (t) или dⁿ r (t) / dtⁿ.

Если j(t),y(t),χ(t) — координаты векторной функции r (t), то

r ⁽ⁿ⁾(t) = j⁽ⁿ⁾(t)i + y⁽ⁿ⁾(t) j + χ⁽ⁿ⁾(t) k. (2)

Если у векторной функции r (t) существуют и непрерывны все производные до порядка n включительно, то пишут r (t) Î Cⁿ.

Пусть функция r (t) Î C^{n- 1} в некоторой окрестности точки t₀ и существует производная r ⁿ(t₀). Тогда для r (t) справедлива формула Тейлора [2]:

Формула (3) получается так.

Разложим координатные функции j(t),y(t),χ(t) вектора r (t) по формуле Тейлора с остаточным членом в форме Пеано[3] o((t-t₀)ⁿ)

Умножая первое соотношение на орт i, второе — на орт j, третье — на орт k, складывая и используя формулы (1) и (2), получим разложение (3).

Интеграл Римана 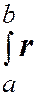(t)dt для векторной функции r (t), a£t£b, определяется как предел интегральных сумм.

Достаточные условия гладкости кривой

ТЕОРЕМА 1 (достаточные условия гладкости в точке).

Пусть кривая L задана векторной функцией r = r (t), имеющей в некоторой окрестности значения t₀Î{t} непрерывную производную r' (t), причем r' (t₀) ≠ 0.

Тогда кривая L является гладкой кривой в точке М₀, отвечающей значению t₀.

 

ТЕОРЕМА 2 (достаточные условия гладкости кривой).

Пусть кривая L задана векторной функцией r = r (t), tÎ{t}, имеющей непрерывную производную r' (t). Если r' (t) ≠ 0 для любого tÎ{t}, то кривая L гладкая.

Поскольку r' (t) ≠ 0, то согласно теореме 1 кривая L является гладкой в любой своей точке. Из условия r' (t) ≠ 0 и непрерывности r' (t) следует непрерывность касательной к кривой L. Значит, L — гладкая кривая.

Регулярные кривые

Пусть гладкая кривая L задана векторной функцией r = r (t). Если r (t) Î Cⁿ, n >2, то кривая L называется регулярной кривой (кривой класса С^п).

Достаточные условия регулярности кривой.

Для того чтобы заданная векторной функцией r (t), tÎ{t}, кривая L была регулярной, достаточно, чтобы на множестве {t} изменения параметра были выполнены следующие условия: r (t) Î Cⁿ, n >2, r' (t) ≠ 0.

Эти условия вытекают из достаточных условий гладкости (теорема 2) и определения регулярности.

Замечание. Если производная r' (t) непрерывна и r' (t₀) ≠ 0, то r' (t) ≠ 0 в некоторой окрестности, значения t₀. Если, кроме того, r (t) Î Cⁿ, n >2, на множестве {t}, то в окрестности точки М₀, отвечающей значению t₀, кривая L регулярная. Тем самым условия r (t) Î Cⁿ, n >2, и r '(t₀) ≠ 0 являются условиями локальной регулярности кривой.

ДЛИНА ДУГИ КРИВОЙ