Простая плоская кривая
Пусть функции j(t) и y(t) аргумента (параметра) t непрерывны на сегменте [ а, b ].
Рассмотрим множество L точек М(х, у), координаты х и у которых определяются соотношениями (рис. 1)
x=j(t), y=y(t), a≤t≤b. (1)
Множество L будем называть простой плоской кривой, если различным значениям параметра t из сегмента [ a, b ] отвечают различные точки этого множества.
Будем говорить также: «соотношения (1) определяют простую плоскую кривую L» и «простая плоская кривая L параметризована при помощи соотношений (1) ».
Если считать параметр t физической величиной — временем, то простую плоскую кривую можно представлять как траекторию движущейся по плоскости точки, причем эта траектория не имеет точек самопересечения и участков самоналегания.
Точки М(х, у), координаты которых определяются соотношениями (1), назовем точками кривой L.
Точки А и В, отвечающие граничным значениям а и b параметра t, назовем граничными точками кривой L.

| Рис. 1. Точка М(х, у) движется по кривой L от точки А до точки В по закону (1)
| Рис. 2. Простая замкнутая кривая L — объединение простых кривых L1 и L2
|
Примером простой плоской кривой может служить график непрерывной на сегменте [ а,b ] функции y=f(x).
Этот график есть множество точек М, координаты х и у которых определяются соотношениями x=t, y=f(t), a≤t≤b.
Ясно, что различным значениям параметра t отвечают различные точки графика.
Замечание 1. Одна и та же простая кривая может быть параметризована различными способами. Можно, например, рассматривать параметризацию простой кривой L, получающуюся из данной ее параметризации x=j(t), y=y(t), a≤t≤b, путем представления параметра t в виде непрерывной строго монотонной функции другого параметра s:
x=j(t(s)), y=y(t(s)), a1≤s≤b1
Замечание 2. Важным является понятие простой замкнутой плоской кривой.
Пусть L1 и L2 — две простые плоские кривые, такие, что:
1) каждая из граничных точек кривой L1, совпадает с одной из граничных точек кривой L2;
2) любые неграничные точки кривых L1 и L2 различны.
Множество L, полученное объединением кривых L1 и L2, называется простой замкнутой плоской кривой.
Простая замкнутая плоская кривая также может быть параметризована при помощи соотношений вида (1) (рис. 2).
Пространственные кривые
Понятие пространственной кривой вводится в полной аналогии с понятием плоской кривой.
Простой пространственной кривой называется множество L точек М пространства, координаты х,у,z которых определяются соотношениями
х=j(t), y=y(t), z=χ(t), a≤t≤b, (5)
где j(t), y(t), χ(t) — функции, непрерывные на сегменте [ а, b ], если различным значениям параметра t из сегмента [ а, b ] отвечают различные точки этого множества.
Используя понятия простой пространственной кривой и разбиения связного множества {t} изменения параметра, приходим так же, как и в случае плоскости, к понятию пространственной кривой, задаваемой параметрическими соотношениями вида (5) при условии монотонного изменения параметра t на, множестве {t}.
Соотношения (5) называют параметрическими уравнениями пространственной кривой.
Замечание. В «n -мерном евклидовом пространстве Еп кривые определяются при помощи соотношений
х1 = j1(t), х2 = j2(t),…,хn = jn(t),
где параметр t изменяется на некотором связном множестве {t}, а функции ji(t) непрерывны.
Касательная к кривой
Пусть кривая L задана параметрическими уравнениями
х=j(t), y=y(t), z=χ(t), tÎ{t}
(функции j(t),y(t),χ(t) непрерывны на множестве {t}).
Обозначим через М0 точку кривой L, отвечающую значению t0 параметра, а через М — точку кривой L, отвечающую значению t параметра из некоторой окрестности значения t0.
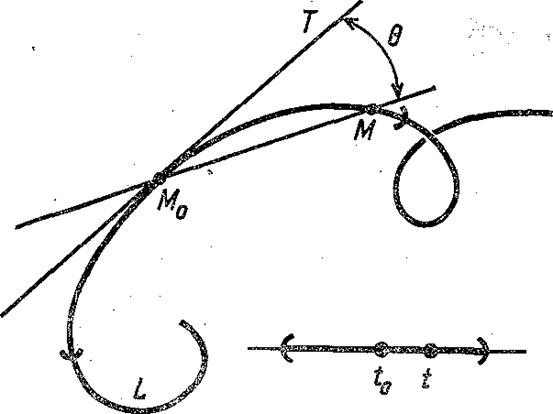
Рис. 9. Окрестность точки М0 на кривой L — множество точек М кривой, отвечающих значениям t параметра из окрестности t0; М0Т — касательная к кривой L в точке М0.
Ясно, что М®М0, если t®t0.
Прямая М0Т называется касательной к кривой L в точке М0, если при М®М0 меньший угол q между этой прямой и переменной прямой М0М стремится к нулю (рис. 9).
Гладкие кривые
Кривая L называется гладкой в точке М0, если в этой точке существует касательная к кривой L и некоторая окрестность точки М0 на кривой L однозначно проектируется на эту касательную.
Точки кривой, в которых она не является гладкой, называются особыми (рис. 10).
Кривая L называется гладкой, если она является гладкой в каждой точке и касательные в точках кривой L изменяются непрерывно. Последнее означает, что если М и N — любые точки кривой L, то при M®N касательная в точке М стремится к касательной в точке N (наименьший угол между этими касательными стремится к нулю).

Рис. 10. а) — кривая L1 не имеет касательной в точке М1;б) — в точке М2 кривая L2 имеет касательную M2T, но никакая окрестность точки М2 на кривой L2 не проектируется однозначно на М2Т (например, точки А и В проектируются в одну и ту же точку С)
Пример. Кривая

гладкая в любой своей точке, но никакая окрестность точки О( 0, 0 ) не является гладкой кривой.
Регулярные кривые
Пусть гладкая кривая L задана векторной функцией r = r (t). Если r (t) Î Cn, n >2, то кривая L называется регулярной кривой (кривой класса Сп).
Достаточные условия регулярности кривой.
Для того чтобы заданная векторной функцией r (t), tÎ{t}, кривая L была регулярной, достаточно, чтобы на множестве {t} изменения параметра были выполнены следующие условия: r (t) Î Cn, n >2, r' (t) ≠ 0.
Эти условия вытекают из достаточных условий гладкости (теорема 2) и определения регулярности.
Замечание. Если производная r' (t) непрерывна и r' (t0) ≠ 0, то r' (t) ≠ 0 в некоторой окрестности, значения t0. Если, кроме того, r (t) Î Cn, n >2, на множестве {t}, то в окрестности точки М0, отвечающей значению t0, кривая L регулярная. Тем самым условия r (t) Î Cn, n >2, и r '(t0) ≠ 0 являются условиями локальной регулярности кривой.
ДЛИНА ДУГИ КРИВОЙ
Свойства длины дуги кривой.
1. Если простая кривая L ' является частью спрямляемой простой кривой L, то кривая L ' также спрямляема.
Всякая ломаная, вписанная в L ', является частью ломаной, вписанной в L (рис. 13). Поэтому множество длин ломаных, вписанных в кривую L ', ограничено, т. е. кривая L ' спрямляема.
Ясно, что длина дуги кривой L ' меньше длины дуги кривой L.
2. Если простая кривая L разбита точкой N на спрямляемые части L ' и L ", то кривая L спрямляема и для длин s(L ' ), s(L " ) и s(L) дуг кривых L ', L " и L выполняется соотношение
s(L ' ) + s(L " ) = s(L).
Рассмотрим произвольную ломаную, вписанную в кривую L (рис. 14).
Добавим к ее вершинам точку N.
Получим новую ломаную, длина которой больше длины исходной ломаной и равна сумме длин ломаных, вписанных в кривые L ' и L ".

| Рис. 14. Объединение ломаных, вписанных в кривые L' и L", правильно вписано в кривую L=L'ÈL"
| Рис. 15. Разбиению отрезка изменения параметра соответствует вписанная в кривую ломаная
|
Отсюда следует, что множество длин ломаных, вписанных в кривую L, ограничено сверху числом s(L ' ) + s(L " ).
Так как мы всегда можем выбрать вписанную в кривую L и содержащую вершину N ломаную так, что ее длина будет отличаться от s(L ' ) + s(L " ) меньше чем на заданную положительную величину, то s(L ' ) + s(L " ) — точная верхняя грань длин ломаных, вписанных в кривую L.
Тем самым s(L) = s(L ' ) + s(L " ).
Пусть А и В — граничные точки спрямляемой кривой L, М — точка кривой L, соответствующая некоторому значению i из сегмента [ а, b ], j(t),y(t),χ(t) — координаты векторной функции r (t).
Обозначим через s(t) длину дуги кривой AM (рис. 15).
3. Функция s(t) строго монотонна и непрерывна на сегменте [ а, b ] и положительна при t > a.
Положительность s(t) очевидна.
Монотонность вытекает из свойства 2.
Доказательство непрерывности предварим вспомогательными рассмотрениями.
а) Пусть e — любое положительное число. Из определения длины дуги вытекает существование вписанной в кривую L ломаной, длина которой отличается от длины кривой L меньше чем на e /2. Естественно рассматривать ломаную, имеющую точку М одной из своих вершин.
Ясно, что и длина части этой ломаной, вписанной в кривую AM, отличается от ее длины s(t) меньше чем на e /2.
Конечно, длина любого звена рассматриваемой ломаной отличается от длины стягиваемой ею дуги меньше чем на e /2.
б) Длины звеньев ломаной со свойством а) можно считать меньше e /2. Действительно, из свойства равномерной непрерывности координат j(t),y(t),χ(t) радиуса-вектора r (t) кривой L на сегменте [ а, b ] вытекает, что по данному e >0 найдется такое положительное число d, что при разбиении сегмента [ а, b ] на частичные сегменты [ ti-1, ti ], t=1, 2, п, с длинами меньше d колебания функций j(t),y(t),χ(t) на каждом частичном сегменте [ ti-1, ti ], будут меньше e /(2Ö3). Тогда длина i-го звена ломаной будет меньше e /2:
в) Рассмотрим ломаную со свойствами а) и б). Дуга, стягиваемая произвольным звеном этой ломаной, имеет длину, меньшую e. В самом деле, по свойству а) длина такой дуги отличается от длины стягивающего ее звена меньше, чем на e /2, а по свойству б) длина любого звена меньше e /2.
Докажем теперь непрерывность функции s(t).
По данному e >0 построим ломаную со свойствами а), б), в) и соответствующее этой ломаной разбиение сегмента [ а, b ]. Пусть точка М на кривой L отвечает значению t=tk.
Обозначим через d наименьшую из длин сегментов [ tk-1,t ], [ t, tk+1 ].
Если 0<Dt<d, то s(t) < s(t+ Dt ) <s(tk+1). Отсюда вытекает, что
0 < s(t+ Dt ) − s(t) < s(tk+1) − s(t) < e,
так как длина дуги, стягиваемой звеном ломаной, меньше e.
Случай (−d)<Dt <0 рассматривается аналогично. Таким образом,
| s(t +Dt ) − s(t) |< e,
если только |Dt|< d.
В силу произвольности выбора точки М на кривой L непрерывность функции s(t) на сегменте [ а, b ] доказана. *
Пусть S — длина кривой L. Вследствие того что функция s=s(t) на сегменте [ а, b ] строго возрастает от нуля до S и непрерывна, на сегменте [0, S]существует строго возрастающая и непрерывная функция t=t(s). Это означает, что параметр t на спрямляемой кривой есть строго монотонная и непрерывная функция длины дуги s. Отсюда следует, что на спрямляемой простой кривой в качестве параметра может быть выбрана длина дуги s.
Такая параметризация спрямляемой кривой называется натуральной или естественной, а параметр s (длина дуги) — натуральным параметром.
Задача. Доказать, что для спрямляемости простой кривой L необходимо и достаточно, чтобы функции j(t),y(t),χ(t) были функциями ограниченной вариации.
Замечание. Понятие длины дуги можно ввести и для кривых, заданных параметрически. Длина дуги такой кривой по определению равна сумме длин простых кривых, из которых она составлена, при условии, что эта сумма ограничена. И в этом случае длина дуги может быть параметром на кривой.
СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ
Кривизна кривой
Определение. Кривизной kx кривой L в точке М0 называется предел отношения Ds при М®М0, где в — наименьший из углов между касательными к кривой L в точках М0 и М, a Ds — длина дуги М0М (рис. 19).
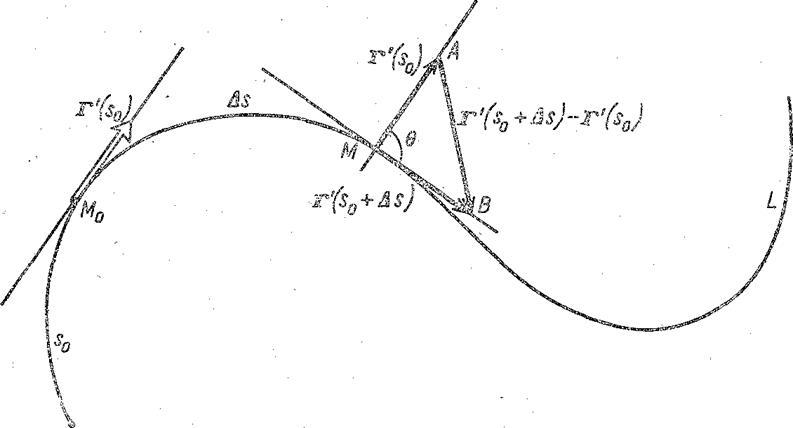
Рис. 19. Длины сторон МА и MB треугольника АВМ равны единице, длина основания АВ равна 2sin(q/2).
Иногда k1 называют первой кривизной кривой.
ТЕОРЕМА 5. Пусть r (t) — вектор кривой L и М0 — точка кривой L, отвечающая значению t0 параметра. Тогда если r' (t0) ≠ 0 и существует r" (t0), то кривая L имеет в точке М0 кривизну k1(t0). Если параметр — длина дуги s, то
k1(s0) =| r "(s0) |.
[1] Вивиани (Viviani) Винченцо (5.4.1622—22.9.1703) — итальянский математик и физик.
[2] Тейлор (Taylor) Брук (18.8.1685—29.12.1731) — английский математик.
[3] Пеано (Реапо) Джузеппе (27.8.1858—20.4.1932) — итальянский математик.
Простая плоская кривая
Пусть функции j(t) и y(t) аргумента (параметра) t непрерывны на сегменте [ а, b ].
Рассмотрим множество L точек М(х, у), координаты х и у которых определяются соотношениями (рис. 1)
x=j(t), y=y(t), a≤t≤b. (1)
Множество L будем называть простой плоской кривой, если различным значениям параметра t из сегмента [ a, b ] отвечают различные точки этого множества.
Будем говорить также: «соотношения (1) определяют простую плоскую кривую L» и «простая плоская кривая L параметризована при помощи соотношений (1) ».
Если считать параметр t физической величиной — временем, то простую плоскую кривую можно представлять как траекторию движущейся по плоскости точки, причем эта траектория не имеет точек самопересечения и участков самоналегания.
Точки М(х, у), координаты которых определяются соотношениями (1), назовем точками кривой L.
Точки А и В, отвечающие граничным значениям а и b параметра t, назовем граничными точками кривой L.

| Рис. 1. Точка М(х, у) движется по кривой L от точки А до точки В по закону (1)
| Рис. 2. Простая замкнутая кривая L — объединение простых кривых L1 и L2
|
Примером простой плоской кривой может служить график непрерывной на сегменте [ а,b ] функции y=f(x).
Этот график есть множество точек М, координаты х и у которых определяются соотношениями x=t, y=f(t), a≤t≤b.
Ясно, что различным значениям параметра t отвечают различные точки графика.
Замечание 1. Одна и та же простая кривая может быть параметризована различными способами. Можно, например, рассматривать параметризацию простой кривой L, получающуюся из данной ее параметризации x=j(t), y=y(t), a≤t≤b, путем представления параметра t в виде непрерывной строго монотонной функции другого параметра s:
x=j(t(s)), y=y(t(s)), a1≤s≤b1
Замечание 2. Важным является понятие простой замкнутой плоской кривой.
Пусть L1 и L2 — две простые плоские кривые, такие, что:
1) каждая из граничных точек кривой L1, совпадает с одной из граничных точек кривой L2;
2) любые неграничные точки кривых L1 и L2 различны.
Множество L, полученное объединением кривых L1 и L2, называется простой замкнутой плоской кривой.
Простая замкнутая плоская кривая также может быть параметризована при помощи соотношений вида (1) (рис. 2).
Плоские кривые, задаваемые параметрически
Истоком такого способа задания кривых служит представление о кривой как о совокупности последовательных положений движущейся точки.
Обратимся к примеру.
Пример 1. Совокупность последовательных положений точки М(х, у), движущейся по плоскости при изменении параметра t от −∞ до +∞ по закону
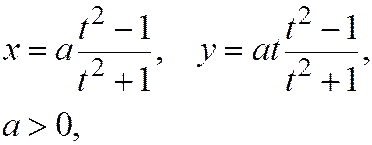
 представляет собой кривую, называемую строфоидой.
представляет собой кривую, называемую строфоидой.
Рис. 3. Строфоида: указан порядок прохождения кривой при изменении параметра t от−∞ до +∞
Заметим, что при изменении параметра t в указанных пределах движущаяся по строфоиде точка М(х, у) попадает в начало координат О (0, 0) дважды: при t= −1 и при t=+1.
Так как мы рассматриваем здесь последовательные положения движущейся точки, то точки строфоиды, отвечающие этим различным значениям параметра t, считаются различными: каждая точка на строфоиде как бы помечается отвечающим этой точке значением параметра t (рис. 3).
Строфоиду можно представить как объединение простых плоских кривых.
В самом деле, разобьем область изменения параметра t, т. е. числовую прямую R, на частичные сегменты [ п, п +1], п =0, ±1, ±2,…
Когда параметр t изменяется на каждом таком сегменте, то соответствующая часть строфоиды — простая кривая.
Ясно, что объединение всех таких частей представляет собой всю строфоиду (рис. 4).
Перейдем теперь к определению кривой, задаваемой параметрически.
Будем считать, что область {t} изменения параметра t — связное множество на прямой:
1) сегмент;
2) полусегмент (полуинтервал) или замкнутая полупрямая;
3) интервал, открытая полупрямая или вся прямая.
Под разбиением D области { t }изменения параметра t на частичные сегменты будем понимать следующую процедуру.

t Î[ -1,0 ] t Î[ 0,1 ] t Î[ 1,2 ]
Рис. 4. Простые участки прямой строфоиды
В случае 1)
– сегмент [ а,b ]разбивается на частичные сегменты [ ti, ti+1 ]при помощи конечного числа точек a=t0 < t1 < t2<... < tn=b.
В случае 2)
– полусегмент [ а, b)или полупрямая [ а, +∞) разбивается на частичные сегменты [ ti, ti+1 ] при помощи точек a=t0 < t1 < t2 < … < tn,
– причем tn® b для полусегмента [ а,b)
– и tn® +∞ для полупрямой [ а, +∞);
– для полусегмента (а, b ]и полупрямой (−∞, b ]разбиение производится при помощи точек
… t-n <...< t-2 < t-1 < t0=b,
– причем t-n®а для полусегмента
– и t-n® −∞ для полупрямой при n®∞.
В случае 3)
– разбиение интервала (а,b), открытой полупрямой (а, + ∞) или всей прямой (− ∞,+ ∞) на частичные сегменты [ tt,ti+1 ]строится при помощи точек
... t-n <...< t-2 < t-1 < t0 < t1 < t2 <…< tn,...,
– причем t-n®а, tn®b для интервала (a, b),
– t-n®a, tn® + ∞ для полупрямой (a, + ∞),
– t-n® − ∞, tn® + ∞ для прямой (− ∞,+ ∞);
– для полупрямой (− ∞, b) t-n® − ∞, tn®b, при n®∞
Пусть функции j(t) и y(t) параметра t непрерывны на связном множестве {t}.
Будем говорить, что соотношения
x = j(t), y=y (t), tÎ{t}, (2)
представляют собой параметрические уравнения плоской кривой L, если существует такое разбиение области {t} на частичные сегменты [ ti, ti+1 ], что при изменении параметра i на каждом таком сегменте соотношения (2) определяют простую плоскую кривую.
Сама кривая L и есть объединение всех указанных простых кривых (с учетом их возможных самопересечений и самоналеганий) при условии монотонного изменения параметра t по множеству {t}.
При этом говорят, что кривая L задана параметрически при помощи соотношений (2).
Пример 2. Соотношения
x=e-tcos t, у=0, 0<t<+∞, (3)
представляют собой параметрически заданную кривую.
Чтобы убедиться в этом, рассмотрим следующее разбиение области { t } = [ 0, + ∞) на частичные сегменты: [ ti, ti+1 ], i=0, 1, 2,..., где ti=p i.
Если t изменяется на таком сегменте, то соотношения (3) определяют простую кривую — сегмент оси Ох с граничными точками
e- p i cos p i и e- p (i+1) cos p(i+1).
Кривая L, определяемая параметрическими уравнениями (3), — это траектория точки, совершающей затухающие колебания на оси Ох с амплитудами 1, е-p, е-2p,... (рис. 5).

Рис. 5. Схематическое изображение кривой, имеющей бесконечное число участков самоналегания
Пример 3. Рассмотрим кривую L, заданную параметрически при помощи соотношений
x=cos(t), y=sin(t), 0≤t≤4 p. (4)
Система сегментов [0,p], [p, 2p], [2p, 3p], [3p, 4p] разбивает множество М=[0, 4p].
Для значений t из каждого сегмента этой системы соотношения (4) определяют простую кривую (полуокружность).
Ясно, что L — окружность, дважды обходимая против часовой стрелки.
Пространственные кривые
Понятие пространственной кривой вводится в полной аналогии с понятием плоской кривой.
Простой пространственной кривой называется множество L точек М пространства, координаты х,у,z которых определяются соотношениями
х=j(t), y=y(t), z=χ(t), a≤t≤b, (5)
где j(t), y(t), χ(t) — функции, непрерывные на сегменте [ а, b ], если различным значениям параметра t из сегмента [ а, b ] отвечают различные точки этого множества.
Используя понятия простой пространственной кривой и разбиения связного множества {t} изменения параметра, приходим так же, как и в случае плоскости, к понятию пространственной кривой, задаваемой параметрическими соотношениями вида (5) при условии монотонного изменения параметра t на, множестве {t}.
Соотношения (5) называют параметрическими уравнениями пространственной кривой.
Замечание. В «n -мерном евклидовом пространстве Еп кривые определяются при помощи соотношений
х1 = j1(t), х2 = j2(t),…,хn = jn(t),
где параметр t изменяется на некотором связном множестве {t}, а функции ji(t) непрерывны.











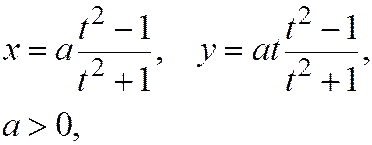
 представляет собой кривую, называемую строфоидой.
представляет собой кривую, называемую строфоидой.




