Классическая механика и границы ее применимости. Материальная точка. Система отсчета. Кинематические уравнения

Классическая механика и границы ее применимости. Материальная точка. Система отсчета. Кинематические уравнения

Классическую механику подразделяют на кинематику, статику и динамику.

Материальная точка- тело, размерами которого можно пренебречь. Движение материальной точки по отношению к системе отсчета может быть задано векторным или координатным способами.

При векторном способе положение точки А, рис. 1, в момент времени t определяется ее радиусом вектором , проведенным из начала координат до движущейся точки.

Закон движения дается векторным уравнением . При координатном способе положение точки А определяется координатами x, y, z, а закон движения задается тремя уравнениями:

при этом

Системой отсчета называется система координат, снабженная часами и жестко связанная с абсолютно твердым телом.

Траектория, путь, перемещение. Средняя и мгновенная скорости. Равномерное прямолинейное движение

Непрерывная линия, которую описывает точка при своем движении, называется траекторией. Путь – это длина траектории, пройденная точкой.

Перемещение- изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения

Мгновенная скорость

Средняя скорость Vср=S/t

Ускорение. Нормальная и тангенциальная составляющие ускорения. Равнопеременное движение

Ускорение- быстрота изменения скорости

Тангенциальное ускорение — компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости

Нормальное ускорение возникает всегда при движении точки по траектории с ненулевой кривизной. Характеризует изменение скорости по направлению.

=

Равнопеременное движение — движение с постоянным ускорением.

V(t)=V0+at

x(t)=x0+V0t+at /2

4 Движение материальной точки по окружности. Угол поворота, угловая скорость, угловое ускорение

Рассмотрим движение материальной точки по окружности радиуса R Пусть за время точка повернется на угол , тогда угловая скорость

,

Угловое ускорение характеризует быстроту изменения угловой скорости, т.е.

 

Сила. Масса. Импульс материальной точки. Второй закон ньютона как уравнение движения

Силой называется векторная величина, характеризующая воздействие на данное тело со стороны других тел.

Импульс материальной точки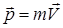

В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

Силы упругости. Закон Гука

закон Гука

Сила упругости F=мюN

F=k x

Вопрос 12

Система материальных точек (МТ) – система, в которой все тела, которые мы рассматриваем, являются МТ.

Внутренние силы – силы взаимодействия между телами системы.

Внешние силы – силы взаимодействия тел из системы с внешними телами.

Замкнутая система – система, в которой отсутствуют внешние силы.

Математический маятник

Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся наневесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения^[1]. Период малых собственных колебанийматематического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен

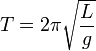
и не зависит^[2] от амплитуды колебаний и массы маятника.

Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.

Уравнение колебаний маятника

Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида

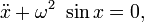
где 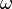― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция 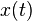― это угол отклонения маятника в момент 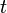от нижнего положения равновесия, выраженный в радианах; 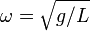, где 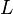― длина подвеса, 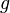― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид:

.

Автоколебания.

Затухающие колебания — колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются.

Закон затухания колебаний определяется свойствами колебательных систем. Обычно рассматривают линейные системы — идеализированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяется. Различные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями.

Дифференциальное уравнение свободных затухающих колебаний линейной системы

 

где s — колеблющаяся величина, описывающая тот или иной физический процесс, δ = const — коэффициент затухания, (ω0 — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при δ =0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы. Решение уравнения рассмотрим в виде

(7.1) где u=u(t).

 

После нахождения первой и второй производных и их подстановки в (1) получим

 

Решение уравнения зависит от знака коэффициента перед искомой величиной. Пусть этот коэффициент положителен:

(7.2)

Тогда получим уравнение решением которого является функция u=A0cos(ωt+φ). Значит, решение уравнения (7.1) в случае малых затуханий

Вопрос 54.

Классическая механика и границы ее применимости. Материальная точка. Система отсчета. Кинематические уравнения

Классическую механику подразделяют на кинематику, статику и динамику.

Материальная точка- тело, размерами которого можно пренебречь. Движение материальной точки по отношению к системе отсчета может быть задано векторным или координатным способами.

При векторном способе положение точки А, рис. 1, в момент времени t определяется ее радиусом вектором , проведенным из начала координат до движущейся точки.

Закон движения дается векторным уравнением . При координатном способе положение точки А определяется координатами x, y, z, а закон движения задается тремя уравнениями:

при этом

Системой отсчета называется система координат, снабженная часами и жестко связанная с абсолютно твердым телом.