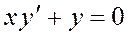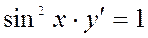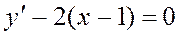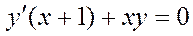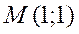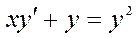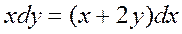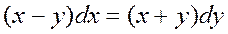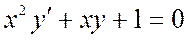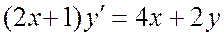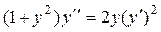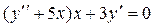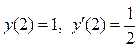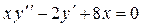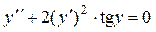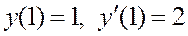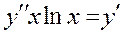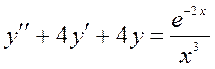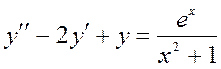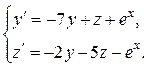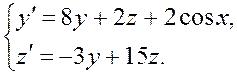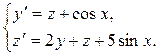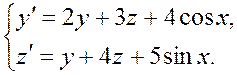Порядка методом повышения порядка
Нормальная система двух линейных дифференциальных уравнений 1-го порядка имеет вид:
 (30)
(30)
где х – независимая переменная, y (x) и z (x) – неизвестные функции, f 1(x) и f 2(x) – известные функции a 1, a 2, b 1, b 2 – коэффициенты. Общее решение системы (30) имеет вид:
 ,
,
где С 1 и С 2 – произвольные постоянные.
Для решения системы (30) методом повышения порядка необходимо исключить одну из неизвестных функций. Для этого можно выразить одну из функций, например, z (x), из одного уравнения системы:
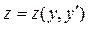 , (31)
, (31)
продифференцировать ее и подставить z и  во второе уравнение системы. После упрощения получаем дифференциальное уравнение 2-го порядка вида
во второе уравнение системы. После упрощения получаем дифференциальное уравнение 2-го порядка вида 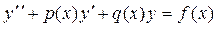 . После получения его решения
. После получения его решения  , следует, используя (31), найти вторую неизвестную функцию:
, следует, используя (31), найти вторую неизвестную функцию:  и записать ответ.
и записать ответ.
Если в системе (30) коэффициенты a 1, a 2, b 1, b 2 – постоянные, то в результате применения метода повышения порядка получается линейное неоднородное уравнение с постоянными коэффициентами:
 ,
,
решение которого рассмотрено в п.5.
Пример использования метода повышения порядка для решения системы двух линейных дифференциальных уравнений 1-го порядка приведен в образце выполнения контрольной работы.
Примерный вариант и образец выполнения
Контрольной работы №6
Задача 1. Дано дифференциальное уравнение 1-го порядка:  и точка
и точка  . Определить тип дифференциального уравнения. Найти общее решение дифференциального уравнения, уравнение интегральной кривой, проходящей через точку М и уравнения еще 4-х интегральных кривых. Построить все эти кривые в системе координат.
. Определить тип дифференциального уравнения. Найти общее решение дифференциального уравнения, уравнение интегральной кривой, проходящей через точку М и уравнения еще 4-х интегральных кривых. Построить все эти кривые в системе координат.
Задача 2. Дано дифференциальное уравнение 1-го порядка:  Определить тип дифференциального уравнения и найти его общее решение.
Определить тип дифференциального уравнения и найти его общее решение.
Задача 3. Дано дифференциальное уравнение 2-го порядка:  и начальные условия:
и начальные условия:  Определить тип дифференциального уравнения и найти его частное решение, удовлетворяющее заданным начальным условиям.
Определить тип дифференциального уравнения и найти его частное решение, удовлетворяющее заданным начальным условиям.
Задача 4. Дано дифференциальное уравнение 2-го порядка:  . Определить тип дифференциального уравнения и найти его общее решение, используя метод вариации произвольных постоянных.
. Определить тип дифференциального уравнения и найти его общее решение, используя метод вариации произвольных постоянных.
Задача 5. Дано дифференциальное уравнение 2-го порядка:  . Определить тип дифференциального уравнения и найти его общее решение, используя метод неопределенных коэффициентов.
. Определить тип дифференциального уравнения и найти его общее решение, используя метод неопределенных коэффициентов.
Задача 6. Дана система линейных дифференциальных уравнений 1-го порядка:  Найти общее решение системы методом повышения порядка.
Найти общее решение системы методом повышения порядка.
Решение задачи 1. Данное дифференциальное уравнение  – уравнение с разделяющимися переменными. Заменим
– уравнение с разделяющимися переменными. Заменим  на
на  и разделим переменные, умножая обе части уравнения на
и разделим переменные, умножая обе части уравнения на 
 .
.
Интегрируя полученное равенство, получим:

откуда  . Заменяя
. Заменяя  , запишем общее решение данного уравнения:
, запишем общее решение данного уравнения:  .
.
Найдем уравнение интегральной кривой, проходящей через точку  , т.е. частное решение, удовлетворяющее заданному начальному условию:
, т.е. частное решение, удовлетворяющее заданному начальному условию:  Для этого подставим в общее решение вместо x, y числа
Для этого подставим в общее решение вместо x, y числа  соответственно:
соответственно:  . Подставляя найденное значение С в общее решение, получим искомое частное решение (уравнение интегральной кривой, проходящей через точку М):
. Подставляя найденное значение С в общее решение, получим искомое частное решение (уравнение интегральной кривой, проходящей через точку М):  .
.
Найдем уравнения еще нескольких интегральных кривых.

 Построим все эти кривые в системе координат (рис.1).
Построим все эти кривые в системе координат (рис.1).
Ответы:  ;
;  ,
,

Интегральные кривые изображены на рис.1.
Решение задачи 2. Данное дифференциальное уравнение  – это уравнение Бернулли, где
– это уравнение Бернулли, где  . Применим подстановку
. Применим подстановку 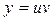 , тогда
, тогда  Подставив значения y и
Подставив значения y и  в уравнение, получим
в уравнение, получим  , или
, или
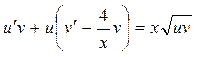 (***)
(***)
Найдем функцию  решая уравнение
решая уравнение 
 .
.
Проинтегрируем левую и правую части этого уравнения:
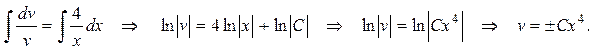
при соответствующем подборе  получаем
получаем  – частное решение уравнения
– частное решение уравнения  .
.
Подставляя найденную функцию  в (***), получим дифференциальное уравнение для функции u:
в (***), получим дифференциальное уравнение для функции u:  или
или  .
.
Найдем функцию  – общее решение этого уравнения:
– общее решение этого уравнения:
 , откуда
, откуда 
Общим решением исходного уравнения является функция
 .
.
Ответ:  .
.
Решение задачи 3. Данное дифференциальное уравнение  – это дифференциальные уравнения 2-го порядка, не содержащие независимой переменной x. Полагаем
– это дифференциальные уравнения 2-го порядка, не содержащие независимой переменной x. Полагаем  = p (y), тогда
= p (y), тогда  и уравнение примет вид:
и уравнение примет вид:

Решая первое уравнение, получим:  – первое семейство решений. Оно не удовлетворяет начальному условию
– первое семейство решений. Оно не удовлетворяет начальному условию 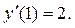
Второе уравнение  есть уравнение с разделяющимися переменными. Разделим переменные, заменяя
есть уравнение с разделяющимися переменными. Разделим переменные, заменяя  на
на  и проинтегрируем:
и проинтегрируем:


где 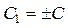 . Производя обратную замену p =
. Производя обратную замену p = 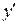 , получим дифференциальное уравнение 1-го порядка относительно неизвестной функции y:
, получим дифференциальное уравнение 1-го порядка относительно неизвестной функции y:
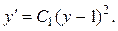
Это уравнение с разделяющимися переменными. Прежде чем его интегрировать, целесообразно определить значение постоянной С 1, используя начальные условия (y = 3, 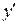 = 2 при х = 1):
= 2 при х = 1):

Подставив значение  в дифференциальное уравнение, получим:
в дифференциальное уравнение, получим:

Разделяя переменные и интегрируя, найдем

Здесь использовано:  .
.
Определим значение постоянной С 2, соответствующее начальному условию y (1) = 3: 
Отсюда искомое частное решение, удовлетворяющее заданным начальным условиям (решение задачи Коши): 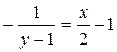 .
.
Получим частное решение уравнения, выразив y (x):

Ответ: 
Решение задачи 4. Данное дифференциальное уравнение  – это линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Его общее решение имеет вид
– это линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Его общее решение имеет вид  . Найдем его в 2 этапа.
. Найдем его в 2 этапа.
1 этап. Построим общее решение  соответствующего однородного уравнения
соответствующего однородного уравнения  . Составим для него характеристическое уравнение
. Составим для него характеристическое уравнение  и найдем его корни:
и найдем его корни:  По таблице 1 определим вид его общего решения
По таблице 1 определим вид его общего решения 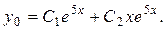
2 этап. Построим частное решение  данного неоднородного уравнения при помощи метода вариации произвольных постоянных. Здесь
данного неоднородного уравнения при помощи метода вариации произвольных постоянных. Здесь  , т.е.
, т.е.  , тогда частное решение
, тогда частное решение  будем искать в виде
будем искать в виде  .
.
Составим условиям вариации согласно (24):
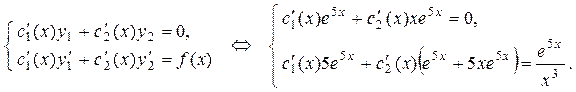
Поделив оба уравнения почленно на  , получим систему с неизвестными
, получим систему с неизвестными 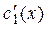 и
и  :
:

Для решения этой системы можно использовать метод исключения. Выразим  из первого уравнения и подставим во второе:
из первого уравнения и подставим во второе:

затем найдем 
Переходим к интегрированию:

(константы интегрирования считаем равными нулю).
Тогда  , и общее решение
, и общее решение  .
.
Ответ: 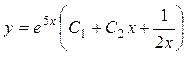 .
.
Решение задачи 5. Данное дифференциальное уравнение  – это линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Его общее решение имеет вид
– это линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Его общее решение имеет вид  . Найдем его в 2 этапа.
. Найдем его в 2 этапа.
1 этап. Построим общее решение  соответствующего однородного уравнения
соответствующего однородного уравнения  Составим для него характеристическое уравнение
Составим для него характеристическое уравнение  и найдем его корни:
и найдем его корни:  По таблице 1 определим вид его общего решения
По таблице 1 определим вид его общего решения 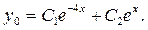
2 этап. Построим частное решение  данного неоднородного уравнения при помощи метода неопределенных коэффициентов. В заданном уравнении
данного неоднородного уравнения при помощи метода неопределенных коэффициентов. В заданном уравнении  – правая часть 2-го специального вида:
– правая часть 2-го специального вида:  , где
, где 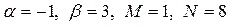 . Числа
. Числа  , тогда, согласно (29), частное решение
, тогда, согласно (29), частное решение  будем искать в виде:
будем искать в виде:

где А и В – неизвестные постоянные. Подставим  в данное неоднородное уравнение:
в данное неоднородное уравнение:

Сократим обе части тождества на  и приравняем коэффициенты при cos3 x и при sin3 x в левой и правой частях тождества.
и приравняем коэффициенты при cos3 x и при sin3 x в левой и правой частях тождества.

Решая полученную систему двух уравнений с двумя неизвестными, находим  Подставив найденные значения А и В в выражение
Подставив найденные значения А и В в выражение  , получим частное решение неоднородного уравнения:
, получим частное решение неоднородного уравнения:

Объединяя результаты 2-х этапов, запишем ответ – общее решение данного уравнения.
Ответ: 
Решение задачи 6. Для решения системы 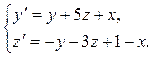 методом повышения порядка исключим из нее одну из функций – z (x).
методом повышения порядка исключим из нее одну из функций – z (x).
Выразим z (x) из первого уравнения системы:  , продифференцируем ее:
, продифференцируем ее:  и подставим z и
и подставим z и  во второе уравнение системы:
во второе уравнение системы:
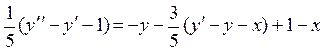 .
.
После упрощения получаем дифференциальное уравнение 2-го порядка:
 .
.
Общее решение этого уравнения имеет вид  . Найдем его в 2 этапа.
. Найдем его в 2 этапа.
1 этап. Построим общее решение  соответствующего однородного уравнения
соответствующего однородного уравнения  . Составим для него характеристическое уравнение
. Составим для него характеристическое уравнение  и найдем корни:
и найдем корни:  – корни комплексные сопряженные. Здесь
– корни комплексные сопряженные. Здесь 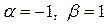 , тогда по таблице 1 определим вид общего решения однородного уравнения:
, тогда по таблице 1 определим вид общего решения однородного уравнения:
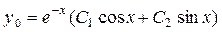 .
.
2 этап. Построим частное решение  неоднородного уравнения. Здесь
неоднородного уравнения. Здесь  – правая часть 1-го специального вида:
– правая часть 1-го специального вида:  , где
, где  , n = 1. Число
, n = 1. Число  не совпадает с корнями характеристического уравнения
не совпадает с корнями характеристического уравнения  , тогда, согласно (28), частное решение
, тогда, согласно (28), частное решение  будем искать в виде:
будем искать в виде:
 ,
,
где А, B – неизвестные коэффициенты, подлежащие определению.
Найдем производные  и подставим
и подставим  в неоднородное уравнение
в неоднородное уравнение  , при этом для простоты используем следующую форму записи:
, при этом для простоты используем следующую форму записи:

(здесь слева от черты записаны коэффициенты, с которыми  входят в уравнение). Приравниваем левую и правую части уравнения после подстановки в него
входят в уравнение). Приравниваем левую и правую части уравнения после подстановки в него  :
:
 .
.
Приравнивая коэффициенты при х 1 и при х 0 в обеих частях тождества, получаем:

откуда находим: A = –1, B = 4. Подставляя найденные значения в  , получим:
, получим:  .
.
Объединяя результаты 2-х этапов, получаем общее решение уравнения  :
:  .
.
Найдем вторую неизвестную функцию:
 Ответ:
Ответ:
 Варианты РГЗ №4
Варианты РГЗ №4
Каждый вариант контрольной работы №6 содержит 6 задач, охватывающих материал по теме «Дифференциальные уравнения».
Перед выполнением контрольной работы необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии с методическими указаниями к выполнению контрольной работы №6, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы.
Интегрирование всех уравнений следует приводить подробно, указывая метод интегрирования.
Вариант контрольной работы соответствует последней цифре студенческого билета
Задача 1. Дано дифференциальное уравнение 1-го порядка и точка М. Определить тип дифференциального уравнения. Найти общее решение дифференциального уравнения, уравнение интегральной кривой, проходящей через точку М и уравнения еще 4-х интегральных кривых. Построить все эти кривые в системе координат.
| № варианта
| Дифференциальное уравнение
| Точка
|
| 1
| 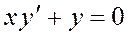
| M (–2; 4)
|
| 2
| 
| M (0; 3)
|
| 3
| 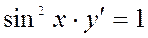
| M 
|
| 4
| 
| M (0; 1)
|
| 5
| 
| M (1; 2)
|
| 6
| 
| M 
|
| 7
| 
| M (0; –1)
|
| 8
| 
| M (0; 1)
|
| 9
| 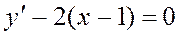
| M (2; 1)
|
| 10
| 
| M (–1; 2)
|
| 11
| 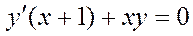
| 
|
| 12
| 
| 
|
| 13
| 
| 
|
| 14
| 
| 
|
| 15
| 
| 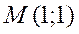
|
| 16
| 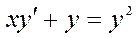
| 
|
| 17
| 
| 
|
| 18
| 
| 
|
| 19
| 
| 
|
| 20
| 
| 
|
Задача 2. Дано дифференциальное уравнение 1-го порядка. Определить тип дифференциального уравнения и найти его общее решение.
| № варианта
| Дифференциальное уравнение
| № варианта
| Дифференциальное уравнение
|
| 1
| 
| 6
| 
|
| 2
| 
| 7
| 
|
| 3
| 
| 8
| 
|
| 4
| 
| 9
| 
|
| 5
| 
| 10
| 
|
| 11
| 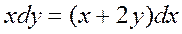
| 12
| 
|
| 13
| 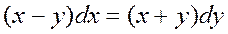
| 14
| 
|
| 15
| 
| 16
| 
|
| 17
| 
| 18
| 
|
| 19
| 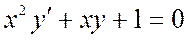
| 20
| 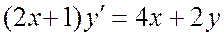
|
Задача 3. Дано дифференциальное уравнение 2-го порядка и начальные условия. Определить тип дифференциального уравнения и найти его частное решение, удовлетворяющее заданным начальным условиям.
| № варианта
| Дифференциальное уравнение
| Начальные условия
|
| 1
| 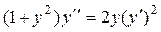
| 
|
| 2
| 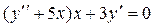
| 
|
| 3
| 
| 
|
| 4
| 
| 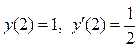
|
| 5
| 
| 
|
| 6
| 
| 
|
| 7
| 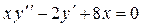
| 
|
| 8
| 
| 
|
| 9
| 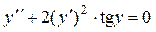
| 
|
| 10
| 
| 
|
| 11
| 
| 
|
| 12
| 
| 
|
| 13
| 
| 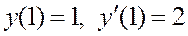
|
| 14
| 
| 
|
| 15
| 
| 
|
| 16
| 
| 
|
| 17
| 
| 
|
| 18
| 
| 
|
| 19
| 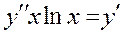
| 
|
| 20
| 
| 
|
Задача 4. Дано дифференциальное уравнение 2-го порядка. Определить тип дифференциального уравнения и найти его общее решение, используя метод вариации произвольных постоянных.
| № варианта
| Дифференциальное уравнение
| № варианта
| Дифференциальное уравнение
|
| 1
| 
| 6
| 
|
| 2
| 
| 7
| 
|
| 3
| 
| 8
| 
|
| 4
| 
| 9
| 
|
| 5
| 
| 10
| 
|
| 11
| 
| 12
| 
|
| 13
| 
| 14
| 
|
| 15
| 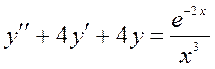
| 16
| 
|
| 17
| 
| 18
| 
|
| 19
| 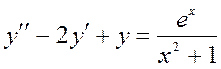
| 20
| 
|
Задача 5. Дано дифференциальное уравнение 2-го порядка. Определить тип дифференциального уравнения и найти его общее решение, используя метод неопределенных коэффициентов.
| № варианта
| Дифференциальное уравнение
| № варианта
| Дифференциальное уравнение
|
| 1
| 
| 6
| 
|
| 2
| 
| 7
| 
|
| 3
| 
| 8
| 
|
| 4
| 
| 9
| 
|
| 5
| 
| 10
| 
|
| 11
| 
| 12
| 
|
| 13
| 
| 14
| 
|
| 15
| 
| 16
| 
|
| 17
| 
| 18
| 
|
| 19
| 
| 20
| 
|
Задача 6. Дана система линейных дифференциальных уравнений 1-го порядка. Найти общее решение системы методом повышения порядка.
| № варианта
| Система
дифференциальных уравнений
| № варианта
| Система
дифференциальных уравнений
|
| 1
| 
| 6
| 
|
| 2
| 
| 7
| 
|
| 3
| 
| 8
| 
|
| 4
| 
| 9
| 
|
| 5
| 
| 10
| 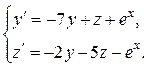
|
| 11
| 
| 12
| 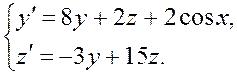
|
| 13
| 
| 14
| 
|
| 15
| 
| 16
| 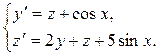
|
| 17
| 
| 18
| 
|
| 19
| 
| 20
| 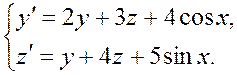
|
Вопросы для самопроверки.
1. Сформулируйте задачу Коши для дифференциальных уравнений 1-го порядка.
2. Методы решения дифференциальных уравнений 1-го порядка: ДУ с разделяющимися переменными, однородные, линейные, уравнения Бернулли. ДУ 2-го порядка, допускающие понижение порядка.
3. Сформулируйте определение обыкновенного дифференциального уравнения 2 порядка.
4. Дайте определение общего и частного решения ДУ 2-го порядка.
5. Сформулируйте задачу Коши ДУ 2-го порядка.
6. Линейные однородные ДУ 2-го порядка. Характеристическое уравнение. Фундаментальная система решений.
7. Дифференциальные уравнения 2 порядка: метод вариации постоянных.
8. Линейные неоднородные дифференциальные уравнения 2 порядка с постоянными коэффициентами. Поиск частного решения уравнений с правой частью специального вида.
Рекомендуемая литература
1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 2 / Д.Т. Письменный. –М.: Рольф, 2002. – 256 с.
2. Щипачев, В.С. Высшая математика: учебник для вузов / В.С. Щипачев.– М.: Высш. шк., 1998.– 479 с.
3. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2 / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова.– М.: Высш. шк., 1999.– 416 с.
4. Щипачев, В.С. Задачник по высшей математике / В.С. Щипачев.– М.: Высш. шк., 2001.– 304 с.



 (30)
(30) ,
,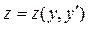 , (31)
, (31) во второе уравнение системы. После упрощения получаем дифференциальное уравнение 2-го порядка вида
во второе уравнение системы. После упрощения получаем дифференциальное уравнение 2-го порядка вида 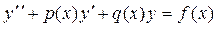 . После получения его решения
. После получения его решения  , следует, используя (31), найти вторую неизвестную функцию:
, следует, используя (31), найти вторую неизвестную функцию:  и записать ответ.
и записать ответ. ,
, и точка
и точка  . Определить тип дифференциального уравнения. Найти общее решение дифференциального уравнения, уравнение интегральной кривой, проходящей через точку М и уравнения еще 4-х интегральных кривых. Построить все эти кривые в системе координат.
. Определить тип дифференциального уравнения. Найти общее решение дифференциального уравнения, уравнение интегральной кривой, проходящей через точку М и уравнения еще 4-х интегральных кривых. Построить все эти кривые в системе координат.  Определить тип дифференциального уравнения и найти его общее решение.
Определить тип дифференциального уравнения и найти его общее решение. и начальные условия:
и начальные условия:  Определить тип дифференциального уравнения и найти его частное решение, удовлетворяющее заданным начальным условиям.
Определить тип дифференциального уравнения и найти его частное решение, удовлетворяющее заданным начальным условиям. . Определить тип дифференциального уравнения и найти его общее решение, используя метод вариации произвольных постоянных.
. Определить тип дифференциального уравнения и найти его общее решение, используя метод вариации произвольных постоянных. . Определить тип дифференциального уравнения и найти его общее решение, используя метод неопределенных коэффициентов.
. Определить тип дифференциального уравнения и найти его общее решение, используя метод неопределенных коэффициентов. Найти общее решение системы методом повышения порядка.
Найти общее решение системы методом повышения порядка. – уравнение с разделяющимися переменными. Заменим
– уравнение с разделяющимися переменными. Заменим  на
на  и разделим переменные, умножая обе части уравнения на
и разделим переменные, умножая обе части уравнения на 
 .
.
 . Заменяя
. Заменяя  , запишем общее решение данного уравнения:
, запишем общее решение данного уравнения:  .
. , т.е. частное решение, удовлетворяющее заданному начальному условию:
, т.е. частное решение, удовлетворяющее заданному начальному условию:  Для этого подставим в общее решение вместо x, y числа
Для этого подставим в общее решение вместо x, y числа  соответственно:
соответственно:  . Подставляя найденное значение С в общее решение, получим искомое частное решение (уравнение интегральной кривой, проходящей через точку М):
. Подставляя найденное значение С в общее решение, получим искомое частное решение (уравнение интегральной кривой, проходящей через точку М):  .
.
 Построим все эти кривые в системе координат (рис.1).
Построим все эти кривые в системе координат (рис.1). ,
,
 – это уравнение Бернулли, где
– это уравнение Бернулли, где  . Применим подстановку
. Применим подстановку 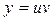 , тогда
, тогда  Подставив значения y и
Подставив значения y и  , или
, или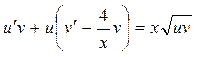 (***)
(***) решая уравнение
решая уравнение 
 .
.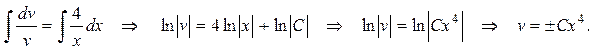
 получаем
получаем  – частное решение уравнения
– частное решение уравнения  .
. в (***), получим дифференциальное уравнение для функции u:
в (***), получим дифференциальное уравнение для функции u:  или
или  .
. – общее решение этого уравнения:
– общее решение этого уравнения: , откуда
, откуда 
 .
. .
. и уравнение примет вид:
и уравнение примет вид:
 – первое семейство решений. Оно не удовлетворяет начальному условию
– первое семейство решений. Оно не удовлетворяет начальному условию 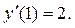
 есть уравнение с разделяющимися переменными. Разделим переменные, заменяя
есть уравнение с разделяющимися переменными. Разделим переменные, заменяя  на
на  и проинтегрируем:
и проинтегрируем: 

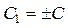 . Производя обратную замену p =
. Производя обратную замену p = 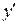 , получим дифференциальное уравнение 1-го порядка относительно неизвестной функции y:
, получим дифференциальное уравнение 1-го порядка относительно неизвестной функции y: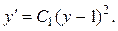

 в дифференциальное уравнение, получим:
в дифференциальное уравнение, получим:

 .
.
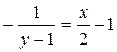 .
.

 – это линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Его общее решение имеет вид
– это линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Его общее решение имеет вид  . Найдем его в 2 этапа.
. Найдем его в 2 этапа. соответствующего однородного уравнения
соответствующего однородного уравнения  . Составим для него характеристическое уравнение
. Составим для него характеристическое уравнение  и найдем его корни:
и найдем его корни:  По таблице 1 определим вид его общего решения
По таблице 1 определим вид его общего решения 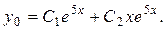
 данного неоднородного уравнения при помощи метода вариации произвольных постоянных. Здесь
данного неоднородного уравнения при помощи метода вариации произвольных постоянных. Здесь  , т.е.
, т.е.  , тогда частное решение
, тогда частное решение  .
.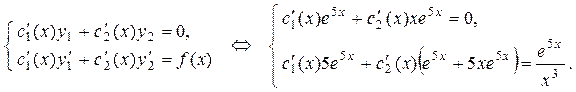
 , получим систему с неизвестными
, получим систему с неизвестными 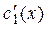 и
и  :
: 
 из первого уравнения и подставим во второе:
из первого уравнения и подставим во второе:


 , и общее решение
, и общее решение  .
.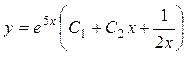 .
. – это линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Его общее решение имеет вид
– это линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Его общее решение имеет вид  . Найдем его в 2 этапа.
. Найдем его в 2 этапа. Составим для него характеристическое уравнение
Составим для него характеристическое уравнение  и найдем его корни:
и найдем его корни:  По таблице 1 определим вид его общего решения
По таблице 1 определим вид его общего решения 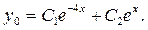
 – правая часть 2-го специального вида:
– правая часть 2-го специального вида:  , где
, где 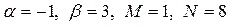 . Числа
. Числа  , тогда, согласно (29), частное решение
, тогда, согласно (29), частное решение  будем искать в виде:
будем искать в виде:
 в данное неоднородное уравнение:
в данное неоднородное уравнение:
 и приравняем коэффициенты при cos3 x и при sin3 x в левой и правой частях тождества.
и приравняем коэффициенты при cos3 x и при sin3 x в левой и правой частях тождества.
 Подставив найденные значения А и В в выражение
Подставив найденные значения А и В в выражение  , получим частное решение неоднородного уравнения:
, получим частное решение неоднородного уравнения:

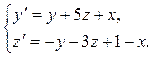 методом повышения порядка исключим из нее одну из функций – z (x).
методом повышения порядка исключим из нее одну из функций – z (x). , продифференцируем ее:
, продифференцируем ее:  и подставим z и
и подставим z и 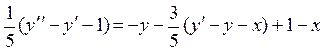 .
. .
. . Найдем его в 2 этапа.
. Найдем его в 2 этапа. соответствующего однородного уравнения
соответствующего однородного уравнения  . Составим для него характеристическое уравнение
. Составим для него характеристическое уравнение  и найдем корни:
и найдем корни:  – корни комплексные сопряженные. Здесь
– корни комплексные сопряженные. Здесь 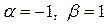 , тогда по таблице 1 определим вид общего решения однородного уравнения:
, тогда по таблице 1 определим вид общего решения однородного уравнения: 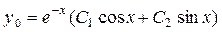 .
. неоднородного уравнения. Здесь
неоднородного уравнения. Здесь  – правая часть 1-го специального вида:
– правая часть 1-го специального вида:  , где
, где  , n = 1. Число
, n = 1. Число  не совпадает с корнями характеристического уравнения
не совпадает с корнями характеристического уравнения  , тогда, согласно (28), частное решение
, тогда, согласно (28), частное решение  ,
, и подставим
и подставим  в неоднородное уравнение
в неоднородное уравнение  , при этом для простоты используем следующую форму записи:
, при этом для простоты используем следующую форму записи: 
 входят в уравнение). Приравниваем левую и правую части уравнения после подстановки в него
входят в уравнение). Приравниваем левую и правую части уравнения после подстановки в него  .
.
 , получим:
, получим:  .
. .
. Ответ:
Ответ: Варианты РГЗ №4
Варианты РГЗ №4