С неотрицательными членами
Признаки сравнения для рядов с неотрицательными членами
Признаки сравнения позволяют свести решение вопроса о сходимости данного ряда к вопросу о сходимости другого более простого ряда или ряда, поведение которого уже выяснено.
Теорема 2.1 (признак сравнения в форме неравенства). Пусть имеются два ряда с неотрицательными членами
 , (2.1)
, (2.1) 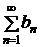 , (2.2)
, (2.2)
причём члены ряда (2.1) не превосходят соответствующих членов ряда (2.2):
0 £ an £ bn,  N. (2.3)
N. (2.3)
Тогда из сходимости ряда (2.2) следует сходимость ряда (2.1), а из расходимости (2.1) ряда следует расходимость ряда (2.2).
►Обозначим через  и
и  частичные суммы этих рядов. Из неравенства (2.3) следует, что
частичные суммы этих рядов. Из неравенства (2.3) следует, что

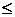
 ,
,  N. (2.4)
N. (2.4)
Пусть ряд (2.2) сходится. Тогда последовательность  ограничена, поэтому в силу (2.4) ограничена и последовательность
ограничена, поэтому в силу (2.4) ограничена и последовательность  . Отсюда заключаем, в силу упомянутой теоремы, что сходится и ряд (2.1).
. Отсюда заключаем, в силу упомянутой теоремы, что сходится и ряд (2.1).
Пусть ряд (2.1) расходится. Надо доказать, что ряд (2.2) также расходится. Предположим противное: этот ряд сходится. Тогда из вышепоказанного следует, что ряд (2.1) сходится. Полученное противоречие с условием расходимости этого ряда доказывает вторую часть теоремы. ◄
Пример 2.1. Доказать, что  сходится.
сходится.
►Имеем:  ,
,  N. Ряд
N. Ряд  сходится, ибо это геометрический ряд
сходится, ибо это геометрический ряд  при
при  (пример 1.1, гл. 1). Тогда в силу теоремы 2.1 сходится и данный ряд.
(пример 1.1, гл. 1). Тогда в силу теоремы 2.1 сходится и данный ряд.
Замечание 2.1. Теорема 2.1 остаётся справедливой, если неравенство (2.1) выполняется не для любого натурального n, а начиная с некоторого m >1 (следствие 1 из теоремы 3.1 гл. 1).
Теорема 2.2 (признак сравнения в предельной форме). Пусть члены рядов
(2.1) и (2.2) строго положительны, т.е. an > 0, bn > 0 для всех n Î N. Если
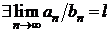 , l ¹ 0, l ¹ +¥,
, l ¹ 0, l ¹ +¥,
то данные ряды сходятся или расходятся одновременно.
Замечание 2.1. Если  , то можно лишь утверждать, что из сходимости ряда
, то можно лишь утверждать, что из сходимости ряда  следует сходимость ряда
следует сходимость ряда  .
.
Замечание 2.2. Для применения признаков сравнения надо иметь арсенал «эталонных рядов», как сходящихся, так и расходящихся, с которыми сравниваются исследуемые ряды. Одним из них является так называемый обобщённый гармонический ряд  . В § 3 будет показано, что он сходится при a > 1 и расходится при a £ 1. Другим «эталонным» рядом является геометрический ряд
. В § 3 будет показано, что он сходится при a > 1 и расходится при a £ 1. Другим «эталонным» рядом является геометрический ряд  , сходящийся при | q | < 1 и расходящийся при | q | ³ 1 (пример 1.1).
, сходящийся при | q | < 1 и расходящийся при | q | ³ 1 (пример 1.1).
Следствие 2.1 из теоремы 2.2. Пусть дан ряд  с положительными членами, причём
с положительными членами, причём  при
при 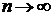 . Если
. Если  при n ® ¥, где С – постоянное число, тогда рассматриваемый ряд сходится при a > 1 и расходится при 0 ≤ a £ 1 (здесь ~ является знаком эквивалентности).
при n ® ¥, где С – постоянное число, тогда рассматриваемый ряд сходится при a > 1 и расходится при 0 ≤ a £ 1 (здесь ~ является знаком эквивалентности).
Пример 2.3. Исследовать на сходимость ряд  .
.
►Имеем:  при n ® ¥. В этом случае a = 2 > 1, следовательно, данный ряд сходится (следствие 2.1).◄
при n ® ¥. В этом случае a = 2 > 1, следовательно, данный ряд сходится (следствие 2.1).◄
Интегральный признак Коши
Теорема 3.1 (интегральный признак Коши). Пусть функция f (x) непрерывна, положительна и убывает при x ³ 1. Тогда ряд  , где an = f (n) для
, где an = f (n) для 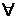 n Î N, и несобственный интеграл
n Î N, и несобственный интеграл 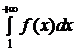 либо оба сходятся, либо оба расходятся.
либо оба сходятся, либо оба расходятся.
Пример 3.1. Исследовать на сходимость обобщённый гармонический ряд  в зависимости от значения параметра a.
в зависимости от значения параметра a.
► Заметим, что при a £ 0 общий член ряда не стремится к нулю с увеличением номера, следовательно, не выполняется необходимое условие сходимости ряда, поэтому в этом случае обобщённый гармонический ряд расходится.
При a = 1 получаем гармонический ряд, он расходится.
В случае a > 0, a ≠ 1 рассмотрим функцию  . Легко проверить, что она удовлетворяет при x ³ 1 всем условиям теоремы 3.1. Исследуем на сходимость несобственный интеграл
. Легко проверить, что она удовлетворяет при x ³ 1 всем условиям теоремы 3.1. Исследуем на сходимость несобственный интеграл  при данных значениях a.
при данных значениях a.
1. 0 < a < 1Þ 1 - a > 0 Þ  – несобственный интеграл расходится и, следовательно, рассматриваемый ряд расходится при 0 < a < 1.
– несобственный интеграл расходится и, следовательно, рассматриваемый ряд расходится при 0 < a < 1.
2. a > 1 Þ 1 - a < 0 Þ 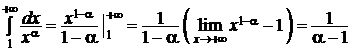 , поэтому несобственный интеграл сходится, а вместе с ним сходится и обобщённый гармонический ряд при указанных значениях a.
, поэтому несобственный интеграл сходится, а вместе с ним сходится и обобщённый гармонический ряд при указанных значениях a.
Итак, ряд  расходится при a £ 1 и сходится при a > 1. ◄
расходится при a £ 1 и сходится при a > 1. ◄
Пример 3.2. Исследовать сходимость ряда  .
.
►Пусть  . Легко проверить, что функция f (x) удовлетворяет всем условиям теоремы 3.1. Но интеграл
. Легко проверить, что функция f (x) удовлетворяет всем условиям теоремы 3.1. Но интеграл


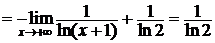 сходится.
сходится.
Следовательно, сходится и данный ряд.◄



 , (2.1)
, (2.1) 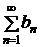 , (2.2)
, (2.2) N. (2.3)
N. (2.3) и
и  частичные суммы этих рядов. Из неравенства (2.3) следует, что
частичные суммы этих рядов. Из неравенства (2.3) следует, что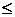
 сходится.
сходится. ,
,  сходится, ибо это геометрический ряд
сходится, ибо это геометрический ряд  при
при  (пример 1.1, гл. 1). Тогда в силу теоремы 2.1 сходится и данный ряд.
(пример 1.1, гл. 1). Тогда в силу теоремы 2.1 сходится и данный ряд.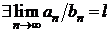 , l ¹ 0, l ¹ +¥,
, l ¹ 0, l ¹ +¥, , то можно лишь утверждать, что из сходимости ряда
, то можно лишь утверждать, что из сходимости ряда  следует сходимость ряда
следует сходимость ряда  .
. . В § 3 будет показано, что он сходится при a > 1 и расходится при a £ 1. Другим «эталонным» рядом является геометрический ряд
. В § 3 будет показано, что он сходится при a > 1 и расходится при a £ 1. Другим «эталонным» рядом является геометрический ряд  , сходящийся при | q | < 1 и расходящийся при | q | ³ 1 (пример 1.1).
, сходящийся при | q | < 1 и расходящийся при | q | ³ 1 (пример 1.1). при
при 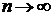 . Если
. Если  при n ® ¥, где С – постоянное число, тогда рассматриваемый ряд сходится при a > 1 и расходится при 0 ≤ a £ 1 (здесь ~ является знаком эквивалентности).
при n ® ¥, где С – постоянное число, тогда рассматриваемый ряд сходится при a > 1 и расходится при 0 ≤ a £ 1 (здесь ~ является знаком эквивалентности). .
. при n ® ¥. В этом случае a = 2 > 1, следовательно, данный ряд сходится (следствие 2.1).◄
при n ® ¥. В этом случае a = 2 > 1, следовательно, данный ряд сходится (следствие 2.1).◄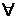 n Î N, и несобственный интеграл
n Î N, и несобственный интеграл 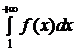 либо оба сходятся, либо оба расходятся.
либо оба сходятся, либо оба расходятся. . Легко проверить, что она удовлетворяет при x ³ 1 всем условиям теоремы 3.1. Исследуем на сходимость несобственный интеграл
. Легко проверить, что она удовлетворяет при x ³ 1 всем условиям теоремы 3.1. Исследуем на сходимость несобственный интеграл  при данных значениях a.
при данных значениях a. – несобственный интеграл расходится и, следовательно, рассматриваемый ряд расходится при 0 < a < 1.
– несобственный интеграл расходится и, следовательно, рассматриваемый ряд расходится при 0 < a < 1.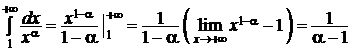 , поэтому несобственный интеграл сходится, а вместе с ним сходится и обобщённый гармонический ряд при указанных значениях a.
, поэтому несобственный интеграл сходится, а вместе с ним сходится и обобщённый гармонический ряд при указанных значениях a. .
. . Легко проверить, что функция f (x) удовлетворяет всем условиям теоремы 3.1. Но интеграл
. Легко проверить, что функция f (x) удовлетворяет всем условиям теоремы 3.1. Но интеграл

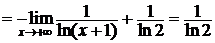 сходится.
сходится.
