
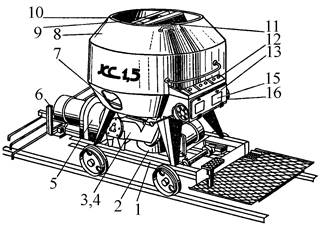
Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Интересное:
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Определение. Ряд называется знакочередующимся, если каждые два соседние его слагаемые имеют разный знак: 
Сформируем достаточный признак сходимости такого ряда.
ТЕОРЕМА 1 (признак Лейбница). Пусть ряд  знакочередующийся, последовательность
знакочередующийся, последовательность  монотонно убывает и
монотонно убывает и 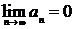 . Тогда ряд (1) сходится, его сумма
. Тогда ряд (1) сходится, его сумма  .
.
Следствие.  , то есть погрешность приближённого вычисления знакочередующегося ряда по частичной сумме не превосходит абсолютной величины первого отброшенного члена.
, то есть погрешность приближённого вычисления знакочередующегося ряда по частичной сумме не превосходит абсолютной величины первого отброшенного члена.
Пример 1. Сколько слагаемых нужно взять, чтобы вычислить  с точностью до 0,001?
с точностью до 0,001?
Решение. Можно записать два неравенства:

Найдём  :
:  . Ответ: 31 слагаемое.
. Ответ: 31 слагаемое.
Ряды с произвольным членами, абсолютная и условная сходимости.
Определение. Ряд называется знакопеременным, если его общий член может быть как положительным, так и отрицательным.
Определение. Ряд 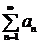 сходится абсолютно, если сходится ряд
сходится абсолютно, если сходится ряд  .
.
Определение. Сходящийся ряд, который не сходится абсолютно, называется условно сходящимся.
ТЕОРЕМА 2. Из сходимости ряда  следует сходимость ряда
следует сходимость ряда 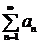 .
.
Абсолютная сходимость  сходимость, сходимость
сходимость, сходимость  абсолютная сходимость.
абсолютная сходимость.
Замечание. Каждый из рассмотренных нами признаков сходимости знакоположительных рядов может рассматриваться как достоверный признак абсолютной сходимости.
Члены абсолютно сходящегося ряда можно менять местами произвольным образом. Для условно сходящегося — это неверно.
ТЕОРЕМА 3 (Дирихле). Пусть ряд  сходится абсолютно и его сумма равна
сходится абсолютно и его сумма равна  . Тогда ряд
. Тогда ряд  , полученный из
, полученный из  произвольной перестановкой его членов также сходится абсолютно, причём к той же сумме
произвольной перестановкой его членов также сходится абсолютно, причём к той же сумме  (без доказательства).
(без доказательства).
ТЕОРЕМА 4 (Римана). Пусть ряд  сходится условно,
сходится условно,  . Тогда члены ряда можно переставить так, что его сумма будет равна
. Тогда члены ряда можно переставить так, что его сумма будет равна  .
.
|
|
Функциональные ряды.
Определение. Пусть  — функции, заданные на
— функции, заданные на  . Тогда ряд.
. Тогда ряд.  называется функциональным рядом.
называется функциональным рядом.
Определение. Ряд называется  сходящимся на множестве
сходящимся на множестве  , если в каждой точке
, если в каждой точке  ряд сходится как числовой.
ряд сходится как числовой.
Определение. Функциональный ряд  равномерно сходится на множестве
равномерно сходится на множестве  , если
, если  и
и  . Здесь
. Здесь  ,
,  .
.
Пример 1. Геометрический ряд 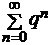 — сходится, если
— сходится, если  , расходится при
, расходится при  . Рассмотрим функциональный ряд:
. Рассмотрим функциональный ряд:  . Этот ряд сходится, если
. Этот ряд сходится, если  (расходится при
(расходится при  ) и его сумма
) и его сумма  при
при  .
.
Определение: Функциональный ряд  мажорируется на множестве
мажорируется на множестве  сходящимся числовым рядом
сходящимся числовым рядом  , если
, если 

ТЕОРЕМА 1 ((Достаточный) признак Вейерштрасса равномерной сходимости функционального ряда). Пусть ряд  (1) мажорируется на
(1) мажорируется на  сходящимся числовым рядом
сходящимся числовым рядом  (2). Тогда ряд равномерно сходится на
(2). Тогда ряд равномерно сходится на  .
.
Примеры 2-3: Функциональные ряды  равномерно сходятся на
равномерно сходятся на  , так как они мажорируются
, так как они мажорируются 
Степенные ряды.
Определение. Функциональный ряд вида  (1) называется степенным. Здесь
(1) называется степенным. Здесь  — коэффициенты,
— коэффициенты,  — центр степенного ряда. Определение: множество
— центр степенного ряда. Определение: множество  точек числовой оси, где сходится ряд (1), называются его областью сходимости.
точек числовой оси, где сходится ряд (1), называются его областью сходимости.
ТЕОРЕМА 1 (Абеля): 1) Если степенной ряд (1) сходится в точке  , то он сходится, причём абсолютно,
, то он сходится, причём абсолютно,  .
.
2) Если ряд расходится в точке  , то он расходится,
, то он расходится,  .
.
Область сходимости степенного ряда всегда - промежуток с центром в точке, причём этот промежуток может являться интервалом или полуинтервалом или отрезком.
Определение: радиусом сходимости степенного ряда (1) называется число 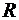 : при
: при  ряд сходится, а вне этого интервала — расходится. Если
ряд сходится, а вне этого интервала — расходится. Если  , то интервал вырождается в точку
, то интервал вырождается в точку  (в своём центре сходится любой степенной ряд!);
(в своём центре сходится любой степенной ряд!);  — интервал сходимости представляет собой всю числовую ось. Сформулируем результаты, позволяющие вычислить радиус сходимости степенного ряда.
— интервал сходимости представляет собой всю числовую ось. Сформулируем результаты, позволяющие вычислить радиус сходимости степенного ряда.
ТЕОРЕМА 2 (Коши-Адамар): Пусть существует  .
.
Тогда ряд сходится при  и расходится вне этого интервала. Если
и расходится вне этого интервала. Если  , то
, то  , если
, если  , то
, то  .
.
|
|
ТЕОРЕМА 3 (Даламбера). Пусть 
Тогда степенной ряд (1) сходится внутри интервала  и расходится вне его.
и расходится вне его.
Замечания:
1) При  , то есть на концах интервала, теоремы 2 и 3 ответа на вопрос о сходимости не дают. В этих точках требуется отдельное исследование.
, то есть на концах интервала, теоремы 2 и 3 ответа на вопрос о сходимости не дают. В этих точках требуется отдельное исследование.
2) В каждой из этих точек, как показывают примеры ниже, ряд может как сходиться, так и расходиться.
Пример 1: степенной ряд:  . Его
. Его 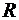 сходимости
сходимости  , при
, при  ряд расходится как гармонический;
ряд расходится как гармонический;  , сходится как ряд Лейбница. Таким образом
, сходится как ряд Лейбница. Таким образом 
Определение: интервалом сходимости принято называть  .
.
ТЕОРЕМА 4: Пусть степенной ряд (1) сходится на интервале  . Тогда
. Тогда 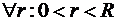 ряд равномерно сходится на отрезке
ряд равномерно сходится на отрезке 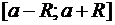 .
.
СВОЙСТВА СТЕПЕННЫХ РЯДОВ.
Следствие 1: Сумма степенного ряда является непрерывной функцией на всём интервале его сходимости.
Замечание: на отрезке 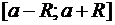 сумма степенного ряда может быть разрывной.
сумма степенного ряда может быть разрывной.
Пример 3: геометрический ряд  сходится на интервале
сходится на интервале  и его сумма
и его сумма  непрерывна на этом интервал, но имеет разрыв на правом конце
непрерывна на этом интервал, но имеет разрыв на правом конце 
Следствие 2: степенной ряд (1) можно почленно дифференцировать в интервале сходимости; при этом ряд, составленный из производных:
1) также является степенным;
2) имеет тот же радиус сходимости;
3) имеет сумму равную производной суммы исходного ряда (в каждой точке интервала сходимости). (без доказательства)
Следствие 3: степенной ряд можно почленно интегрировать на отрезке  с
с  ; полученный ряд имеет вид
; полученный ряд имеет вид  и имеет тот же радиус сходимости.
и имеет тот же радиус сходимости.
1. Формула Тейлора.
Определение. Пусть 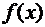 дифференцируема до порядка
дифференцируема до порядка  включительно в некоторой окрестности точки
включительно в некоторой окрестности точки  . Тогда многочлен Тейлора
. Тогда многочлен Тейлора  или
или  определяется по формуле
определяется по формуле  (1)
(1)
изависит от функции 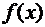 ,
,  , точки
, точки  .
.
Определение. Величину  (2) назовём остаточным членом формулы Тейлора (остатком).
(2) назовём остаточным членом формулы Тейлора (остатком).
Свойства остаточного члена: 1)  . 2)
. 2)  , при
, при  .
.
3) Пусть  в окрестности точки
в окрестности точки  . Тогда
. Тогда  .
.
ТЕОРЕМА 1 (Формула Тейлора с остаточным членом в форме Пеано).
Пусть функция 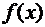 имеет в точке
имеет в точке  все производные до порядка
все производные до порядка  включительно.
включительно.
Тогда в некоторой окрестности точки  имеет место представление:
имеет место представление:
 Доказательство: Вычислим, последовательно применяя правило Лопиталя:
Доказательство: Вычислим, последовательно применяя правило Лопиталя:

 .
.
ТЕОРЕМА 2 (Формула Тейлора с остаточным членом в форме Лагранжа):
Пусть функция 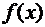 имеет все производные до порядка
имеет все производные до порядка  включительно на конечном отрезке
включительно на конечном отрезке  . Тогда
. Тогда 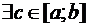 :
:

 . (3)
. (3)
Ряды Тейлора и Маклорена.
|
|
Пусть степенной ряд  (4) имеет радиус сходимости
(4) имеет радиус сходимости 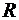 . Тогда на
. Тогда на  ряд (4) сходится к
ряд (4) сходится к 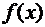 (сумме ряда).
(сумме ряда).  (6)
(6)
Определение: Ряд (4), где коэффициенты определяются по формуле (6) называются рядом Тейлора функции 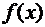 в определённой точке
в определённой точке  .
.
 .
.
Определение: При  ряд Тейлора называется рядом Маклорена.
ряд Тейлора называется рядом Маклорена.
Степенной ряд (4) является рядом Тейлора для своей суммы 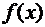 на интервале сходимости.
на интервале сходимости.
Определение: функция 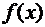 называется разложимой в ряд Тейлора в окрестности точки
называется разложимой в ряд Тейлора в окрестности точки  , если её ряд Тейлора сходится к
, если её ряд Тейлора сходится к 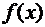
 , где
, где 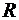 — радиус сходимости ряда Тейлора.
— радиус сходимости ряда Тейлора.
ТЕОРЕМА 3: (Необходимое и достаточное условие). Функция  разложима в ряд Тейлора на множестве
разложима в ряд Тейлора на множестве  если и только если
если и только если 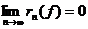 для всех
для всех 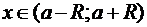 .
.
|
|
|

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!