

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...
Топ:
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Интересное:
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Содержание
Введение…………………………………………………………………. 1. Математические операции криптографических систем ………….
2. Генерация ключей для шифрования на основе конечных полей …
3. Симметричные и асимметричные системы шифрования………..
3.1. Криптографическая система защиты информации на основе стандарта AES (Rijndael)…………………………………….
3.2. Асимметричная система шифрования RSA…………………….
4. Алгоритм формирования хэш – функции ……………………………
5. Криптографическая защита передаваемых данных с помощью
программной системы PGP………………………………………………
5.1.Стандарт OpenPGP……………………………………………….
5.2.Система открытого распределения ключей …………………..
5.3.Электронная цифровая подпись ………………………………
5.4.Цифровая подпись Эль-Гамаля ……………………………….
5.5.Состав системы PGP 8.0 ……………………………………….
5.6. Генерация асимметричных ключей …………………………..
5.7. Порядок генерации ключей в системе PGP…………………..
5.8. Обмен открытыми ключами……………………………………
5.9. Передача открытого ключа файлом……………………………
5.10. Пересылка открытого ключа по электронной почте………..
5.11.Обмен открытыми ключами через сервер ключей………….
5.12.Модель заверения и проверки подлинности открытых
ключей………………………………………………………………………….
5.13. Формирование цифровой подписи……………………………….
5.14. Добавление и изменение владельцев асимметричных ключей………………………………………………………………………….
5.15. Отзыв и удаление ключей, а также наложение запрета на их
использование……………………………………………………………………
5.16. Защита файлов ключей…………………………………………….
5.17. Криптографическая защита файлов и сообщений……………
|
|
5.18. Шифрование или одновременно шифрование и подписывание
файлов……………………………………………………………………………
5.19. Подписывание файлов…………………………………………..
5.20. Расшифровывание файлов и проверка их цифровых подписей…
5.21. Криптографическая защита сообщений электронной почты……
5.22. Отправка и получение защищенного файла вместе с почтовым сообщением………………………………………………………………………
5.23.Гарантированное удаление файлов……………………………….
6. Описание лабораторных работ ………………………………..........
Лабораторная работа №1. Математические операции в криптографических системах……………………………………………………
Лабораторная работа №2. Генерация ключей для шифрования
на основе конечных полей ………………………………………………………
Лабораторная работа №3. Криптографическая система
шифрования информации на основе стандарта AES (Rijndael)…………………
Лабораторная работа №4. Криптографическая система дешифрования информации на основе стандарта AES (Rijndael)………………
Лабораторная работа №5. Асимметричная криптографическая система шифрования RSA………………………………………………………………….
Лабораторная работа №6. Изучение алгоритма хэш – функции системы SHA – 1…………………………………………………………………
Лабораторная работа №7. Генерация открытых и закрытых ключей
шифрования ………………………………………………………………………
Лабораторная работа №8. Криптографическая защита
передаваемых данных с помощью системы PGP………………………………
Список литературы ………………………………………………………
Приложение 1. Список простых чисел до 6000 ………………………….
Приложение 2. Таблица неприводимых многочленов над полем 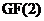 …
…
Приложение 3. Система шифрования по стандарту AES…………………
Приложение 4. Условные обозначения на схемах математических функций…………………………………………………………………………….
Приложение 5. Таблица 1. Таблица замен S – box.
Таблица 2. Таблица замен S -1– box……………………..
Приложение 6. Система дешифрования по стандарту AES………………
|
|
Приложение 7. Генерация элементов поля Галуа GF(2m)………………
Введение
Мировое сообщество вступило в новую эпоху, когда производственная или коммерческая деятельность, финансовые транзакции, обмен военными или правительственными документами все более часто осуществляются через открытые глобальные (ГВС) или локальные (ЛВС) вычислительные сети. Любой человек или организация может воспользоваться и пользуется услугами этих сетей. Однако, часто обрабатываемая, хранимая или передаваемая информация имеет конфиденциальный или секретный характер. Поэтому остро встал вопрос защиты такой информации от активных и пассивных атак злоумышленников. Значительная роль при защите информации отводится криптологии, составными частями которой являются криптография и криптоанализ [2,5,12]. Эти две составные части криптологии решают противоположные задачи и в настоящее время бурно развиваются на основе совершенствования вычислительных средств и математических методов. Криптографические методы защиты берут за основу теорию, которая включает четкие математические методы засекречивания с необходимой степенью секретности на основе симметричных и асимметричных криптографических систем, методы генерации и распространения открытых и закрытых ключей информации, аутентификацию и управление доступом к информации, методы формирования и проверки электронной цифровой подписи. Криптоанализ развивается в направлении совершенствования и создания новых средств взлома секретной информации на основе линейного и дифференциального криптоанализа, методов Полларда, метода разложения больших чисел на простые сомножители, методов дискретного логарифмирования.
Здесь также отметим, большое значение административных мер защиты информации, при которых необходим учет большого количества организационных факторов и правильный выбор правил, структуры и состава средств защиты информации. Обратим также внимание на развитие активных способов воздействия на информацию, которые направлены на модификацию, уничтожение или переадресацию информации, а также на изменение категории и прав пользователей. Сюда следует отнести усовершенствованные программы типа «троянский конь», программы «вирусы», «спамы» и «черви», которые ведут к огромным потерям материальных, трудовых и информационных ресурсов.
|
|
Криптографическая защита и криптографический анализ информации обеспечивают необходимый уровень защиты информации, ее подлинности, и достоверности, а также необходимый уровень управления доступом в ней.
В настоящее время разработано множество стандартных средств защиты информации и управления доступом к ней. Среди них необходимо отметить средства защиты, применяемые в сети Internet, такие протоколы, как: IPSec - протокол обеспечения безопасности в Internet, IKE-протокол обмена ключами через Internet, SSH-протокол удаленной регистрации, Kerberos-5 – протокол аутентификации пользователей и управления их доступом к услугам сети [2,9,10].
Для защиты передаваемой в сетях и хранимой информации широкое распространение получила система PGP 8 (Pretty Good Privacy – очень высокая секретность).
В 2001 году в США принят новый стандарт шифрования симметричным блочным шифром AES (Advanced Encryption Standart) c гарантированной криптографической стойкостью.
Одновременно в России и США в 2001 году опубликованы стандарты электронной цифровой подписи (ЭЦП) на основе эллиптических кривых, которые при длине ключа в 128 бит обеспечивают более высокую криптостойкость, чем аналогичные асимметричные системы с длинной ключа порядка 1024 бит.
В данных методических указаниях изучаются основы криптографической защиты информации: математические основы защиты информации, генерация ключей на основе псевдослучайных последовательностей, асимметричное шифрование на основе алгоритма RSA (Rivest, Shamir, Adlemen), формирование хэш-кода по алгоритму SHA-1, симметричное шифрование на основе стандарта AES (Rijndail) и криптографическая защита передаваемых данных с помощью системы PGP 8.01.
Введение
При защите обрабатываемой, хранимой и передаваемой информации применяются математические вычисления, которые часто осуществляются над конечным множеством элементов. В качестве этих элементов могут быть биты, байты, слова, сообщения. Сообщения представляются последовательностью бит, байт. Элементы могут быть отображены в цифровом виде с конечным или бесконечным числом, а сами цифры в системах счисления с различным основанием. На практике наиболее часто используются системы счисления с основанием 2, 8, 10, 16.
|
|
Математические операции могут осуществляться с бесконечным или фиксированным числом различных элементов. В первом случае операции осуществляются над элементами бесконечного поля ("привычные" математические операции), а во втором - над элементами конечного поля, которые называют также полями Галуа [1,7].
Вычисления в конечных полях имеют свои особенности, и они нашли в частности широкое применение при защите информации. Поэтому приведем основные понятия и теоретические основы вычислений в конечных полях.
Структура полей Галуа связана со следующими определениями:
1) Коммутативная (абелева) группа: множество математических объектов, которые можно "складывать" и "вычитать".
2) Кольцо: множество математических объектов, которые можно "складывать", "вычитать" и "умножать".
3) Поле: множество математических объектов, которые можно "складывать", "вычитать", "умножать" и "делить".
Кавычки здесь обозначают, что это не обычные, но сходные с ними, арифметические операции.
Простейшее конечное поле состоит из двух элементов. Поле вещественных чисел содержит бесконечное число элементов. Если обозначить два элемента поля через 0 и 1, то операции умножения и сложения выглядят следующим образом:


Здесь Å - сложение по модулю 2.
Таким образом, полученные операции сложения и умножения называются сложением по модулю 2 и умножением по модулю 2.
Из равенства 1+1=0 следует, что  , а из равенства
, а из равенства 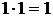 , что
, что  . Алфавит из двух символов 0 и 1 вместе со сложением и умножением по модулю 2 называется полем из двух элементов и обозначается через GF(2).
. Алфавит из двух символов 0 и 1 вместе со сложением и умножением по модулю 2 называется полем из двух элементов и обозначается через GF(2).
Понятие группы
Группой G называется множество элементов с определенной для каждой пары элементов операций (обозначаемой *), обладающее следующими 4 свойствами:
1) замкнутость: для каждой пары a и b из множества элементов  принадлежит множеству;
принадлежит множеству;
2) ассоциативность: для всех b и c из множества  ;
;
3) существование единицы: в множестве существует элемент, называемый единичным элементом e таким, что  для любого элемента a множества;
для любого элемента a множества;
4) существование обратных элементов: для любого a из множества существует некоторый элемент e из множества, называемый обратным элементу a и такой, что  .
.
Если группа G содержит конечное число элементов, то она называется конечной группой, а число элементов в G называется порядком G. Некоторые группы обладают дополнительным свойством: для любых a и b из группы  . Такое свойство называется коммутативностью, а группа - коммутативной или абелевой.
. Такое свойство называется коммутативностью, а группа - коммутативной или абелевой.
|
|
Есть много примеров групп, из которых многие содержат бесконечное число элементов. Примером могут служить целые числа относительно операции сложения, положительные числа относительно умножения. Примером группы является группа перестановок из символов. Пусть x представляет множество {1,2,..., n }. Взаимно однозначное отображение этого множества на само себя называется перестановкой. Всего имеется n! таких перестановок.
Возьмем n =5. Всего имеются 5!=120 перестановки в группе  . Типичный элемент группы
. Типичный элемент группы  равен
равен
a = [(12345)  (34152)]
(34152)]
и является перестановкой, заменяющей 1 на 2, 2 на 4, 3 на 1 и 4 на 3. Другой такой перестановкой является

Тогда произведение  в группе
в группе  равно перестановке, получающейся в результате применения сначала a, а затем b:
равно перестановке, получающейся в результате применения сначала a, а затем b:

что является элементом группы  . С таким определением умножения группа перестановок
. С таким определением умножения группа перестановок  является неабелевой.
является неабелевой.
Предположим, что G - группа, и пусть H - некоторое подмножество в G. Тогда Н называется подгруппой группы G, если Н является группой относительно ограничения операции на Н. Чтобы проверить, что непустое множество Н является подгруппой группы G, следует только проверить, что для всех a и b из Н элемент 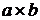 принадлежит Н (замкнутость) и что элемент, обратный к а из Н, также принадлежит Н. Остальные групповые свойства наследуются из группы G. Например, множество всех четных чисел и множество чисел, кратных 3, являются подгруппами в множестве всех целых чисел (положительных, отрицательных и 0) относительно операции сложения.
принадлежит Н (замкнутость) и что элемент, обратный к а из Н, также принадлежит Н. Остальные групповые свойства наследуются из группы G. Например, множество всех четных чисел и множество чисел, кратных 3, являются подгруппами в множестве всех целых чисел (положительных, отрицательных и 0) относительно операции сложения.
Конечные поля
Полем называется множество с двумя определенными на нем операциями - сложением и умножением, причем имеет место следующее:
1) Множество образует абелеву группу по сложению.
2) Поле замкнуто относительно умножения, и множество ненулевых элементов образует абелеву группу по умножению.
3) Закон дистрибутивности: (a + b)× c = a × c + b · c, для любых a, b и c из поля.
Единичный элемент относительно сложения принято обозначать через 0 и назвать нулем, аддитивный обратный элементу а элемент - через - а; единичный элемент относительно умножения - обозначать через 1 и называть единицей; мультипликативный обратный к элементу а элемент - через 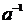 .
.
Примерами полей являются: множество вещественных чисел; множество комплексных чисел. Эти поля содержат бесконечное число элементов. Конечное поле или поле Галуа содержит конечное число q элементов и обозначается GF(q). Примером конечного поля является поле GF(7) = (0, 1, 2, 3, 4, 5, 6) для которого приведены таблицы 1.1 и 1.2 (сложения и умножения):
Таблица 1.1 Таблица 1.2
| · | + | ||||||||||||||||
В общем случае умножение и сложение в поле GF(7) не является умножением и сложением по модулю 7.
Операции в полях Галуа
Множество всех целых чисел образует кольцо относительно обычных операций сложения и умножения [1,7].
Целое число S делится на целое число r или r делит S, обозначается через r ÷ S (или r является делителем S), если r·a = S, где a – некоторое целое число. Если r делит S и делится на S, то r = ± S.
Положительное число p >1, которое делится только на ± p или ±1, называется простым числом. Число, не являющееся простым, называется составным. Простые числа, не превышающие 6000 приведены в приложении П.1.
Два числа называются взаимно простыми, если их НОД равен 1.
Как проверить, является ли число простым
Нет доступных и в то же время эффективных средств, позволяющих выяснить, является ли простым произвольное большое число. Один из наиболее удачных подходов к решению этой задачи алгоритм проверки целых чисел на простоту предложили Миллер (Miller) и Рабин (Rabin) [10]. Но сначала необходимо сформулировать определенные теоретические результаты, которые потребуются в дальнейшем. Вот первый из них.
Если р является нечетным простым числом, то уравнение
х 2 = 1 (mod p)
имеет только два решения: x º 1 и x º -1.
Пример. х2 º 1 (mod 7) х2 º 1 (mod 4)
Используем табл. 1.1, 1.2: Используем табл. 7.2(б):
12 º 1 mod 7, 12 º 1 mod 4,
62 º 36 mod 7º1 mod 7, 6 º-1 mod 7, 32 º 9 mod 4 º l mod 4,
Решения: 1; -1. Решения: 1; -1; 3; -3.
Алгоритм проверки целых чисел на простоту Миллера и Рабина основан на многократной проверке, имеет ли уравнение х 2 = 1 (mod p) при различных х решение, отличное от ± 1. Решение имеется только тогда, когда p не является простым.
Поиск наибольшего общего делителя
В кольце целых чисел важной операцией является операция деления. Для каждой пары целых чисел S и d при d ¹ 0 найдется единственная пара целых чисел а (частное) и r (остаток), таких, что
S = d× а + r, где 0 ≤ r < | d |. (1.1)
В теории вычислений больше интересует остаток, который можно записать в виде равенства:
r = Rd [ S ], (1.2)
которое читается так: r является остатком от деления S на d. Другое обозначение:
r = S (mod d). (1.3)
Остаток r часто называют вычетом числа S по модулю d.
Соотношение вида
A ≡ S (mod d) (1.4)
называется сравнением и читается так: S сравнимо с A по модулю d. Оно означает, что при делении чисел S и A на d получают один остаток, но не обязательно A < d.
Например, 24(mod 5) ≡ 34(mod 5).
По алгоритму деления можно найти НОД двух целых чисел.
Наибольший общий делитель двух целых чисел S и d НОД (S, d) определяется как наибольшее положительное число, которое делит оба из них. НОД можно найти по алгоритму Евклида, который выглядит следующим образом:
 (1.5)
(1.5)
Например, НОД (625, 65) находится так:
625 = 9 ´ 65 + 40,
65 = 1 ´ 40 + 25,
40 = 1 ´ 25 + 15,
25 = 1 ´ 15 + 10,
15 = 1 ´ 10 + 5,
10 = 2 ´ 5 + 0.
Следовательно, НОД (625,65) = 5.
Теперь можно выразить 5 в виде линейной комбинации чисел 625 и 65, начиная снизу выписанной выше последовательности:
5 = 15 – 1 ´ 10 = 15 – 1(25 – 1 ´ 15) = 2 ´ 15 – 1 ´ 25 =
= 2(40 – 1 ´ 25) – 1 ´ 25 = 2(625 – 9 ´ 65) – 3(65 – 1 ´ 40) =
= 2 ´ 625 – 25 ´ 65 + 3(625 – 9 ´ 65) = 5 ´ 625 – 48 ´ 65.
Таким образом, НОД (625,65) = 5 ´ 625 – 48 ´ 65.
Следовательно, для любых целых чисел S и существуют целые числа a и b, такие, что
НОД (S, d) = a × d + b × S. (1.6)
Данное равенство называется алгоритмом Евклида в общем виде.
Наименьшее общее кратное двух целых чисел S и d НОК (S, d) определяется как наименьшее положительное число, которое делится на оба из них. Наименьшее общее кратное можно подсчитать по следующей формуле:
 (1.7)
(1.7)
В классах вычетов
При сравнении по модулю n множество всех целых чисел отображается во множество Z n = {0, 1,..., (n - 1)}. При этом возникает вопрос: можно ли определить арифметические операции в рамках данного множества? Оказывается, можно, и соответствующий набор операций называется арифметикой в классах вычетов [6,10].
Операции арифметики в классах вычетов обладают следующими свойствами.
1. [(a mod n) + (b mod n)] mod п = (а + b) mod n.
2. [(а mod п) - (b mod n)] mod n = (а - b) mod п.
3. [(а mod п) × (b mod n)] mod n = (а × b) mod n.
Вот несколько примеров, иллюстрирующих указанные три свойства:
19 mod 8=3, 14 mod 8=6;
[(19 mod 8) + (14 mod 8)] mod 8 = 9 mod 8=1;
(19 + 14) mod 8 = 33 mod 8=1;
[(19 mod 8) - (14 mod 8)] mod 8 = - 3 mod 8=5;
(19 - 14) mod 8 = 4 mod 8=4;
[(19 mod 8) × (14 mod 8)] mod 8 = 18 mod 8=2;
(19 × 14) mod 8 = 266 mod 8=2.
Возведение в степень выполняется с помощью повторного умножения, как и в обычной арифметике.
Чтобы найти 117 mod 13, будем действовать следующим образом:
112 = 121 º4 mod 13,
114 º 42 º 3 mod 13,
117 º 11 × 4 × 3 º 132º 2 mod 13.
Итак, правила выполнения обычных арифметических операций — сложения, вычитания и умножения — можно применять и в арифметике классов вычетов.
Для арифметических операций по модулю п в этом множестве выполняются следующие свойства.
| Свойство | Выражение |
| Коммутативный закон | (x + y) mod n = (y + x) mod n (x × y) mod n = (y × x) mod n |
| Ассоциативный закон | [(x + y) +z)] mod n = [(x + (y + z)] mod n [(x × y) ×z)] mod n = [(x × (y × z)] mod n |
| Дистрибутивный закон | [(x × y) ×z)] mod n = [(x × y) × (y × z)] mod n |
| Тождества | (0+ y) mod n = y mod n (1× y) mod n = y mod n |
| Аддитивный обратный (- y) | Для любого y Î Z существует такое z, что (y + z) mod n ≡ 0 mod n |
Существует одна особенность арифметики в классах вычетов, которая делает ее отличной от обычной арифметики. Заметим сначала, что, как и в обычно арифметике, имеет место следующее свойство.
Если (а + b) º (а + с) mod п, то b º с mod п,(1.8)
(7 + 21) º (7 + 5) mod 8; 21 º 5 mod 8
Свойство (1.7) согласуется с существованием аддитивного обратного. Прибавив к обеим частям равенства (1.7) аддитивное обратное элемента а, получим ((- а) + а + b) = ((- a) + а + с) mod п, b º с mod п.
Однако следующее утверждение выполняется только при указанном ниже условии:
Если (а × b) º (а × с) mod п,то b º с mod п
при условии, что а и п взаимно просты. (1.9)
Рассмотрим пример, когда данное условие не выполнено:
4 × 3 = 12 º 4 mod 8,
4 × 5 = 20 º 4 mod 8.
Однако 3 ¹ 5 mod 8.
Операции над многочленами
Многочленом над полем GF(q) называется математическое выражение:
 , (1.10)
, (1.10)
где х - называется фиктивной переменной, коэффициенты fn- 1, fn- 2,…, f 0 принадлежат полю GF(q), а показатели степеней являются целыми числами.
Нулевым многочленом называется многочлен f (x) = 0.
Приведенными многочленами называются многочлены, старший коэффициент которых fn- 1 = 1. Степенью ненулевого многочлена f (x), которая обозначается deg f (x), называется индекс старшего коэффициента fn- 1.
Множество всех многочленов над полем GF(q) образует кольцо относительно сложения и умножения, определяемых по обычным принципам сложения и умножения многочленов. Такое полиномиальное кольцо можно определить для каждого поля Галуа GF(q). Такое кольцо обозначается GF(q)[ x ]. Элементы кольца GF(q) называют скалярами.
Суммой двух многочленов f (x)и q (x) из GF(q)[ x ] называется многочлен из GF(q)[ x ], определяемый равенством:
 . (1.11)
. (1.11)
Например, для поля GF(2)
(х 4 + х 2 + х +1)+(х 5 + х 4 + х 3 +1)=
= х 5 +(1Å1) х 4 + х 3 + х 2 + х +(1Å1)=
= х 5 + х 3 + х 2 + х.
Произведением двух многочленов из GF(q)[ x ] называется многочлен, определяемый равенством:
 . (1.12)
. (1.12)
Например, над GF(2)
(х 4 + х 2 +1)×(х 2 +1)= х 6 +1
Кольцо многочленов во многих отношениях соответствует кольцу целых чисел. Многочлен S (x) делится на многочлен d (x), если существует многочлен a (x), такой, что
d (x) × a (x) = S (x).
Многочлен p (x) делящийся на многочлен a× p (x) или a, называется неприводимым многочленом, где a – произвольный ненулевой элемент поля GF(q). Приведенный неприводимый многочлен называется простым многочленом.
Если S (x) одновременно делится на d (x) и делит d (x), то
S (x) = a× d (x).
Для каждой пары многочленов S (x) и d (x) (при d (x)¹ 0) существует единственная пара многочленов a (x) (частное) и r (x) (остаток), таких, что
S (x) = d (x) × a (x) + r (x), (1.13)
где deg S (x) < deg d (x).
Практическое вычисление частного и остатка осуществляется по обычным правилам деления многочленов. В теории кодирования большое значение имеет остаток. Остаток можно записать в виде:
r (x) = R d ( x )[ S (x)]. (1.14)
Часто остаток называется вычетом многочлена S (x) по модулю многочлена d (x).
r (x) = S (x)[mod d (x)], (1.15)
Несколько отличным понятием является сравнение, которое означает, что при делении на d (x) многочлены S (x)и A (x) дают один и тот же остаток, но deg A (x) необязательно меньше deg d (x).
A (x) ≡ S (x)[mod d (x)], (1.16)
Ненулевой многочлен p (x) над некоторым полем однозначно разлагается в произведение элемента поля и простых многочленов над этим полем.
Наибольший общий делитель двух многочленов S (x) и d (x)
НОД [ S (x), d (x)] определяется как приведенный многочлен наибольшей степени, делящий одновременно оба из них. Если НОД [ S (x), d (x)] = 1, то они называются взаимно простыми.
Наибольший общий делитель двух многочленов S (x) и d (x) над полем GF(q) можно вычислить с помощью итеративного алгоритма деления Евклида. Если deg S (x) ³ deg d (x) ³ 0, то последовательность вычислений такова:

 . (1.16)
. (1.16)
Процесс обрывается, как только будет получен нулевой остаток.
Наибольший общий делитель двух многочленов S (x) и d (x) на основе алгоритма в общем виде (аналогично целым числам) можно записать в виде:
НОД [ S (x), d (x)] = a (x) × d (x) + b (x) × S (x), (1.17)
где a (x) и b (x) многочлены над GF(q), которые можно найти из представленной выше системы уравнений (1.16).
Наименьшее общее кратное двух многочленов S (x) и d (x)
НОК[ S (x), d (x)] определяется как приведенный многочлен наименьшей степени, делящийся на оба из них. Значение НОК можно вычислить по формуле:
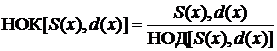 . (1.18)
. (1.18)
Для произвольного элемента b из GF(q) можно вычислить значение многочлена над GF(q) в этой точке, подставив элемент b вместо x. Например, в поле GF(3), (q ={0,1,2})
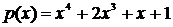 .
.
Тогда
 .
.
Можно вычислить значение многочлена над GF(q) в расширении поля GF(q). Это вычисление проводится подстановкой элементов из расширения поля вместо фиктивной переменной х и выполнением операций в расширении поля. Например, пусть GF(2)
 .
.
Пусть для элементов поля GF(4) имеем следующие правила сложения и умножения:
Таблица 1.3 Таблица 1.4
| · | + | ||||||||||||
Тогда
 .
.
Если р (b) = 0, то элемент b называется корнем многочлена р (х).
Многочлен необязательно имеет корни в собственном поле. Многочлен  не имеет корней в GF(2), но имеет корень в расширении поля, т. е. в GF(4).
не имеет корней в GF(2), но имеет корень в расширении поля, т. е. в GF(4).
Элемент b является корнем многочлена р (х) тогда и только тогда, когда (x-b) делит р (х). У р (х) степени n не более n корней.
Конечных полей
Введение
Один из методов генерации ключей основан на теории конечных полей. Средства генерации конечных полей за цикл длиной qn вырабатывают qn-1 различных последовательностей (элементов) без их повторения, где q – характеристика поля (основание системы счисления), n - степень расширения поля [3,7]. Последовательности, вырабатываемые согласно теории конечных полей, являются псевдослучайными (они не вырабатывают нулевой элемент), также при генерации ключей для шифрования случайный их характер является одним из основных требований, обеспечивающим необходимую стойкость шифра. Стойкость криптографической системы увеличивается с увеличением длины последовательности и степени их случайности. Рассмотрим методику генерации псевдослучайных элементов конечных полей.
Таблица 2.2
| + | х | х +1 | ||
| x x +1 | x x +1 | x +1 x | х x +1 | х +1 х |
Таблица 2.3
| * | х | х +1 | ||
| х х +1 | х х +1 | х х +1 | х +1 х |
Примитивные элементы
Примитивным элементом поля GF(q) называется такой элемент a, что все элементы поля, за исключением 0, могут быть представлены в виде степени элемента a. Например, в поле GF(5) = 2, 21=2, 22=4, 23=3, 24=1, так что 2 является примитивным элементом поля GF(5). Примитивные элементы полезны при построении полей, если один из них найден, то, перемножая степени этого примитивного элемента, можно составить таблицу умножения в поле. Каждое поле содержит примитивный элемент.
Пусть b 1, b 2,…, bq- 1 ненулевые элементы поля GF(q), тогда
хq- 1-1 = (x - b 1)×(x - b 2)…(x - bq- 1),
и пусть b - какой-либо ненулевой элемент из GF(q), тогда
bq- 1 = (b - b 1)×(b - b 2)…(b - bq- 1) = 1
Тогда b является корнем многочлена xq- 1-1.
Группа ненулевых элементов поля GF(q) по умножению является циклической. Для простого q- 1 это тривиально, так как порядок всех элементов, за исключением 0 и 1 равен q- 1, так что каждый элемент примитивен. В каждом поле Галуа имеется примитивный элемент [7].
Структура конечного поля
С помощью примитивного элемента можно построить поле Галуа. Например, в поле GF(8) порядок каждого ненулевого элемента равен 7 или делит на 7, так как 7 – простое число. Поэтому каждый ненулевой элемент является примитивным. Поле GF(8) можно построить с помощью многочлена
p (x) = x 3 +x 2 + 1. Другие неприводимые многочлены приведены в таблице приложения 2. Основываясь на примитивном элементе a, который является корнем p (x)получим:
a = x 1 = 010,
a 2 = x 2 = 100,
a 3 = x 2 + 1 = 101,
a 4 = x 2 + x+ 1 = 111,
a 5 = x+ 1 = 011,
a 6 = x 2 + x = 110,
a 7 = a 0= x 0  = 001.
= 001.
В таком представлении умножение и сложение выполняется легко. Например,
a 5 × a 6 = a 4, a 5 + a 6 = a 3.
При построении расширения поля в виде множества многочленов удоб-но, чтобы примитивному многочлену соответствовал примитивный элемент поля. Тогда построение поля можно осуществлять с помощью простых многочленов, называемых примитивными. Примитивным многочлен p (x)над полем GF(q) называется простой многочлен над GF(q), такой, что в расширении поля, построенным по модулю p (x),соответствующему многочлену, элемент поля является примитивным. Для каждого поля существуют примитивные многочлены всех степеней [7].
Число элементов наименьшего подполя поля GF(q) называется характеристикой поля GF(q). Каждое поле Галуа содержит единственное наименьшее подполе, число элементов которого равно простому числу. Следовательно, характеристика каждого поля Галуа является простым числом. Например, для GF(32) наименьшее подполье GF(2) содержит два элемента.
В поле Галуа GF(q) можно построить подполе GF(p), где p – простое число. В частности, если q является простым числом, то поле GF(q) можно интерпретировать как поле чисел по модулю q. Следовательно, для заданного простого числа существует только одно поле с заданным числом элементов, хотя оно может быть представлено разными способами. Два поля, отличающиеся только представлениями, называются изоморфными.
Пусть GF(q) – некоторое поле, пусть GF(Q) – расширение поля GF(q) и пусть b - элемент GF(Q). Простой многочлен f (x) наименьшей степени над GF(q), для которого f (b) = 0, называется минимальным многочленом элемента b над GF(q). Каждый элемент b из GF(Q) имеет единственный минимальный многочлен над GF(q). Если минимальный элемент многочлена f (x) равен b и b является корнем многочлена g (x), то f (x) делит g (x).
Элемент b является всегда корнем многочлена xQ - x, который разлагается на простые многочлены над полем GF(q):
хQ – x = f 1(x) × f 2(x) …fk (x).
Если Q = qm, то каждый делитель многочлена x  - x, неприводимый над полем GF(q), имеет степень равную m или меньшую.
- x, неприводимый над полем GF(q), имеет степень равную m или меньшую.
При Q = q разложение сводится к равенству:
хq

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!