Способ параллельного переноса

Параллельный перенос представляет собой перемещение геометрической фигуры параллельно одной из плоскостей проекций. При этом величина проекции фигуры на эту плоскость не меняется. Например, если перемещать отрезок EF параллельно горизонтальной плоскости П₁, то длина его проекции E'F' не изменится, когда она займет новое положение E'₁F'₁.

Еще одно важное свойство параллельного переноса заключается в том, что при любом перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. Если точка перемещается параллельно фронтальной плоскости, то её горизонтальная проекция движется по прямой, параллельной оси X.

 

10.Определение натуральной величины плоской фигуры методами проецирования на дополнительную плоскость.

Во-первых, решим эту задачу способом замены плоскостей проекций (рис.9). Для этого:

1) проведем в плоскости треугольника АВС фронталь f (линия С -1), а затем, заменяя π₁, введем новую плоскость проекций π₃, проходящую через ось Х ₁ и перпендикулярную к фронтальной проекции фронтали f" (С "-I"). На π₃ заданная плоскость треугольника АВС спроецируется в прямую линию, т.е., станет проецирующей по отношению к этой плоскости проекций;

2) второй заменой плоскости проекций π₂ на новую плоскость проекций π₄, проходящую через ось Х ₂ и параллельную проекции А"′В "′ С "′ нашего треугольника, найдем на плоскости π₄ натуральную величину треугольника ABС - фигуру А ^1V В ^1V С ^1V.

 

11.Наклонные сечения многогранников.

 

Первоначально строят горизонтальную проекцию фигуры сечения (рис. 218). Эта проекция является вспомогательной, она не дает действительной величины фигуры сечения, но позволяет безошибочно построить заданное сечение. Затем на произвольном расстоянии проводят ось симметрии фигуры сечения параллельно прямой А—А и в обе стороны от нее по перпендикулярному направлению откладывают величины, взятые с горизонтальной проекции фигуры сечения. На чертеже показано построение крайних отрезков а и b. На окончательном чертеже сохраняют только верхнее сечение — действительную форму фигуры сечения. При несимметричных сечениях вводят оси проекций х₁₂ и s₂₄ или другие, в зависимости от того, какую плоскость заменяют.

Для изучения разрезов и сечений часто применяют полые модели с проходными отверстиями. Решение подобных задач очень ценно не только для освоения разрезов и сечений, но и для развития пространственных представлений. Ценность задач увеличивается в связи с тем, что многие из них напоминают примеры из машиностроительной практики. Особенно часто встречаются в практике отверстия в пустотелых корпусах цилиндрической, конической и сферической форм.

 

 

12.Наклонные сечения тел вращения.

Известно, что некоторые наклонные сечения тел вращения, особенно тех, которые нашли широкое применение в инженерной практике, ограничены закономерными кривыми линиями (окружностями, эллипсами, гиперболами и т.п.). Для построения таких линий существуют способы и приемы их наиболее точного и простого воспроизведения. Поэтому графической работе по выполнению сечений должен предшествовать анализ как самой формы рассекаемой фигуры наклонного сечения, так и способа ее построения. Это помогает избежать ошибок и неточностей при выполнении и чтении чертежей.

8.2.1. Наклонные сечения цилиндра

Выше было рассмотрено образование цилиндрической поверхности с помощью образующей - прямой линии и направляющей - окружности. Поэтому, если секущая плоскость будет проходить через образующие, то в сечении получим параллельные прямые, если через направляющие, то - окружность. Все остальные сечения цилиндра будут эллипсами. Построение сечения цилиндра фронтально проецирующей плоскостью рассмотрено на рис. 8.2.

Рис. 8.2.

 

Так как секущая плоскость перпендикулярна фронтальной плоскости проекций.то фронтальная проекция линии пересечения на чертеже имеется. Она совпадает с фронтальной проекций плоскости. В свою очередь, поверхность цилиндра перпендикулярна горизонтальной плоскости проекций. Следовательно, горизонтальная проекция линии пересечения совпадает с горизонтальной проекций цилиндра.

Натуральную величину сечения построим по точкам. Отметим на чертеже точки, соответствующие большой АВ и малой CD осям эллипса.

Так как секущая плоскость перпендикулярна фронтальной плоскости проекций, то и новая плоскость П₄ ^ П₂. Новая ось будет параллельна фронтальной проекции секущей плоскости. Чтобы линии связи не пересекали горизонтальную проекцию, наклонное сечение можно сместить по оси х₁. При построении следует учитывать, что линии связи отсекают на оси х₁ и на фронтальной проекции секущей плоскости отрезки, равные друг другу.

В связи с этим в любом месте на оси х₁ откладываем большую ось эллипса. Через середину полученного отрезка проводим линию связи, перпендикулярную х₁, и стороим точки, соответствующие малой оси эллипса.

Для построение эллипса необходимо также несколько промежуточных точек. Обозначаем их на П₂ и находим на П₁. Затем измеряем расстояние А₂1₂ и откладываем его по х₁ от А₄, проводим линии связи и откладываем координаты Y точек 1 и 2. Остальные точки строим аналогично. Соединив полученные точки с помощью лекала, получим натуральную величину наклонного сечения цилиндра.

 

8.2.2. Наклонные сечения конуса

Рассмотрим сечения прямого кругового конуса (рис. 8.3). Если секущая плоскость будет проходить через образующую (прямую), то в сечении получим треугольник, если через направляющую (окружность) - окружность.

Рис. 8.3.

 

Все остальные сечения кругового конуса будут лекальными кривыми второго порядка, а именно: - эллипсом, когда секущая плоскость пересекает все образующие конуса; - параболой - секущая плоскость параллельна одной из образующих; - гиперболой - секущая плоскость параллельна двум образующим.

В связи с этим работа по выполнению наклонного сечения конуса начинается с анализа положения секущей плоскости относительно оси вращения и образующих конуса. И лишь после установления характера получаемой линии проводится графическое построение ее проекций.

На рис. 8.4 выполнен чертеж конуса, и показана секущая плоскость Б-Б, которая пересекает все образующие данного конуса. Следовательно, фигура сечения будет ограничена эллипсом, а отрезок А₂B₂ является его фронтальной проекцией.

Рис. 8.4.

 

Натуральную величину сечения можно построить по законам построения эллипса. Для этого на оси х откладываем большую ось эллипса АВ и малую CD. Причем, малая ось эллипса определяется как хорда (CD) параллели, делящей пополам фронтальную проекцию сечения.

Построение сечения конуса плоскостью параллельной одной образующей конуса рассмотрено на рис. 8.5. Секущая плоскость перпендикулярна профильной плоскости проекций. Построены горизонтальная и фронтальная проекции и натуральная величина сечения, которое ограничено параболой.

При построении наклонного сечения цилиндра было показано, что натуральную величину сечения можно сместить вдоль оси х₁ При этом линии связи отсекают на оси х₁ и на секущей плоскости равные отрезки. Если ось х₁ повернуть относительно секущей плоскости, например, расположить горизонтально, то линии связи на оси х₁ и на секущей плоскости также будут отсекать равные отрезки. Так как секущая плоскость перпендикулярна П₃, следовательно новая плоскость П₄ также перпендикулярна П₃. Поэтому вдоль линий связи необходимо откладывать координаты Х соответствующих точек.

Построение и сечение конуса плоскостью параллельной двум образующим приведено на рис. 8.6. Фигура сечения ограничена гиперболой. Построение аналогично построению точек на рис. 8.5.

Рис. 8.5.

Рис. 8.6.

 

8.2.3. Наклонные сечения шара

 

Как известно, любое сечение шара плоскостью является кругом. В зависимости от положения секущей плоскости, окружность, ограничивающая фигуру сечения, может спроецироваться в:
- окружность, если секущая плоскость параллельна плоскости проекций;
- отрезок прямой, если секущая плоскость перпендикулярна плоскости проекций;
- эллипс, если секущая плоскость наклонена к плоскости проекций.

Рис. 8.7.

Так как сечение шара - круг (рис. 8.7), то построение его натуральной величины сводится к определению радиуса окружности. Участок линии сечения А₃В₃ является диаметром этой окружности. Поэтому для построений на новую ось х₁ линиями связи переносятся точки О и В, после чего радиусом, равным расстоянию между ними, проводится окружность - граница фигуры сечения А-А.

При построении проекций сечения на видах вначале построены точки эллипса на главном виде. Так точки А и В находятся на пересечении горизонтальных линий связи с вертикальной центровой линией шара (проекцией главного профильного меридиана). Точки С и D, принадлежащие второй оси эллипса, построены с помощью окружности а, параллельной фронтальной плоскости проекций. На главном фронтальном меридиане расположены точки Е и F, поэтому их фронтальные проекции легко строятся по линии связи. Точки К и L принадлежат экватору. Вначале удобно построить горизонтальные проекции этих точек, а затем по линиям связи найти фронтальные.

Положение точек сечения на виде сверху определяется с помощью линий связи, вдоль которых откладываются координаты Y соответствующих точек. При завершении чертежа полученные на видах проекции точек соединяются при помощи лекала, а сечение и его проекции заштриховываются.

 

13.Линии среза.

ЛИНИИ СРЕЗА

Среди линий перехода есть такие (рис.9.1, линия 1), которые образованы отсечением части тела вращения плоскостью, параллельной оси вращения. Их принято называть линиями среза.

При выполнении чертежей тел, содержащих линии среза,тела обычно располагают так, чтобы плоскость среза, а следовательно, и линия среза были параллельны фронтальной плоскости проекций. При таком расположении проекция линии среза на главном виде будет иметь натуральный вид, а на видах слева и сверху ее проекциями окажутся отрезки прямых - следы секущих плоскостей (рис. 9.6).

Рис. 9.6.

 

При построении проекций линии среза точки А₃, В₃ и симметричные им точки А₃', В₃' рассматриваются как известные профильные проекции характерных точек. Проекции указанных точек на главном виде находятся на пересечении линий связи с фронтальными проекциями параллелей, проведенных через эти точки. Так, проекции самой высшей точки А и самой низшей А' построены на проекции экватора, проекции точек В и В' (крайние левая и правая) на проекции параллели касательной к плоскости среза.

При построении проекций промежуточных точек 1 и 2, вначале через профильные проекции этих точек проводятся проекции параллелей с и d. Положение проекций параллелей на главном виде определяется пересечением линий связи с главным фронтальным меридианом поверхности вращения. В свою очередь, фронтальные проекции точек 1 и 2 и симметричных им 1' и 2' находятся на пересечении линий связи того же направления с фронтальными проекциями параллелей.

Завершают чертеж соединением полученных проекций характерных и промежуточных точек плавной лекальной кривой.

14.Пересечение многогранников.

При пересечении поверхностей многогранников может быть два случая:
а) Полное внутреннее пересечение (фиг.329,а);
б) Частичное пересечение (фиг.329,б).

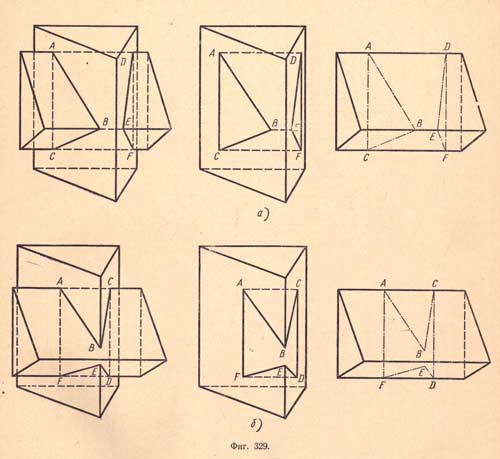
При полном внутреннем пересечении поверхность одного многогранника как бы пронзит поверхность другого многогранника, при этом получатся две замкнутые ломаные линии пересечения (АВСА и EDFE).

При частичном пересечении обе поверхности многогранников как бы врезаются одна в другую и у каждой из них, естественно, остаются какие - либо, непересеченные ребра; при этом получается только одна замкнутая ломаная линия пересечения (ABCDEFA).

Линию пересечения двух многогранников обычно определяют по точкам пересечения ребер одного многогранника с гранями другого и ребер второго с гранями первого (способ пересечения прямой с поверхностью тела). Найденные точки соединяют в последовательном порядке и получают линию пересечения.

Видимыми частями линии пересечения будут те, которые принадлежат видимым на этой проекции граням обоих многогранников. Если же в какой - нибудь проекции хотя бы одна из граней будет невидима, то в этой проекции и линия пересечения, лежащая на указанной грани, будет невидимой.

15.Построение линий пересечения тел вращения методом секущих плоскостей.

Вкратце суть метода секущих плоскостей состоит в том, что для построения линии пересечения двух поверхностей строятся вспомогательные плоскости (обычно – параллельные одной из плоскостей проекций), которые пересекают заданные поверхности, образуя при этом простые геометрические фигуры. Точки взаимного пересечения заданных поверхностей будут общими точками двух кривых, образованных пересечением секущей плоскости с каждой из поверхностей. Очевидно, что для тел вращения удобно использовать плоскости, перпендикулярные осям этих тел. В нашем случае вспомогательные плоскости будут параллельными горизонтальной плоскости. Изобразим их на фронтальном виде (в нашем случае верхняя из плоскостей проходит через явно видимую верхнюю точку пересечения конуса и полусферы, в других случаях для нахождения этой точки потребуются дополнительные построения):

Теперь перенесем линии пересечения секущих плоскостей с каждой из поверхностей на вид сверху. Очевидно, что горизонтальные плоскости пересекают каждое из тел по окружностям, центры которых находятся на одной вертикали с центрами тел. Радиусы этих окружностей легко переносятся на вид сверху с образующих каждой поверхности. Вот эти окружности для полусферы:

И для конуса:

3. Отметим для наглядности общие точки для каждой из пар окружностей, образованных одной плоскостью:

Вот еще две точки, заданные этой плоскостью:

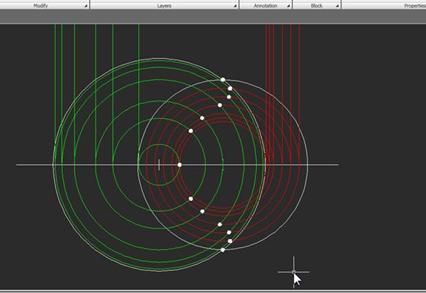
Соединив на виде сверху полученные точки мы получим приближенную линию пересечения двух поверхностей:

4. Остается перенести линию на фронтальный вид. Сделать это совсем несложно: нужно перенести каждую из точек с вида сверху на соответствующую секущую плоскость на фронтальном виде. Линии построения выделены желтым цветом:

Поскольку исходные поверхности (и, соответственно, линия их пересечения) симметричны относительно плоскости, параллельной фронтальной плоскости проекции, достаточно перенести только половину точек. В нашем частном случае невидимая на фронтальном виде часть кривой «спрятана» за видимой, а верхняя точка является точкой разделения видимой и невидимой частей.

 

16. Построение линий пересечения тел вращения методом секущих сфер.

Способ вспомогательных секущих сферических поверхностей позволяет определять линию пересечения двух произвольных поверхностей вращения.
Для этого используется свойство присущее поверхностям вращения - две любые соосные поверхности вращения пересекаются по окружности, проходящей через точки (A, B) пересечения их меридианов (m1, m2).

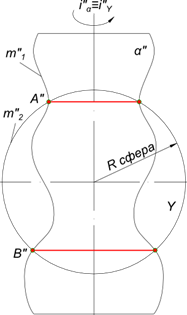
Способ вспомогательных секущих сферических поверхностей

Плоскости окружностей сечения перпендикулярны оси поверхности вращения. Поэтому, если оси поверхностей вращения параллельны плоскости проекции, то на эту плоскость окружности сечения проецируются в отрезки прямых, перпендикулярных проекции на нее оси вращения.
В качестве вспомогательной секущей поверхности вращения используют удобную для вычерчивания сферическую поверхность, центр которой должен принадлежать оси поверхности вращения.
Задачи по определению линии пересечения двух произвольных поверхностей вращения, имеющих общую плоскость симметрии просто решаются с помощью вспомогательных сферических поверхностей.
При этом различают два случая:
- если оси поверхностей пересекаются;
- если оси поверхностей не пересекаются.

Оси двух произвольных поверхностей вращения пересекаются

Способ вспомогательных секущих сферических поверхностей

определение линии пересечения двух поверхностей вращения выполняют с помощью концентрических сфер.
В данном примере это конус и тороид (самопересекающийся тор),
используется способ вспомогательных секущих сферических поверхностей, которые имеют общий центр.
Применение концентричных сфер возможно при наличии трех графических условий:
- пересекаются поверхности вращения (за исключеним открытого и закрытого тора);
- общая плоскость симметрии представляет собой плоскость уровня;
- оси поверхостей пересекаются в точке, которая служит общим центром вспомогательных секущих сферических поверхностей.
Способ вспомогательных секщих плоскостей тут применять не рационально, так как ни одна плоскость уровня не пересекает поверхности по окружностям.
Алгоритм построения линии пересечения:
- находим опорные точки A и B, C и D в пересечении меридиональных сечений m1 и m2 поверхностей α и β;
- находим точку пересечения осей поверхностей α и β: О=(iα ∩ iβ);
- проводим вспомогательную сферическую поверхность Y произвольным радиусом Р, которая пересечет пересечет поверхности α и β по окружностям a=(α ∩ Y) и b=(β ∩ Y) соответственно;
- находим точки линии пересечения в пересечении окружностей;
- действуя подобным образом, можно найти достаточное количество точек, соединив которые плавной линией получим искомую линию пересечения поверхностей.

Когда оси поверхностей не пересекаются

Способ вспомогательных секущих сферических поверхностей

Построение линии пересечения открытого тора и цилиндра выполняется способом эксцентричных сфер так как:
- открытый тор имеет круговые сечения во фронтально-проецирующих плоскостях, проходящих через его ось вращения i_t;
- общая плоскость симметрии поверхностей;
- оси поверхностей скрещиваются

и ведется по следующему алгоритму:
- вводим вспомогательные сферы, задавая произвольные сечения поверхности тора фронтально проецирующими плоскостями, проходящими через его ось. Окружность a1-a2 - это заданная линия пересечения тора с искомой вспомогатнльной сферой, центр которой должен лежать на перпендикуляре к проекции этой окружности;
- проводим к прямой a1-a2 через ее середину перпендикуляр к и на его пересечении с осью цилиндра находим центр O1 вспомогательной сферы;
- из центра O1 проводим окружность радиусом Rсф1;
- строим линию пересечения сф1 с цилиндром b1-b2;
- в пересечении a1-a2 и b1-b2 находим совпадающие точки 1(1);
- действуя подобным образом, можно найти достаточное количество точек, соединив которые плавной линией получим искомую линию пересечения поверхностей.

17.Теорема Монжа.

Особые случаи пересечения. Теорема Монжа

1. Поверхности в точках касания имеют общие касательные плоскости.

Теорема (о двойном соприкосновении).

Если две поверхности второго порядка имеют две точки соприкосновения и общие касательные плоскости в этих точках, то линия их пересечения распадается на две плоские кривые второго порядка.

Сфера и эллиптический цилиндр пересекаются по двум окружностям. Они имеют две общие точки А и В и две общие касательные плоскости в этих точках. Пространственная линия пересечения распалась на две плоские кривые – окружности(рис. 159).

Рис. 152

2. Две пересекающиеся поверхности касаются третьей поверхности второго порядка.

Теорема (теорема Г.Монжа).

Если две пересекающиеся поверхности второго порядка могут быть описаны вокруг третьей поверхности второго порядка или вписаны в нее, то они пересекаются по двум плоским кривым второго порядка.

Теорема Монжа – частный случай теоремы о двойном соприкосновении. Например, поверхности конуса и цилиндра с общей фронтальной плоскостью симметрии касаются сферы по окружностям 1”-2”и 3”-4”. Линия пересечения поверхностей представляет собой два эллипса, плоскости которых перпендикулярны фронтальной плоскости проекций(рис. 160).

Рис. 153

На рис. 161 даны два конуса, описанные вокруг одного и того же шара. Оси которых пересекаются под прямым углом. Построить линию пересечения заданных поверхностей.

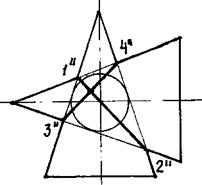
Рис. 154

Наивысшие 1, 3 и наинизшие 2, 4 точки линии перехода находят в пересечении крайних образующих на фронтальной проекции заданных поверхностей. Если сфера касается обеих поверхностей, то линия их пересечения распадается на две плоские кривые (в нашем примере – на два различных эллипса). На фронтальной проекции эти эллипсы изображаются отрезками прямых, а на горизонтальной – эллипсами.

Точки 5 и 6 пересечения эллипсов находят на окружности радиуса c”/2. Построение промежуточных точек ясно из чертежа.

Для определения видимости линий пересечения на горизонтальной проекции проводят секущую плоскость Р (через ось конуса с вершиной S). Точки 7, 8 и 9, 10 служат границами раздела между видимой и невидимой частями линий пересечения. На фронтальной проекции невидимая часть линии пересечения сливается с видимой.

Прямые 1-4 и 2-3 – большие оси эллипсов. Прямые 5-6 и 11-12 -- малые оси эллипсов.

На рис. 162 даны два цилиндра с одинаковыми диаметрами. Оси цилиндров пересекаются под прямым углом.

Здесь в пересечении цилиндров получаются два одинаковых эллипса 1-2 и 3-4, которые проецируются на плоскость V в виде прямых, а на плоскость Н – в виде окружностей, сливающихся с проекцией основания одного из цилиндров.

Рис. 155

18.Поверхности с двумя направляющими и плоскостью параллелизма.Определитель поверхности.

Определитель поверхности состоит из двух частей: геометрической и алгоритмической.

В геометрическую часть определителя входят геометрические фигуры и отношения между ними. В алгоритмическую часть - закон образования поверхности.

Чтобы отличить геометрическую часть определителя от алгоритмической, первую заключают в круглые скобки, а вторую - в квадратные. Тогда определитель произвольной поверхности будет иметь следующую форму:

Ф (Г)[А],

где (Г) - геометрическая часть; [А] - алгоритмическая часть.

 

Эти поверхности образуются движением прямолинейной образующей по двум направляющим. Образующая во время своего движения все время остается параллельной некоторой плоскости, называемой плоскостью параллелизма. Определитель: Ф(l, a, b) [l½½Г].

Косая плоскость

Если направляющими служат две скрещивающиеся прямые, а прямолинейная образующая движется по этим направляющим, оставаясь все время параллельной плоскости параллелизма, то полученную поверхность называют косой плоскостью или гиперболическим параболоидом (рис.3.20-а).

Рис. 3.20

 

На рис.3.20-б показана косая плоскость, для которой направляющими служат две скрещивающиеся прямые а и b, а в качестве плоскости параллелизма принята горизонтальная плоскость проекций П₁. Определитель: Ф(l, a Æ b)[l½½П₁].

Цилиндроид

Поверхность цилиндроида можно получить, приняв за направляющие две непараллельные и не лежащие в одной плоскости кривые k и t. Образующая во всех своих положениях скользит по этим направляющим, оставаясь все время параллельной плоскости параллелизма, например П₂ (рис.3.21). Определитель: Ф(l, k, t) [l½½П₂].

Рис. 3.21

Коноид
Коноид получается при движении образующей по двум направляющим, не лежащим в одной плоскости, одна из которых является прямой, вторая - кривой. На рис.3.22 показана такая поверхность. За плоскость параллелизма принята плоскость Г. Определитель: Ф(l, a, k) [l½½Г].

Рис. 3.22

19.Определение натуральной величины отрезка методом вращения.

Отрезок, параллельный какой-нибудь плоскости проекций, проецируется на нее без искажения. Если повернуть отрезок таким образом, чтобы он стал параллельным одной из плоскостей проекций, то можно определить его натуральные размеры. Это вращение осуществляется легче всего вокруг оси, которая перпендикулярна одной из плоскостей проекций.

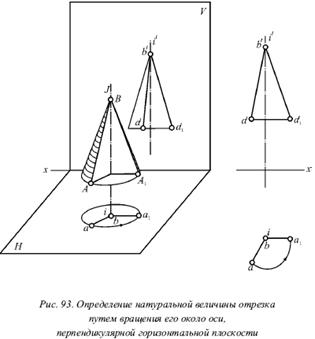
На рисунке 93 показано вращение отрезка около оси, которая перпендикулярна горизонтальной плоскости. Пусть дан произвольный отрезок АВ, тогда проведем через точку В вертикальную прямую I. Она, в свою очередь, перпендикулярна горизонтальной плоскости. Теперь будем вращать отрезок АВ около этой прямой I. При этом отрезок АВ опишет поверхность прямого кругового конуса, а его вершина будет расположена в точке В (рис. 93). Прямая I здесь является осью конуса. В этом случае точка А описывает окружность, которая является основанием этого конуса. Данное основание изображается в натуральную величину на горизонтальной плоскости, в виде отрезка, параллельного оси х, на фронтальной плоскости. Отрезок АВ представляет собой образующую конуса.

Отрезок АВ будем вращать до тех пор, пока он не расположится параллельно фронтальной плоскости (таких положений будет два, и они совпадают на фронтальной плоскости с контуром вспомогательного конуса). В этом случае его горизонтальная проекция должна стать параллельной оси х. Оказалось, что точка В легла на ось вращения, поэтому при вращении отрезка она не изменит своего положения. На рисунке 93 показано, как горизонтальная проекция а описывает дугу окружности с центром в точке b, а фронтальная проекция а перемещается по прямой, параллельной оси х.

Проекция является натуральным изображением отрезка АВ, т. е. a? ₁ b? = AB.

На рисунке 94 показано вращение отрезка около оси, которая перпендикулярна фронтальной плоскости. При этом натуральная величина отрезка АВ установлена вращением около оси I, которая проходит через точку В перпендикулярно фронтальной плоскости. В этом случае построение абсолютно аналогично тому, которое было рассмотрено ранее.

20.Винтовые линии.

Винтовая линия относится к пространственным кривым. Различают цилиндрические, конические, сферические и другие винтовые линии.

Цилиндрическая винтовая линия описывается точкой, которая совершает равномерное движение вдоль образующей кругового цилиндра, а образующая вращается с постоянной угловой скоростью вокруг оси цилиндра.

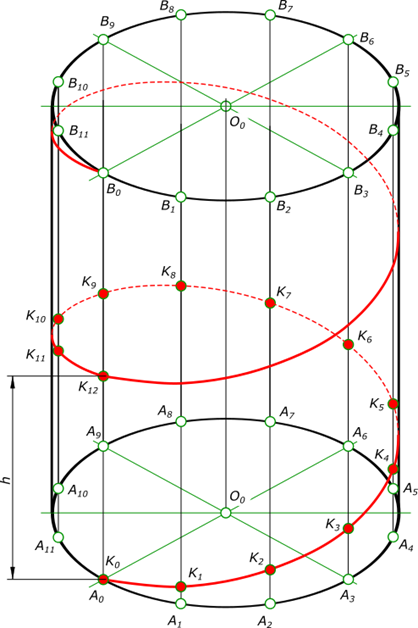
Винтовая линия

Образующая занимает 12 последовательных положений: A⁰B⁰.
Дуги A⁰A¹, A¹A² A²A³ и т. д. равны между собой и каждая равна pd/n, где d - диаметр цилиндра, p = 3,14 и n - число положений образующей цилиндра, принятое для построения. Пусть образующая занимает 12 последовательных положений: A⁰B⁰, A¹B¹, A²B² и т. д.
Начальному положению образующей AB соответствует A⁰B⁰, а точки K - K⁰.
При перемещении образующей AB в положение A¹B¹ точка K займет положение K¹, и поднимется по образующей на величину отрезка A¹K¹ = h/12. При последующем перемещении образующая займет положение A²B², а точка K положение K² и поднимется на высоту равную A²B² = 2A¹B¹ = 2(h/12), и т. д. Когда образующая совершит полный оборот и снова займет начальное положение, точка K будет находится на ней на высоте A¹²B¹² = 12(h/12) = h, величине шага винтовой линии. При этом точка описывает кривую K⁰K⁶K¹², длина которой равна длине одного витка.
На практике эти движения достигаются на токарном станке, где острие резца соответствует данной точке.

Винтовая линия

Резец оставит на цилиндрической поверхности след - винтовую линию.
Винтовая линия может быть правой или левой. Правой винтовой линией называют линию, совершающую подъем вокруг своей оси против часовой стрелки, а левой - винтовую линию, совершающую подъем по часовой стрелке.
Правая цилиндрическая винтовая линия

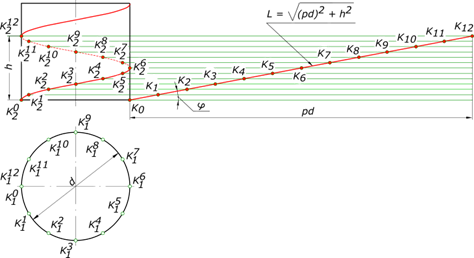
Винтовая линия

может быть построена, когда заданы ее элементы.
Винтовая линия характеризуется следующими элементами: шаг, виток и угол подъема.
Шагом винтовой линии называется расстояние между смежными витками, измеренное вдоль образующей кругового цилиндра.
Витком называют винтовую линию, описанную точкой за один оборот образующей вокруг оси кругового цилиндра. Длина витка равна L.
Углом подъема винтовой линии называют отношение tg(φ)= h/(pd), тогда φ = arctg(φ), где d - диаметр цилиндра, p=3,14.

Винтовая линия может быть получена на конической поверхности

Винтовая линия

В этом случае, точка совершает равномерно-поступательное движение вдоль образующей прямого кругового конуса, а сама образующая SA вращается вокруг его оси с постоянной угловой скорости.
Расстояние между точками смежных витков, измеренное параллельно оси конуса (например между точками A₀K₈), является шагом h конической винтовой линии.
Проекция винтовой линии на фронтальной плоскости проекций представляет собой синусоиду с затухающим колебанием (затухающей волной), а на горизонтальной - спираль Архимеда.
При построении развертки боковой поверхности конуса винтовая линия развернется в спираль, а конус - в сектор, угол при вершине которого равен φ= 360°×(h/L), а длина дуги радиуса R, соответствующая углу φ, равна 2πR.