Давление в жидкости и газе. Уравнение неразрывности. Уравнение Бернулли.

Давление в жидкостях: жидкость практически не сжимаема. Давление которое воздействует на закрытую в сосуде жидкость, распространяется по всем направлениям равномерно. Давление внутри жидкости везде одинаково.Давление в газах: газы — это тоже тела, и они имеют вес. 1 м3 воздуха весит примерно 1,29 кг. Молекулы газа отталкиваются друг от друга. Поэтому газы занимают в отведенном для них пространстве весь объем и создают давление на плоскостях, ограничивающих это пространство. Между молекулами газа много свободного пространства. Поэтому газы можно легко сжимать. При сжимании газа температура его повышается.

Неразрывности уравнение в гидродинамике, одно из уравнений гидродинамики, выражающее закон сохранения массы для любого объёма движущейся жидкости (газа). В переменных Эйлера имеет вид:

Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

6. Преобразование Галилея в классической механике. Постулаты СТО и преобразования Лоренца. Следствия СТО.

Преобразования Галилея - в классической механике преобразования координат и времени при переходе от одной инерциальной системы отсчета (ИСО) к другой. Термин был предложен Филиппом Франком в 1909 году. Преобразования Галилея подразумевают одинаковость времени во всех системах отсчета («абсолютное время») и выполнение принципа относительности (принцип относительности Галилея).

Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе (и даже больших), преобразования Галилея приближенно верны с очень большой точностью.

Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.

Инерциальная система отсчёта (ИСО) — это такая система, относительно которой объект, не подверженный внешним воздействиям, движется равномерно и прямолинейно. Событием называется любой физический процесс, который может быть локализован в пространстве, и имеющий при этом очень малую длительность. Другими словами, событие полностью характеризуется координатами (x, y, z) и моментом времени t. Примерами событий являются: вспышка света, положение материальной точки в данный момент времени и т. п.

Принцип относительности: ключевым для аксиоматики специальной теории относительности является принцип относительности, утверждающий равноправие инерциальных систем отсчёта. Это означает, что все физические процессы в инерциальных системах отсчёта описываются одинаковым образом.

Для этого необходимо рассмотреть три инерциальные системы S1, S2 и S3. Пусть скорость системы S2 относительно системы S1 равна v ₁, скорость системы S3 относительно S2 равна v ₂, а относительно S1, соответственно, v ₃. Записывая последовательность преобразований (S2, S1), (S3, S2) и (S3, S1), можно получить следующее равенство:

Преобразования (S2, S1) (S3, S2) имеют вид:

где γ₁ = γ(v ₁), и т.д. Подстановка (x ₂, t ₂) из первой системы во вторую, даёт:

Второе равенство является записью преобразований между системами S3 и S1. Если приравнять коэффициенты при x ₁ в первом уравнении системы и при t ₁ во втором, то:

Разделив одно уравнение на другое, несложно получить искомое соотношение.

Существование обратного преобразования между ИСО, отличающегося от прямого только заменой знака относительной скорости, позволяет найти функцию:

.

В силу принципа относительности две инерциальные системы отсчёта S и S' полностью равноправны. Поэтому должно существовать обратное преобразование от S' к S, в котором перед скоростью должен быть знак минус:

Во втором равенстве подставлено прямое преобразование:

и учтено, что Воспользовавшись свойством чётности γ(v) (аксиома изотропности), несложно получить, что . При извлечении квадратного корня необходимо выбрать знак плюс, чтобы, например, время событий, происходящих в точке x=0, были положительными t ' = γ(v) t при t > 0 (время "течёт" в одну сторону).

Таким образом, с точностью до произвольной константы α, получается явный вид преобразований между двумя ИСО. О численном значении константы α и её знаке без обращения к эксперименту ничего сказать нельзя ^[14]. Если α > 0, то удобно ввести обозначение α = 1 / c ². Тогда преобразования принимают следующий вид:

и называются преобразованиями Лоренца.

Различная запись преобразования Лоренца

Пусть координатные оси двух инерциальных систем отсчёта S и S' параллельны друг другу, (t, x,y, z) — время и координаты некоторого события, наблюдаемого относительно системы S, а (t',x',y',z') — время и координаты того же события относительно системы S'. Если система S' движется равномерно и прямолинейно со скоростью v относительно S, то справедливы преобразования Лоренца:

где c -скорость света. При скоростях много меньше скорости света () преобразования Лоренца переходят в преобразования Галилея:

Подобный предельный переход является отражением принципа соответствия, согласно которому более общая теория (СТО) имеет своим предельным случаем менее общую теорию (в данном случае — классическую механику).

Преобразования Лоренца можно записать в векторном виде, когда скорость систем отсчёта направлена в произвольном направлении (не обязательно вдоль оси x):

где 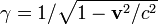— фактор Лоренца, и — радиус-векторы события относительно систем S и S'.