ОСНОВНЫЕ ПРИНЦИПЫ ПРОГРАММИРОВАНИЯ В СРЕДЕ MATHCAD
Методические указания

Волгоград
УДК 004.43
Рецензент
канд. техн. наук доцент В.И. Капля
Издается по решению редакционно-издательского совета
Волгоградского государственного технического университета
Белова С.В. Основные принципы программирования в среде Mathcad: [ Электронный ресурс ]: методические указания/ С.В. Белова// Сборник «Методические указания» Выпуск 5.-Электрон. текстовые дан.(1файл:600 Kb) – Волжский: ВПИ (филиал) ВолгГТУ, 2011.-Систем. требования:Windows 95 и выше; ПК с процессором 486+; CD-ROM.
Рассмотрены основные конструкции встроенного языка математического пакета Mathcad и их применение для программирования линейных, разветвляющихся и циклических алгоритмов.
Предназначены для студентов бакалавриата, обучающихся по направлению 240100.62 «Химическая технология». CD-ROM
ÓВолгоградский
государственный технический
университет, 2011 Ó Волжский
политехнический институт, 2011
ОГЛАВЛЕНИЕ
ОГЛАВЛЕНИЕ. 3
1. ЦЕЛЬ РАБОТЫ.. 4
2. СОЗДАНИЕ ПРОГРАММЫ.. 4
2.1. Описание программы - функции. 5
2.2. Оператор локального присваивания. 6
2.3. Вызов программы-функции. 7
3. ПРОГРАММИРОВАНИЕ ЛИНЕЙНЫХ АЛГОРИТМОВ.. 8
4. ПРОГРАММИРОВАНИЕ РАЗВЕТВЛЯЮЩИХСЯ АЛГОРИТМОВ.. 9
4.1. Условная функция if 11
4.2. Условный оператор if 11
5. ПРОГРАММИРОВАНИЕ ЦИКЛИЧЕСКИХ АЛГОРИТМОВ.. 15
5.1. Цикл с параметром FOR.. 15
5.2. Цикл с предусловием WHILE. 18
5.3. Вложенные циклы.. 21
7. ОПЕРАТОР ПРЕРЫВАНИЯ BREAK И ОПЕРАТОР ПРОДОЛЖЕНИЯ CONTINUE 22
8. ОПЕРАТОР ВОЗВРАТА RETURN И ОПЕРАТОР ОБРАБОТКИ ОШИБОК ON ERROR.. 23
9. ЗАДАНИЯ ПО ЛАБОРАТОРНОЙ РАБОТЕ. 24
9.1. Линейные алгоритмы.. 24
9.2. Разветвляющиеся алгоритмы.. 25
9.3. Циклические алгоритмы.. 28
ЛИТЕРАТУРА.. 30
ЦЕЛЬ РАБОТЫ
Формирование и отработка навыков программирования линейных, разветвляющихся и циклических алгоритмов в среде Mathcad.
СОЗДАНИЕ ПРОГРАММЫ
Все MathCAD-программы строятся как программы-функции. Результатом программы-функции может быть число, вектор или матрица. Программирование состоит в том, что сначала в документе размещается описание программы-функции, а затем для ее выполнения обращаются к ней по имени.
Для записи программ в MathCAD’e предусмотрена специальная панель инструментов – Программирование (рис. 2.1), которую можно вызвать на экран из меню Вид – Панели инструментов – Программирование. Операторы программы нельзя набирать с клавиатуры, их необходимо вводить нажатием соответствующих кнопок панели Программирование, либо использовать сочетания клавиш, которые приведены в тексте всплывающей подсказки.

Рис. 2.1.Панель инструментов Программирование
Ниже в таблице 2.1 приведены операторы, находящиеся на панели программирования.
Таблица 2.1. Кнопки панели Программирование
| Команда
| Функция
|
| Add Line
| Добавляет новую строку в программном блоке
|

| Символ локального присваивания
|
| if
| Условный оператор if
|
| otherwise
| Оператор, который выполняется в том случае, если условие оператора if ложное
|
| for
| Оператор цикла с параметром
|
| while
| Оператор цикла с условием
|
| break
| Оператор прерывания
|
| continue
| Оператор продолжения
|
| return
| Оператор возврата
|
| on error
| Оператор обработки ошибок
|
Вызов программы-функции
Для выполнения программы-функции необходимо обратиться к ней по имени с указанием списка фактических параметров и нажать клавишу «=». Оператор «=» используется для вывода на экран значений переменных и результатов вычисления выражений.
<имя программы-функции>(список фактических параметров)
Для каждого формального параметра при вызове программы-функции задается фактический параметр, значение которого должно быть определено. Именно с фактическими параметрами выполняются вычисления в программе-функции.
Фактическими параметрами могут быть константы, переменные, массивы. Между фактическими и формальными параметрами должно быть соответствие по количеству, типу и порядку следования. Имена фактических параметров при вызове программы-функции могут не совпадать с именами ее формальных параметров.
Примеры обращений к программе-функции f(x) (рис. 2.3):

При вызове программы-функции в качестве фактических параметров используются константа 7, переменная х и выражение (r+5), в третьем случае вызов программы-функции осуществляется в операторе присваивания. Переменная t, используемая при вызове программы-функции f(x) никак не связана с локальной переменной t, используемой внутри программы-функции. Локальный характер таких переменных позволяет использовать для их идентификаторов те же имена, что и у переменных документа. Однако лучше этого не делать и использовать разные имена для локальных переменных программы-функции и для переменных документа.
Для передачи данных внутрь программы-функции можно использовать как механизм параметров, так и описанные ранее переменные документа. Если в описании программы-функции отсутствует список формальных параметров, то и при ее вызове будет отсутствовать список фактических параметров, данные в программу-функцию передаются через имена переменных, определенных выше текста программы-функции. Эти переменные передаются в программу как значения и не изменяются, если в программе-функции им присваиваются другие значения (рис. 2.4).

Рис. 2.4. Передача в программу-функцию переменных документа
Хотя значение переменной х изменилось внутри программы-функции, вне ее описания переменная х сохранила свое прежнее значение.
Условная функция if
Эта функция записывается в виде (символы if вводятся с клавиатуры):
if (<логич. выраж.>, <выражение1>, <выражение2>)
Функция принимает значение выражения 1, если логическое выражение равно 1 и значение выражения 2, если логическое выражение равно 0.
Например: X← if (A > B, Y, Z) или if (A > B, X ← Y, X ← Z)
Пример 4.1. Вычислить значение переменной y..

Описание программы-функции и обращение к ней:

Можно использовать и такой вариант решения примера:

Условный оператор if
Структура условного оператора: <выражение> if <условие>
Действие оператора if начинается с проверки условия. Если оно истинно (равно 1), то возвращается значение выражения слева от оператора if. Это соответствует условной структуре, называемой ЕСЛИ – ТО.
Для вставки условного оператора в программу необходимо (рис. 4.3):
- ввести имя программы-функции со списком формальных параметров и символ “:”;
- щелкнуть кнопку Add line панели Программирование ина ней кнопку условного оператора if;
- справа от оператора if ввести условие, слева от if выражение, которое будет выполняться, если условие истинно; если в программе предусматриваются дополнительные условия, следует повторно нажать кнопку Add Line и ввести их аналогично, используя оператор if или otherwise.

Рис. 4.3. Вставка условного оператора
Для получения условной структуры ЕСЛИ–ТО–ИНАЧЕ используется оператор otherwise, который выполняется в том случае, если условие оператора if ложное.Для вставки оператора otherwise необходимо выделить поле, стоящее после оператора if, щелкнуть на кнопке otherwise панели Программирование и в поле оператора otherwise ввести соответствующее выражение.

Решим пример 4.1, используя в программе условный оператор if.
Блок-схема алгоритма:

Описание программы-функции и обращение к ней:

Пример 4.2. Вычислить значения полинома M(x) в зависимости от значения переменной y при x = 0,7.
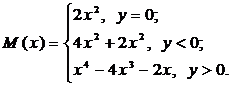
Блок-схема алгоритма решения примера:

Описание программы-функции и обращение к ней имеет вид:

При программировании сложных разветвляющихся алгоритмов возникает необходимость выполнить несколько операторов и при выполнении и при невыполнении условия в операторе if. В этом случае для добавления дополнительных строк необходимо выделить поле 1 условного оператора и/или поле слева от оператора otherwise и щелкнуть повторно на кнопке Add line панели Программирование.

Пример 4.3. Даны числа a, b, c. Удвоить эти числа, если a≥b≥c и заменить их абсолютными значениями, если это не так.
Блок-схема алгоритма решения примера:

Описание и вызов программы-функции приведены на рис. 4.4. Входными параметрами являются переменные a, b, и с. Выходным параметром является вектор v, элементы которого содержат новые значения переменных a, b, c.

Рис. 4.4. Реализация алгоритма примера 4.5
Пример 4.4. Даны произвольные числа a, b, c. Если нельзя построить треугольник с такими длинами сторон, то вывести об этом сообщение, иначе вывести сообщение о виде треугольника.
Описание программы-функции и обращение к ней:

Цикл с параметром FOR
Оператор цикла for служит для организации циклов с заданным числом повторений. Параметр такого цикла задается дискретной переменной (называемой также ранжированной переменной).

Рис. 5.1. Блок-схема цикла for
Последовательность действий для вставки оператора цикла for:
- ввести имя программы-функции, список формальных параметров и символ “:”;
- щелкнуть на кнопке for панели Программирование. На экране появятся поля для ввода, изображенные на рис. 5.2:

Рис. 5.2. Вставка оператора цикла for
- в первое поле ввести имя параметра цикла, например i;
- во второе поле диапазон значений параметра цикла, например: i1.. i2 (двоеточие между i1 и i2 набирается клавишей точка с запятой);
- в нижнее третье поле вводятся операторы тела цикла. Для добавления дополнительных операторов в тело цикла щелкните на кнопке Add line.
Операторы тела цикла, будут выполняться столько раз, сколько переменная i изменяет своё значение от i1 до i2 с шагом step. Если значение i1 + step не задано, то шаг изменения переменной, по умолчанию равен +1:

Пример 5.1. Вычислить: 
Блок-схема алгоритма решения примера:
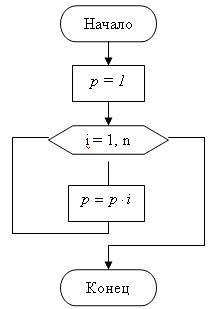
Описание и вызов программы-функции:

Пример 5.2. Вычислить: 
Описание и вызов программы-функции:

Пример 5.3. Дана последовательность  где i=1, 2,..., n. Подсчитать число четных элементов и число отрицательных элементов последовательности.
где i=1, 2,..., n. Подсчитать число четных элементов и число отрицательных элементов последовательности.

Пример 5.4. Вычислить значения функции  при изменении аргумента х от -1 до 2 с шагом 0.5 и сформировать из этих значений вектор y.
при изменении аргумента х от -1 до 2 с шагом 0.5 и сформировать из этих значений вектор y.
Блок-схема алгоритма решения примера:

Описание программы-функции и обращение к ней имеет вид:


Формальные параметры программы-функции Func используются для задания диапазона и шага изменения переменной x. Переменная i определяет текущее значение индекса элемента вектора y.
Цикл с предусловием WHILE
Цикл while называется с предусловием, т. к. проверка условия осуществляется перед каждым выполнением тела цикла. Используется, если число повторений цикла заранее неизвестно.
Выполнение оператора цикла while начинается с проверки условия. Если оно истинно, то выполняются операторы тела цикла, затем вновь проверятся условие и т. д. Как только на очередном шаге окажется, что условие ложное, то выполнение цикла завершится. Цикл while может ни разу не выполниться, если условие в самом начале ложное.
В блок-схеме цикл while изображается так, как показано на рис. 5.3.

Рис. 5.3. Блок-схема цикла while
Ввод оператора цикла while осуществляется аналогично вводу цикла for, после нажатия кнопки while панели Программирование на экране появляются элементы, показанные на рис. 5.4. В первое поле введите условие выполнения цикла, и в нижнее поле операторы тела цикла. Если в теле цикла более одного оператора, то нужно воспользоваться кнопкой Add Line для добавления дополнительных операторов в тело цикла.

Рис. 5.4. Вставка оператора цикла while
В теле цикла должен присутствовать хотя бы один оператор, изменяющий условие цикла так, чтобы цикл через некоторое число итераций завершился, иначе цикл будет выполняться бесконечно.
Пример 5.4. Найти первый отрицательный член последовательности 
Блок-схема алгоритма решения примера:

Описание и вызов программы-функции:

Пример 5.5. Вычислить значения функции  при изменении аргумента х от -1 до 3 с шагом 0.5 и сформировать из этих значений вектор y.
при изменении аргумента х от -1 до 3 с шагом 0.5 и сформировать из этих значений вектор y.
Эта задача уже была рассмотрена, но с использованием цикла For, решим ее с циклом While.
Описание и вызов программы-функции:

Пример 5.6. Найти количество и сумму цифр заданного натурального числа.Описание и вызов программы-функции:

В данной программе используются две функции:
· mod – выдаёт остаток при делении x на y.
· trunc – выдает целую часть z, удаляя дробную часть.
Пример 5.7. Составить программу для вычисления суммы членов бесконечного ряда с точностью до члена ряда  .
.

При этом вычисление текущего члена ряда выполнить по формуле: 
 -текущий член ряда,
-текущий член ряда,  - предыдущий член ряда.
- предыдущий член ряда.
Итерационным называется вычислительный процесс, в котором для определения последующего значения переменной используется её предыдущее значение. При использовании итерационных процессов реализуется метод последовательных приближений. Циклом управляет заданная погрешность вычислений e. Если на очередной итерации погрешность ≥e, то цикл продолжается для вычисления последующего приближённого значения результата, иначе происходит выход из цикла.
Описание и вызов программы-функции:

Вложенные циклы
Если телом цикла является циклическая структура, то такой цикл называется вложенным или сложным. Алгоритм со структурой вложенных циклов – это алгоритм, содержащий цикл, внутри которого размещены один или несколько других циклов.
Цикл, содержащий в себе другой цикл, называют внешним. Цикл, содержащийся в теле другого цикла, называют внутренним. Параметры внешнего и внутреннего циклов изменяются не одновременно и обозначаются различными переменными.
Простейший случай вложенных циклов – двойной. В этом случае один цикл помещается внутри другого. Различные варианты вложенных циклов:

Пример 6.1. Вычислить  .
.
Описание и вызов программы-функции:

Работа вложенного цикла заключается в следующем: сначала задаётся первое значение параметра внешнего цикла i, затем управление передаётся внутреннему циклу и параметр внутреннего цикла j принимает по очереди все значения. Когда выполнение внутреннего цикла окончено, задаётся второе значение параметра внешнего цикла и вновь полностью выполняется внутренний цикл. Процесс повторяется до тех пор, пока параметр внешнего цикла не примет все значения.
ЗАДАНИЯ ПО ЛАБОРАТОРНОЙ РАБОТЕ
Линейные алгоритмы
1. Составить программу для вычисления периметра и площади прямоугольного треугольника по длинам двух катетов.
2. Заданы координаты трех вершин треугольника (x1, y1), (х2, y2), (x3, y3). Составить программу для вычисления площади и периметра треугольника.
3. Составить программу для вычисления площади треугольника по длинам двух сторон треугольника и углу между ними.
4. Дана длина ребра куба. Составить программу для вычисления объема куба и площади его боковой поверхности.
5. Даны катеты прямоугольного треугольника. Составить программу для вычисления гипотенузы и площади прямоугольного треугольника.
6. Смешано V1 литров воды температуры t1 c V2 литрами воды температуры t2. Составить программу для вычисления объема и температуры образовавшейся смеси.
7. Дана сторона равностороннего треугольника. Составить программу для вычисления площади этого треугольника.
8. Дана гипотенуза и катет прямоугольного треугольника. Составить программу для вычисления второго катета и радиуса вписанной окружности.
9. Известна длина окружности. Составить программу для вычисления площади круга, ограниченного этой окружностью.
10. Составить программу для вычисления длины окружности, если задана площадь соответствующего круга.
11. Составить программу вычисления поверхности и объёма усечённого конуса.
12. Составить программу для вычисления медиан треугольника со сторонами a, b, с.
13. Составить программу для вычисления площади равностороннего треугольника, периметр которого равен P.
14. Дан радиус круга R. Составить программу для вычисления разности площадей квадрата и круга, который вписан в данный квадрат.
15. Составить программу для вычисления площади прямоугольника со сторонами a, b и площадь ромба, если его диагонали равны соответственно a и b.
16. Составить программу для вычисления площади равнобедренной трапеции по заданным величинам оснований, и угла при большем основании.
17. Составить программу для вычисления объёма пирамиды, основанием которой является треугольник со сторонами a, b, с.
18. Даны два числа x и y. Составить программу для вычисления полусуммы этих чисел и произведения модулей этих чисел.
19. Даны два неотрицательных числа a и b. Составить программу для вычисления среднего арифметического и среднего геометрического этих чисел.
20. Треугольник задан величинами своих углов и радиусом описанной окружности. Составить программу для вычисления сторон треугольника.
21. Составить программу для вычисления высоты треугольника со сторонами а, b, с.
22. Составить программу для вычисления площади круга, вписанного в треугольник с заданными сторонами а, b, с.
23. Составить программу вычисления объема цилиндра и конуса, которые имеют одинаковую высоту h и одинаковый радиус основания r.
Разветвляющиеся алгоритмы
1. Даны целое число k и вещественные числа a, b, c. Составить программу вычисления переменной y в зависимости от значения k:

2. Даны целое число t и вещественное число x. Составить программу вычисления переменной P в зависимости от значения t:

3. Даны целое число a и вещественные числа b, c, x. Составить программу вычисления переменной y в зависимости от значения а:

4. Даны целое число a и вещественные числа b, c, x. Составить программу вычисления переменной y в зависимости от значения а:

5. Даны целые числа a и i. Составить программу вычисления переменной y по формуле в зависимости от значения а:

6. Даны целые числа a и i. Составить программу вычисления переменной y по формуле в зависимости от значения а:

7. Даны целое число t и вещественное число x. Составить программу вычисления переменной P по формуле в зависимости от значения t:

8. Даны целое число k и вещественные числа a, b, c. Составить программу вычисления переменной y в зависимости от значения k:

9. Даны три целых числа a, b, c. Возвести в квадрат отрицательные числа и в третью степень — положительные.
10. Даны вещественные числа a, b, c. Получить: min(a, b, c).
11. Значения переменных x, y, z поменять местами так, чтобы они оказались упорядоченными по возрастанию.
12. Даны две переменные целого типа a и b. Если их значения не равны, то присвоить каждой переменной сумму этих значений, а если равны, то присвоить переменным нулевые значения.
13. Даны две переменные целого типа a и b. Если их значения не равны, то присвоить каждой переменной максимальное из этих значений, а если равны, то присвоить переменным нулевые значения.
14. Даны три переменные x, y, z. Если их значения упорядочены по убыванию, то удвоить их; в противном случае заменить значение каждой переменной на противоположное.
15. Даны три целых числа x, y, z. Найти среднее из них. Средним назовём число, которое больше наименьшего из данных чисел, но меньше наибольшего.
16. Составьте программу нахождения произведения двух наибольших из трёх введённых с клавиатуры чисел x, y, z.
17. Даны вещественные числа x, y (x ¹y). Меньшее из этих двух чисел заменить их полусуммой, а большее – их удвоенным произведением.
18. Даны три вещественных числа x, y, z. Возвести в квадрат те из них, значения которых неотрицательны.
19. Даны целые числа x и y. Если числа не равны, то заменить каждое из них одним и тем же числом, равным большему из исходных, а если равны, то заменить числа нулями.
20. Заданы три целых числа x, y, z. Если x<0, то определить р как максимальное из трёх чисел. Если x³0, то определить р как минимальное из трёх чисел.
21. Найти произведение двух наибольших из трех заданных чисел, используя при этом не более двух сравнений.
22. Составить программу, вычисляющую произведение двух наибольших из четырех заданных чисел.
23. Для заданных значений x, e, z, t вычислить значение переменной V:
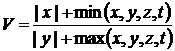 .
.
Циклические алгоритмы
1. Вычислить первое значение функции 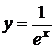 , удовлетворяющее неравенству
, удовлетворяющее неравенству  при изменении x от 1 с шагом 0,01. Определить, на каком шаге это произойдет.
при изменении x от 1 с шагом 0,01. Определить, на каком шаге это произойдет.
2. Найти и напечатать максимальное значение функции  на отрезке [0, 7] для x, изменяющегося с шагом 0,12.
на отрезке [0, 7] для x, изменяющегося с шагом 0,12.
3. Вычислить десятое значение функции 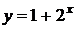 при изменении аргумента от 1 с шагом 0,1, которое было получено после достижения условия
при изменении аргумента от 1 с шагом 0,1, которое было получено после достижения условия  .
.
4. Рассчитать значения функции  на отрезке [-1,1] с шагом 0,01. Предусмотреть блокировку от деления на 0.
на отрезке [-1,1] с шагом 0,01. Предусмотреть блокировку от деления на 0.
5. Рассчитать первое значение функции  , удовлетворяющее условию
, удовлетворяющее условию  , где a - заданная величина, x изменяется от –1 с шагом 0,3.
, где a - заданная величина, x изменяется от –1 с шагом 0,3.
6. Составить программу вычисления функции  на отрезке
на отрезке
[-10, 10] с шагом 0,12.
7. Подсчитать сумму положительных значений функции  при изменении x на отрезке [-5,5] с шагом 0,2.
при изменении x на отрезке [-5,5] с шагом 0,2.
8. Вычислить третье значение функции 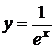 , удовлетворяющее условию Y<10-3 при изменении x от 5 с шагом 1.
, удовлетворяющее условию Y<10-3 при изменении x от 5 с шагом 1.
9. Рассчитать функцию 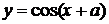 на отрезке [1,10] c шагом h. Определить сумму значений y, больших значения С.
на отрезке [1,10] c шагом h. Определить сумму значений y, больших значения С.
10. Найти сумму значений функции  , где x изменяется от –1,2 с шагом 1,1. Суммирование прекратить при выполнении условия
, где x изменяется от –1,2 с шагом 1,1. Суммирование прекратить при выполнении условия 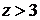 .
.
11. Дано натуральное число. Найти сумму цифр этого числа, верно ли, что число начинается и заканчивается одной и той же цифрой.
12. Дано натуральное число. Найти произведение цифр этого числа, верно ли, что в данном числе нет цифры А.
13. Дано натуральное число. Найти количество цифр этого числа, верно ли, что данное число заканчивается на нечётную цифру.
14. Дано натуральное число. Найти количество чётных цифр этого числа, верно ли, что данная цифра А встречается в числе более двух раз.
15. Дано натуральное число. Найти первую и последнюю цифру числа, верно ли, что сумма цифр данного числа равна А.
16. Дано натуральное число. Сколько раз данная цифра А встречается в данном числе, верно ли, что в данном числе сумма цифр больше В, а само число делится на В.
17. Дано число. Посчитать сумму цифр, стоящих на чётных местах числа.
18. Дано число. Посчитать произведение цифр числа, которые кратны 3.
19. Дано число. Посчитать разность между первым и последним числом.
20. Определить количество трёхзначных натуральных чисел, сумма цифр которых равна n (1≤ n ≤27).
21. Дано натуральное число n. Составить программу для вычисления суммы чисел вида  (i=1, 2,…, n), которые являются нечетными числами.
(i=1, 2,…, n), которые являются нечетными числами.
22. Найти сумму первых n членов ряда  .
.
23. Найти произведение десяти членов ряда  .
. 
24. Найти сумму первых n членов ряда  где x – любое число.
где x – любое число.
25. Вычислить сумму элементов ряда с точностью до заданного e=0,001.

26. Даны действительное число a и натуральное число n. Вычислить:

27. Даны два числа m и n. Если m2>n2, вычислить и напечатать сумму ряда чисел:  с точностью 10-3, иначе отпечатать m и n.
с точностью 10-3, иначе отпечатать m и n.
28. Найти сумму первых n членов ряда: 
29. Дано натуральное число n. Вычислить: 
30. Вычислить: 
31. Дано вещественное число a. Найти среди чисел  первое, большее а.
первое, большее а.
32. Вычислить сумму n элементов ряда:

33. Дано c и d. Если  , вычислить значения функции
, вычислить значения функции  , где x изменяется на отрезке от –2 до 2 с шагом 0,25. Если
, где x изменяется на отрезке от –2 до 2 с шагом 0,25. Если  , вычислить переменную
, вычислить переменную  .
.
34. Вычислить  .
.
ЛИТЕРАТУРА
1. Ю.Е. Воскобойников, В.Ф. Очков Программирование и решение задач в пакете MathCAD. Учебное пособие. – Новосибирск: НГАСУ, 2002, 136 с.
2. Ю. Е. Воскобойников, Т. Н. Воскобойникова Программирование в математическом пакете MathCAD. Методические указания. – Новосибирск: НГАСУ, 1999 г.
3. Д. Гурский, Е. Турбина Вычисления в Mathcad – 12. – СПб.: Питер, 2006, 544 с.
4. http://www.mathcading.com/Glava6/index6.html
Учебное издание
Светлана Владимировна Белова
В среде Mathcad
Методические указания
План электронных изданий 2011 г. Поз. № 52В
Подписано на «Выпуск в свет» 15.06.2011 г. Уч-изд. л. 1,92.
На магнитоносителе.
Волгоградский государственный технический университет.
400131, г. Волгоград, пр. Ленина, 28, корп. 1.
ОСНОВНЫЕ ПРИНЦИПЫ ПРОГРАММИРОВАНИЯ В СРЕДЕ MATHCAD
Методические указания

Волгоград
УДК 004.43
Рецензент
канд. техн. наук доцент В.И. Капля
Издается по решению редакционно-издательского совета
Волгоградского государственного технического университета
Белова С.В. Основные принципы программирования в среде Mathcad: [ Электронный ресурс ]: методические указания/ С.В. Белова// Сборник «Методические указания» Выпуск 5.-Электрон. текстовые дан.(1файл:600 Kb) – Волжский: ВПИ (филиал) ВолгГТУ, 2011.-Систем. требования:Windows 95 и выше; ПК с процессором 486+; CD-ROM.
Рассмотрены основные конструкции встроенного языка математического пакета Mathcad и их применение для программирования линейных, разветвляющихся и циклических алгоритмов.
Предназначены для студентов бакалавриата, обучающихся по направлению 240100.62 «Химическая технология». CD-ROM
ÓВолгоградский
государственный технический
университет, 2011 Ó Волжский
политехнический институт, 2011
ОГЛАВЛЕНИЕ
ОГЛАВЛЕНИЕ. 3
1. ЦЕЛЬ РАБОТЫ.. 4
2. СОЗДАНИЕ ПРОГРАММЫ.. 4
2.1. Описание программы - функции. 5
2.2. Оператор локального присваивания. 6
2.3. Вызов программы-функции. 7
3. ПРОГРАММИРОВАНИЕ ЛИНЕЙНЫХ АЛГОРИТМОВ.. 8
4. ПРОГРАММИРОВАНИЕ РАЗВЕТВЛЯЮЩИХСЯ АЛГОРИТМОВ.. 9
4.1. Условная функция if 11
4.2. Условный оператор if 11
5. ПРОГРАММИРОВАНИЕ ЦИКЛИЧЕСКИХ АЛГОРИТМОВ.. 15
5.1. Цикл с параметром FOR.. 15
5.2. Цикл с предусловием WHILE. 18
5.3. Вложенные циклы.. 21
7. ОПЕРАТОР ПРЕРЫВАНИЯ BREAK И ОПЕРАТОР ПРОДОЛЖЕНИЯ CONTINUE 22
8. ОПЕРАТОР ВОЗВРАТА RETURN И ОПЕРАТОР ОБРАБОТКИ ОШИБОК ON ERROR.. 23
9. ЗАДАНИЯ ПО ЛАБОРАТОРНОЙ РАБОТЕ. 24
9.1. Линейные алгоритмы.. 24
9.2. Разветвляющиеся алгоритмы.. 25
9.3. Циклические алгоритмы.. 28
ЛИТЕРАТУРА.. 30
ЦЕЛЬ РАБОТЫ
Формирование и отработка навыков программирования линейных, разветвляющихся и циклических алгоритмов в среде Mathcad.
СОЗДАНИЕ ПРОГРАММЫ
Все MathCAD-программы строятся как программы-функции. Результатом программы-функции может быть число, вектор или матрица. Программирование состоит в том, что сначала в документе размещается описание программы-функции, а затем для ее выполнения обращаются к ней по имени.
Для записи программ в MathCAD’e предусмотрена специальная панель инструментов – Программирование (рис. 2.1), которую можно вызвать на экран из меню Вид – Панели инструментов – Программирование. Операторы программы нельзя набирать с клавиатуры, их необходимо вводить нажатием соответствующих кнопок панели Программирование, либо использовать сочетания клавиш, которые приведены в тексте всплывающей подсказки.

Рис. 2.1.Панель инструментов Программирование
Ниже в таблице 2.1 приведены операторы, находящиеся на панели программирования.
Таблица 2.1. Кнопки панели Программирование
| Команда
| Функция
|
| Add Line
| Добавляет новую строку в программном блоке
|

| Символ локального присваивания
|
| if
| Условный оператор if
|
| otherwise
| Оператор, который выполняется в том случае, если условие оператора if ложное
|
| for
| Оператор цикла с параметром
|
| while
| Оператор цикла с условием
|
| break
| Оператор прерывания
|
| continue
| Оператор продолжения
|
| return
| Оператор возврата
|
| on error
| Оператор обработки ошибок
|

















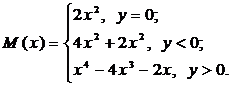














 где i=1, 2,..., n. Подсчитать число четных элементов и число отрицательных элементов последовательности.
где i=1, 2,..., n. Подсчитать число четных элементов и число отрицательных элементов последовательности.
 при изменении аргумента х от -1 до 2 с шагом 0.5 и сформировать из этих значений вектор y.
при изменении аргумента х от -1 до 2 с шагом 0.5 и сформировать из этих значений вектор y.









 .
.

 -текущий член ряда,
-текущий член ряда,  - предыдущий член ряда.
- предыдущий член ряда.

 .
.








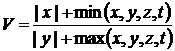 .
.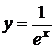 , удовлетворяющее неравенству
, удовлетворяющее неравенству  при изменении x от 1 с шагом 0,01. Определить, на каком шаге это произойдет.
при изменении x от 1 с шагом 0,01. Определить, на каком шаге это произойдет. на отрезке [0, 7] для x, изменяющегося с шагом 0,12.
на отрезке [0, 7] для x, изменяющегося с шагом 0,12.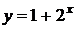 при изменении аргумента от 1 с шагом 0,1, которое было получено после достижения условия
при изменении аргумента от 1 с шагом 0,1, которое было получено после достижения условия  .
. на отрезке [-1,1] с шагом 0,01. Предусмотреть блокировку от деления на 0.
на отрезке [-1,1] с шагом 0,01. Предусмотреть блокировку от деления на 0. , удовлетворяющее условию
, удовлетворяющее условию  , где a - заданная величина, x изменяется от –1 с шагом 0,3.
, где a - заданная величина, x изменяется от –1 с шагом 0,3. на отрезке
на отрезке при изменении x на отрезке [-5,5] с шагом 0,2.
при изменении x на отрезке [-5,5] с шагом 0,2.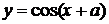 на отрезке [1,10] c шагом h. Определить сумму значений y, больших значения С.
на отрезке [1,10] c шагом h. Определить сумму значений y, больших значения С. , где x изменяется от –1,2 с шагом 1,1. Суммирование прекратить при выполнении условия
, где x изменяется от –1,2 с шагом 1,1. Суммирование прекратить при выполнении условия 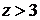 .
. (i=1, 2,…, n), которые являются нечетными числами.
(i=1, 2,…, n), которые являются нечетными числами. .
. .
. 
 где x – любое число.
где x – любое число.

 с точностью 10-3, иначе отпечатать m и n.
с точностью 10-3, иначе отпечатать m и n.


 первое, большее а.
первое, большее а.
 , вычислить значения функции
, вычислить значения функции  , где x изменяется на отрезке от –2 до 2 с шагом 0,25. Если
, где x изменяется на отрезке от –2 до 2 с шагом 0,25. Если  , вычислить переменную
, вычислить переменную  .
. .
.


