1. Основные понятия. Линейным дифференциальным уравнением п-го порядка называется уравнение вида
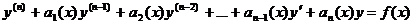 (1)
(1)
Здесь функции 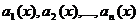 и f(x) заданы и непрерывны в некотором промежутке (а, b).
и f(x) заданы и непрерывны в некотором промежутке (а, b).
Уравнение (1) называется линейным неоднородным, или уравнением с правой частью. Если же f(x)≡0, то уравнение называется линейным однородным. Однородное уравнение с той же левой частью, что и данное неоднородное, называется соответствующим ему.
Зная одно частное решение у1 линейного однородного уравнения, можно с помощью линейной замены искомой функции 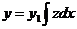 понизить порядок, а следовательно, и порядок соответствующего неоднородного уравнения на единицу. Полученное уравнение (n-1) -го порядка относительно z также является линейным.
понизить порядок, а следовательно, и порядок соответствующего неоднородного уравнения на единицу. Полученное уравнение (n-1) -го порядка относительно z также является линейным.
676. Дано уравнение 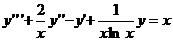 и известно частное решение y1 = ln(х) соответствующего однородного уравнения. Понизить порядок уравнения.
и известно частное решение y1 = ln(х) соответствующего однородного уравнения. Понизить порядок уравнения.
Решение:
Воспользуемся подстановкой 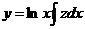 , где z — новая неизвестная функция. Тогда, подставляя соответствующие производные
, где z — новая неизвестная функция. Тогда, подставляя соответствующие производные
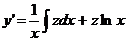 ,
, 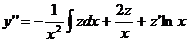 ,
, 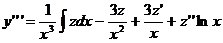
в данное уравнение, получим уравнение второго порядка
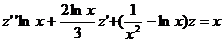
Примечание. Отметим, что применяя указанную подстановку к линейному уравнению второго порядка и учитывая, что линейное уравнение первого порядка интегрируется в квадратурах, можно проинтегрировать в квадратурах всякое линейное уравнение второго порядка, если известно одно частное решение соответствующего однородного уравнения.
677. Проинтегрировать уравнение 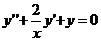 , имеющее частное решение
, имеющее частное решение 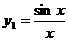
Решение. Произведем замену 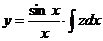 ;
;
тогда
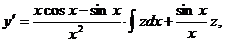
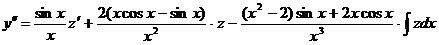
Получаем уравнение
Следовательно,
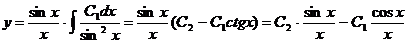
678. Понизить порядок и проинтегрировать уравнение у" sin2x= 2у, имеющее частное решение у=ctgх.
679. Уравнение 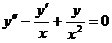 имеет частное решение у = х. Понизить порядок и проинтегрировать это уравнение.
имеет частное решение у = х. Понизить порядок и проинтегрировать это уравнение.
680. Уравнение 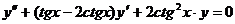 имеет частное решение у=sinх. Понизить порядок и проинтегрировать это уравнение.
имеет частное решение у=sinх. Понизить порядок и проинтегрировать это уравнение.
2. Линейные однородные уравнения. Одним из замечательных свойств линейных уравнений является то, что общее решение таких уравнений можно найти по их известным частным решениям. Приведем теорему о структуре общего решения линейного однородного уравнения.
Теорема. Если у1, у2,..., yn—линейно независимые частные решения уравнения
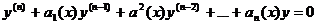 .
.
то у = С 1 y 1 + С2 y2 +... + Сn yn есть общее решение этого уравнения (С1, С 2,..., С n — произвольные постоянные).
П р и м е ч а н и е. Функции у1 (х), у2(х),..., yn(х) называются линейно независимыми в промежутке (а, b), если они не связаны никаким тождеством
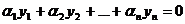 .
.
где α 1, α 2,..., α n —какие-нибудь постоянные, не равные нулю одновременно. Для случая двух функций это условие можно сформулировать и так: две функции y 1 (х) и y 2 (х) линейно независимы, если их отношение не является постоянной величиной: y 1/ y 2 ≠ соnst. Например: 1) у1=х, y 2=х2— линейно независимы; 2) у1=еx, у1=е-x — линейно независимы; 3) у1=2езх, у 2 =5езx — линейно зависимы.
Достаточным условием линейной независимости п функций, непрерывных вместе со своими производными до (п— 1)-го порядка в промежутке (а, b), является то, что определитель Вронского (вронскиан) W [у 1, y 2,..., yn ]этих функций не равен нулю ни в одной точке промежутка (а, b), т. е.
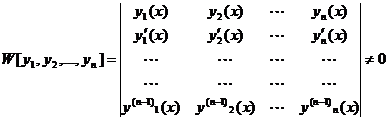
Если данные п функций являются частными решениями линейного однородного дифференциального уравнения n-го порядка, то это условие (необращение в нуль) является не только достаточным, но и необходимым условием линейной независимости этих п решений.
Вронскиан л решений линейного однородного уравнения n-го порядка
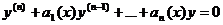 связан с первым коэффициентом этого уравнения а1(х) формулой Лиувилля — Остроградского:
связан с первым коэффициентом этого уравнения а1(х) формулой Лиувилля — Остроградского:
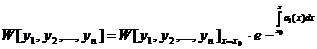
Совокупность n решений линейного однородного уравнения n-го порядка, определенных и линейно независимых в промежутке(а, b), называется фундаментальной системой решений этого уравнения.
Для линейного однородного дифференциального уравнения второго порядка
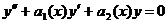
фундаментальная система состоит из двух линейно независимых решений у1 (х) и y2(х), его общее решение находится по формуле
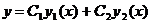
Если для такого уравнения известно одно частное решение у1 (х), то второе его решение, линейно независимое с первым, можно найти по формуле
(являющейся следствием формулы Лиувилля—Остроградского)
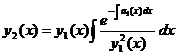
Это дает возможность интегрировать линейные однородные уравнения второго порядка, для которых известно одно частное решение, сразу, не прибегая к понижениюих порядка.
Так, в примере 677 для уравнения 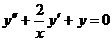 известно решение
известно решение
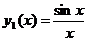 Найдем по приведенной выше формуле второе решение:
Найдем по приведенной выше формуле второе решение:
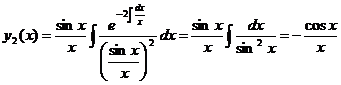
Поэтому общее решение данного уравнения имеет вид
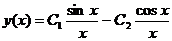
Рекомендуем решить этим способом примеры 678—680.
681. Показать, что 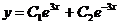 является общим решением уравнения у"— 9y=0.
является общим решением уравнения у"— 9y=0.
Решение. Подстановкой в уравнение легко убедиться в том, что функции у1=е3x и у2=е-3x являются его решениями. Эти частные решения линейно независимы, так как 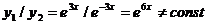 , а потому они составляют фундаментальную систему решений и, следовательно,
, а потому они составляют фундаментальную систему решений и, следовательно, 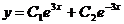 —общее решение.
—общее решение.
682. Дано уравнение у'"—у'=0. Составляют ли фундаментальную систему решений функции е x, е -x, сh х, являющиеся, как легко проверить, решениями этого уравнения?
Решение. Для проверки линейной независимости этих решений вычислим вронскиан:
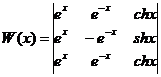
Этот определитель равен нулю, так как элементы 1-й и 3-й строк одинаковы. Следовательно, данные функции линейно зависимы, а потому составить общее решение по этим частным решениям нельзя. Тот же результат можно получить быстрее, поскольку 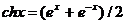 и, следовательно, данные три функции линейно зависимы.
и, следовательно, данные три функции линейно зависимы.
683. Уравнению у"—у=0 удовлетворяют два частных решения y1=shx, y2=chx. Составляют ли они фундаментальную систему?
684. Можно ли составить общее решение уравнения
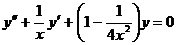 (x≠0) по двум его частным решениям
(x≠0) по двум его частным решениям 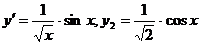
Установить, являются ли линейно независимыми в промежутке своего существования следующие функции:
685. x+1, 2x+1, х+2.
686. 2x2+1, x2-1, х+2.
687. 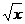 ,
, 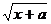 ,
, 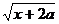 .
.
688. ln(2х), ln(3x), ln(4x).



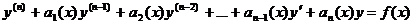 (1)
(1)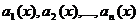 и f(x) заданы и непрерывны в некотором промежутке (а, b).
и f(x) заданы и непрерывны в некотором промежутке (а, b).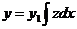 понизить порядок, а следовательно, и порядок соответствующего неоднородного уравнения на единицу. Полученное уравнение (n-1) -го порядка относительно z также является линейным.
понизить порядок, а следовательно, и порядок соответствующего неоднородного уравнения на единицу. Полученное уравнение (n-1) -го порядка относительно z также является линейным.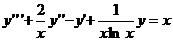 и известно частное решение y1 = ln(х) соответствующего однородного уравнения. Понизить порядок уравнения.
и известно частное решение y1 = ln(х) соответствующего однородного уравнения. Понизить порядок уравнения.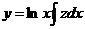 , где z — новая неизвестная функция. Тогда, подставляя соответствующие производные
, где z — новая неизвестная функция. Тогда, подставляя соответствующие производные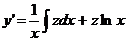 ,
, 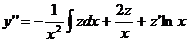 ,
, 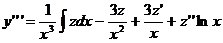
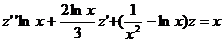
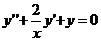 , имеющее частное решение
, имеющее частное решение 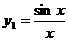
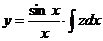 ;
;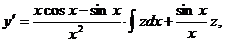
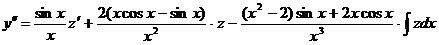
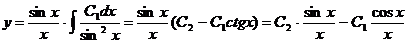
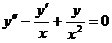 имеет частное решение у = х. Понизить порядок и проинтегрировать это уравнение.
имеет частное решение у = х. Понизить порядок и проинтегрировать это уравнение.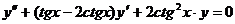 имеет частное решение у=sinх. Понизить порядок и проинтегрировать это уравнение.
имеет частное решение у=sinх. Понизить порядок и проинтегрировать это уравнение.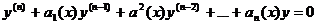 .
.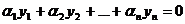 .
.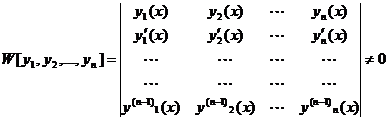
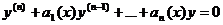 связан с первым коэффициентом этого уравнения а1(х) формулой Лиувилля — Остроградского:
связан с первым коэффициентом этого уравнения а1(х) формулой Лиувилля — Остроградского: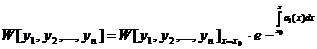
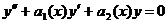
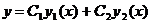
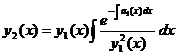
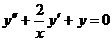 известно решение
известно решение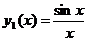 Найдем по приведенной выше формуле второе решение:
Найдем по приведенной выше формуле второе решение: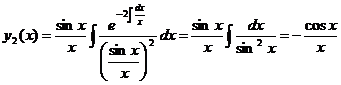
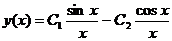
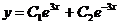 является общим решением уравнения у"— 9y=0.
является общим решением уравнения у"— 9y=0.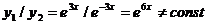 , а потому они составляют фундаментальную систему решений и, следовательно,
, а потому они составляют фундаментальную систему решений и, следовательно, 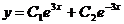 —общее решение.
—общее решение.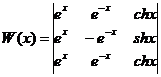
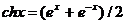 и, следовательно, данные три функции линейно зависимы.
и, следовательно, данные три функции линейно зависимы.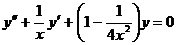 (x≠0) по двум его частным решениям
(x≠0) по двум его частным решениям 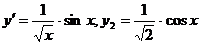
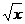 ,
, 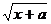 ,
, 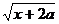 .
.

