Пусть 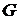 – связный нагруженный граф. Задача построения минимального остовного дерева заключается в том, чтобы из множества остовных деревьев найти дерево, у которого сумма длин ребер минимальна.
– связный нагруженный граф. Задача построения минимального остовного дерева заключается в том, чтобы из множества остовных деревьев найти дерево, у которого сумма длин ребер минимальна.
Приведем типичные случаи, когда возникает необходимость построения минимального остовного дерева графа.
а) Нужно соединить 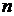 городов железнодорожными линиями (автомобильными дорогами, линиями электропередач, сетью трубопроводов и т.д.) так, чтобы суммарная длина линий или стоимость была бы минимальной.
городов железнодорожными линиями (автомобильными дорогами, линиями электропередач, сетью трубопроводов и т.д.) так, чтобы суммарная длина линий или стоимость была бы минимальной.
б) Требуется построить схему электрической сети, в которой клеммы должны быть соединены с помощью проводов наименьшей общей длины.
Задачу построения минимального остовного дерева можно решить с помощью следующего алгоритма Краскала.
Алгоритм Краскала.
Шаг 1. Установка начальных значений. Вводится матрица длин ребер 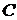 графа
графа 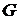 .
.
Шаг 2. Выбрать в графе 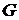 ребро минимальной длины. Построить граф
ребро минимальной длины. Построить граф 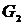 , состоящий из данного ребра и инцидентных ему вершин. Положить
, состоящий из данного ребра и инцидентных ему вершин. Положить 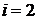 .
.
Шаг 3. Если 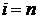 , где
, где 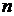 – число ребер графа, то закончить работу (задача решена), в противном случае перейти к шагу 4.
– число ребер графа, то закончить работу (задача решена), в противном случае перейти к шагу 4.
Шаг 4. Построить граф 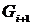 , добавляя к графу
, добавляя к графу 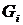 новое ребро минимальной длины, выбранное среди всех ребер графа
новое ребро минимальной длины, выбранное среди всех ребер графа 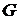 , каждое из которых инцидентно какой-нибудь вершине графа
, каждое из которых инцидентно какой-нибудь вершине графа 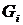 и одновременно инцидентно какой-нибудь вершине графа
и одновременно инцидентно какой-нибудь вершине графа 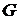 , не содержащейся в
, не содержащейся в 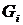 . Вместе с этим ребром включаем в
. Вместе с этим ребром включаем в 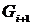 и инцидентную ему вершину, не содержащуюся в
и инцидентную ему вершину, не содержащуюся в 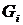 . Присваиваем
. Присваиваем 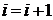 и переходим к шагу 3.
и переходим к шагу 3.
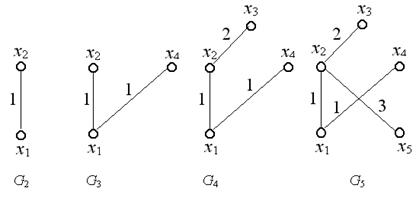
Пример. Найдем минимальное остовное дерево для графа, изображенного на рис. 36.
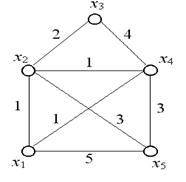
Рис. 36
Шаг 1. Установка начальных значений. Введем матрицу длин ребер 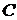 :
:
С = 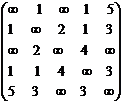 .
.
Шаг 2. Выберем ребро минимальной длины. Минимальная длина ребра равна единице. Таких ребер три: 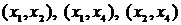 . В этом случае можно взять любое. Возьмем
. В этом случае можно взять любое. Возьмем 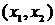 . Построим граф
. Построим граф 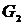 , состоящий из данного ребра и инцидентных ему вершин
, состоящий из данного ребра и инцидентных ему вершин 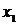 и
и 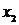 . Положим
. Положим 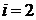 .
.
Шаг 3. Так как 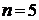 , то
, то 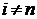 , поэтому переходим к шагу 4.
, поэтому переходим к шагу 4.
Шаг 4. Строим граф 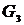 , добавляя к графу
, добавляя к графу 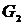 новое ребро минимальной длины, выбранное среди всех ребер графа
новое ребро минимальной длины, выбранное среди всех ребер графа 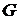 , каждое из которых инцидентно одной из вершин
, каждое из которых инцидентно одной из вершин 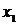 ,
, 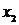 и одновременно инцидентно какой-нибудь вершине графа
и одновременно инцидентно какой-нибудь вершине графа 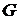 , не содержащейся в
, не содержащейся в 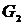 т. е. одной из вершин
т. е. одной из вершин 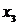 ,
, 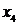 ,
, 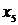 . Таким образом, нужно выбрать ребро минимальной длины из ребер
. Таким образом, нужно выбрать ребро минимальной длины из ребер 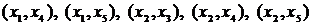 . Таких ребер длины единица два:
. Таких ребер длины единица два: 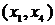 и
и 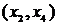 . Можно выбрать любое. Возьмем
. Можно выбрать любое. Возьмем 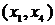 . Вместе с этим ребром включаем в
. Вместе с этим ребром включаем в  вершину
вершину 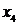 , не содержащуюся в
, не содержащуюся в 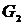 . Полагаем
. Полагаем 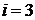 и переходим к шагу 3.
и переходим к шагу 3.
Шаг 3. Так как 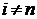 , поэтому переходим к шагу 4.
, поэтому переходим к шагу 4.
Шаг 4. Строим граф 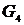 , добавляя к графу
, добавляя к графу 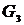 новое ребро минимальной длины из ребер
новое ребро минимальной длины из ребер 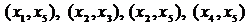 . Такое ребро длины два одно:
. Такое ребро длины два одно: 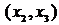 . Вместе с этим ребром включаем в
. Вместе с этим ребром включаем в 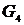 вершину
вершину 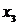 , не содержащуюся в
, не содержащуюся в 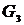 . Полагаем
. Полагаем 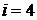 и переходим к шагу 3.
и переходим к шагу 3.
Шаг 3. Так как 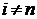 , поэтому переходим к шагу 4.
, поэтому переходим к шагу 4.
Шаг 4. Строим граф 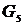 , добавляя к графу
, добавляя к графу 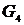 новое ребро минимальной длины из ребер
новое ребро минимальной длины из ребер 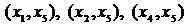 . Таких ребер длины три два:
. Таких ребер длины три два: 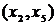 и
и 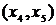 . Возьмем
. Возьмем 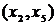 . Вместе с этим ребром включаем в
. Вместе с этим ребром включаем в  вершину
вершину 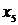 , не содержащуюся в
, не содержащуюся в 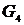 . Полагаем
. Полагаем 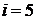 и переходим к шагу 3.
и переходим к шагу 3.
Шаг 3. Так как 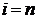 , то граф
, то граф 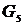 – искомое минимальное остовное дерево. Суммарная длина ребер равна
– искомое минимальное остовное дерево. Суммарная длина ребер равна 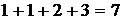 .
.
Процесс построения минимального остовного дерева изображен ниже.
7.10. Задачи для самостоятельного решения
1. Какое из двух утверждений верно?
а) ориентированный граф является частным случаем неориентированного графа;
б) неориентированный граф является частным случаем ориентированного графа.
2. Что характеризует сумма элементов столбца матрицы смежности неориентированного графа?
3. Что характеризует сумма элементов строки матрицы смежности неориентированного графа?
4. Что характеризует сумма элементов столбца матрицы смежности ориентированного графа?
5. Что характеризует сумма элементов строки матрицы смежности ориентированного графа?
6. Всегда ли матрица смежности симметрична относительно главной диагонали?
7. Как по матрице смежности определить число ребер неориентированного графа?
8. Как по матрице инцидентности, не рисуя граф, определить его матрицу смежности?
9. Какие из следующих утверждений являются правильными?
а) если матрица смежности несимметричная, то граф ориентированный;
б) если граф неориентированный, то матрица смежности симметричная;
в) если диагональные элементы матрицы смежности – нули, то граф неориентированный.
10. Может ли вершина, входящая в цикл графа, иметь степень, меньшую двух?
11. Как называется путь, у которого начало первой дуги совпадает с концом последней?
12. Как называется маршрут, у которого первая вершина совпадает с последней вершиной?
13. Какие из следующих матриц полностью задают граф?
а) матрица инцидентности; б) матрица связности;
в) матрица сильной связности; г) матрица смежности.
14. По какой матрице можно без дополнительных вычислений определить число компонент связности неориентированного графа?
а) матрице смежности; б) матрице инцидентности;
в) матрице связности.
15. Может ли число компонент связности графа превосходить число его вершин?
16. Верно или неверно утверждение, что в ориентированном графе с контурами минимальный путь может содержать контуры?
17. Как называется связный граф без циклов?
18. Сколько ребер имеет связный граф без циклов с 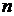 вершинами?
вершинами?
19. Чему равно наименьшее и наибольшее число ребер в связном графе без петель и кратных ребер с 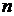 вершинами?
вершинами?
20. Чему равно наименьшее и наибольшее число ребер в графе без петель и кратных ребер с 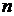 вершинами?
вершинами?
21. Верно или неверно утверждение, что минимальное остовное дерево может содержать циклы?
22. Сколько компонент связности может иметь дерево?
23. Можно ли построить дерево, все вершины которого имеют степень больше, чем единица?
24. Может ли матрица 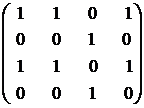 быть матрицей смежности неориентированного графа?
быть матрицей смежности неориентированного графа?
ЛИТЕРАТУРА
1. Хаусдорф Ф. Теория множеств. – 3-е изд., стер. – М.: КомКнига, 2006.
2. Москинова Г. И. Дискретная математика. Математика для менеджера в примерах и упражнениях. – М.: Логос, 2007.
3. Аляев Ю. А., Тюрин С. Ф. Дискретная математика и математическая логика: учебник. – М.: ФиС, 2006.
4. Оре О. Графы и их применение. – 3-е изд., стер. – М.: КомКнига, 2006.
5. Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. – М.: Физматлит, 2001, 2004.
6. Обработка нечеткой информации в системах принятия решения / А. Н. Борисов, А. В. Алексеев, Г. В. Меркулова и др. – М.: Радио и связь, 1989.
7. Кирсанов М. Н. Графы в Maple. Задачи, алгоритмы, программы. (Сер. «Информационные и компьютерные технологии»). – М.: Физматлит, 2007.
8. Кофман А. Введение в теорию нечетких множеств. – М.: Радио и связь, 1982.
9. Андерсон Дж. А. Дискретная математика и комбинаторика. – М.: Вильямс, 2004.
10. Кузнецов О. П. Дискретная математика для инженера. – 6 изд. СПб.: Лань, 2009.
11. Палий И. А. Дискретная математика: курс лекций. – М.: Эксмо, 2008.
12. Хаггарти Р. Дискретная математика для программистов. – М.: Техносфера, 2005.
13. Шапорев С. Д. Дискретная математика: курс лекций и практических занятий. – СПб.: БХВ-Петербург, 2007.
14. Яблонский С. В. Введение в дискретную математику. 4-е изд., стер. – М.: Высшая школа, 2003.
15. Поздняков С. Н., Рыбин С. В. Дискретная математика: учебник для вузов. 2-е изд., перераб. и допол. – М.: Академия, 2008.
16. Плотников А. Д. Дискретная математика. – 3-е изд., исп. и доп. – Минск: Новое знание, 2008.
17. Акимов О. Е. Дискретная математика: логика, группы, графы. – М.: Лаборатория Базовых Знаний, 2001.
18. Липский В. Комбинаторика для программистов. – М.: Мир, 1988.
19. Нефедов В. Н., Осипова В. А. Курс дискретной математики. – М.: Изд. – МАИ, 1992.
20. Новиков Ф. А. Дискретная математика для программистов. Учебник для вузов. 2-е изд.– СПб.: Питер, 2007.
21. Судоплатов С. В., Овчинникова В. В. Элементы дискретной математики. – М.: ИНФРА – М, Новосибирск: Изд-во НГТУ, 2002.
22. Иванов Б. И. Дискретная математика. – М., Физматлит, 2007.
23. Иванов Б. Н. Дискретная математика. Алгоритмы и программы: Учеб. пособие. (Сер. «Технический университет»). – М.: Лаборатория Базовых Знаний, 2003.
24. Тишин В. В. Дискретная математика в примерах и задачах. (Учебная литература для вузов). – СПб.: БХВ-Петербург, 2008.



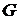 – связный нагруженный граф. Задача построения минимального остовного дерева заключается в том, чтобы из множества остовных деревьев найти дерево, у которого сумма длин ребер минимальна.
– связный нагруженный граф. Задача построения минимального остовного дерева заключается в том, чтобы из множества остовных деревьев найти дерево, у которого сумма длин ребер минимальна.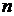 городов железнодорожными линиями (автомобильными дорогами, линиями электропередач, сетью трубопроводов и т.д.) так, чтобы суммарная длина линий или стоимость была бы минимальной.
городов железнодорожными линиями (автомобильными дорогами, линиями электропередач, сетью трубопроводов и т.д.) так, чтобы суммарная длина линий или стоимость была бы минимальной.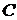 графа
графа 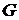 ребро минимальной длины. Построить граф
ребро минимальной длины. Построить граф 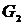 , состоящий из данного ребра и инцидентных ему вершин. Положить
, состоящий из данного ребра и инцидентных ему вершин. Положить 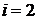 .
.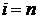 , где
, где 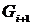 , добавляя к графу
, добавляя к графу 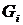 новое ребро минимальной длины, выбранное среди всех ребер графа
новое ребро минимальной длины, выбранное среди всех ребер графа 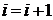 и переходим к шагу 3.
и переходим к шагу 3.
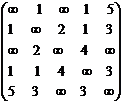 .
.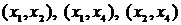 . В этом случае можно взять любое. Возьмем
. В этом случае можно взять любое. Возьмем 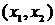 . Построим граф
. Построим граф 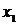 и
и 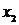 . Положим
. Положим 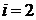 .
.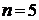 , то
, то 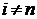 , поэтому переходим к шагу 4.
, поэтому переходим к шагу 4.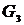 , добавляя к графу
, добавляя к графу 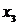 ,
, 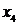 ,
, 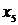 . Таким образом, нужно выбрать ребро минимальной длины из ребер
. Таким образом, нужно выбрать ребро минимальной длины из ребер 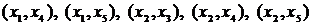 . Таких ребер длины единица два:
. Таких ребер длины единица два: 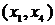 и
и 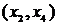 . Можно выбрать любое. Возьмем
. Можно выбрать любое. Возьмем 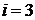 и переходим к шагу 3.
и переходим к шагу 3.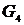 , добавляя к графу
, добавляя к графу 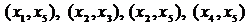 . Такое ребро длины два одно:
. Такое ребро длины два одно: 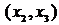 . Вместе с этим ребром включаем в
. Вместе с этим ребром включаем в 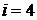 и переходим к шагу 3.
и переходим к шагу 3.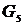 , добавляя к графу
, добавляя к графу 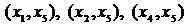 . Таких ребер длины три два:
. Таких ребер длины три два: 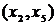 и
и 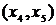 . Возьмем
. Возьмем 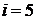 и переходим к шагу 3.
и переходим к шагу 3.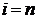 , то граф
, то граф 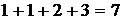 .
.
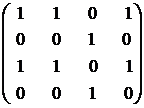 быть матрицей смежности неориентированного графа?
быть матрицей смежности неориентированного графа?


