Комплексные числа
Комплексное число – расширение понятие числа. Ранее мы представляли себе числа как прямую. С введением понятия комплексных чисел мы представляем число как плоскость, где одна прямая – ось реальных чисел, вторая – ось мнимых чисел. Таким образом, лежащая на первой прямой точка – реальное число, на второй – мнимое, не принадлежащая ни одной из них – комплексное число.
Комплексное число имеет вид a+bi, где а – реальное число, bi–мнимое.
Мнимое число в свою очередь состоит из реального числа bпомноженного на мнимую единицу i, представляющую собой 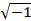 .
.
С комплексными числами можно выполнять действие, как то:
· Сложение и вычитание. В данном случае результатом будет комплексное число, коэффициенты aи bкоторого являются суммой или разностью коэффициентов aи bисходных чисел.
· Умножение. В данном случае числа перемножаются как произведение двух сумм.
· Деление. В данном случае числитель и знаменательно домножаются на знаменатель.
· Сравнение. Сравниваются значение aи bпопарно.
Свободные векторы, их сложение и умножение на число
Вектор – направленный отрезок.
Свободный вектор – вектор, который может свободно переноситься в пространстве. Таким образом, если в пространстве есть два вектора, модуль и направление которых одинаковы, а начало и конец не совпадают, то данные вектора являются равными.
При умножении вектора на число его модуль домножается на заданное число, направление остаётся прежним.
При сложении двух векторов получается вектор, координаты которого являются суммой координат исходных векторов. Это очень легко иллюстрировать при помощи стандартного метода треугольника – начало второго вектора переносится в конец первого. Результатом будет вектор, имеющий начало первого и конец второго.
Декартов базис, составляющие вектора по оси и его проекция на ось
Базис— множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов.
Декартов базис представляет собой набор векторов i,j,k, где каждый из представленных векторов является единичным положительным отрезком на осях x,y,z.
В данном случае любой вектор можно разложить по базису – представить его как сумму вышеуказанных векторов.
Проекция же вектора на ось в таком случае является количеством соответствующих единичных векторов.
Векторное произведение векторов
Векторное произведение векторов – произведение, дающее как результат вектор, перпендикулярный плоскости первых двух векторов. Причём длинна данного вектора будет равна произведению модулей первых двух векторов, помноженных на синус угла между ними.
Записывается как [a,b] или axb.
Геометрический смысл: даёт площадь параллелограмма, построенного на данных векторах.
Свойства:
· Если [a,b] равно c, то [b,a] равно –с.
· Свойство ассоциативности: c[a,b]=[ca,b]=[a,cb].
· Свойство дистрибутивности: [a+b,c]=[a,c]+[b,c].
· ТождествоЛагранжа: [a, [b,c]]=b(a,c)-c(a,b).
· 
· Векторное произведение вектора на самого себя (либо на коллинеарный себе вектор) даёт 0.
Прямая на плоскости
Формы записи прямой:
· Каноническая
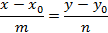
· Общая
Ax+By+C=0
· С угловым коэффициентом

Формула угла для двух прямых на плоскости:

Кривые второго порядка
Общее уравнение кривой второго порядка:

Где хотя бы один из параметров A,B,C не равен нулю.
Эллипс
Частный случай эллипса - круг.
Такая замкнутая кривая, что сумма расстояний от любой её точки до двух фокусов одинакова и равна 2а.
Формула эллипса (каноническая):

Где b2=a2-c2, а и b– большая и малая полуоси, c–полурасстояние между фокусами.

Где  – эксцентриситет (0<
– эксцентриситет (0<  <1).
<1).
Уравнение касательной:

Гипербола
Такая кривая, что модуль разности расстояний от любой её точки до двух фокусов является величиной постоянной и равно 2а.
Формула гиперболы (каноническая):

Где b2=a2-c2, а и b– реальная и мнимая полуоси, c–полурасстояние между фокусами.

Где  – эксцентриситет (
– эксцентриситет ( >1).]
>1).]
Асимптоты гиперболы:

Уравнение касательной:

Парабола
Множество точек на плоскости, равноудалённых от прямой (директрисы) и точки (фокусы).
Каноническое уравнение:

Где p – параметр параболы.
Уравнение касательной:

Поверхности второго порядка
Общее уравнение кривой второго порядка:

Где хотя бы один из параметров A,B,C,D,E,F не равен нулю.
Эллипсоид
Частный случай эллипсоида – сфера (все три оси одинаковы). 

Однополостный гиперболоид 

Двуполостный гиперболоид 

Эллиптический параболоид 

Гиперболический параболоид 

Цилиндр
Конус
13,14)Линейное пространство. Определение, примеры. Базис. Размерность. Разложение вектора по базису
Линейное пространство – математическая структура, которая формируется векторами.
В любом линейном пространстве есть 2 операции:
1. Сложение. Для любой суммы векторов есть существующий в пространстве результат.
2. Умножение на скаляр. Для любого умноженного на скаляр вектора есть существующий в пространстве результат.
На операции накладываются следующие условия:
1. 1·x=x
2. x+y=y+x
3. 
4. 
5. 
6. 
7. 
8. 
В каждом пространстве существует некоторая размерность – максимально возможный набор линейно независимых векторов. Любой другой вектор можно получить набором этих векторов, причём только одним.
Базис же является совокупностью этих векторов.
Примером линейных пространств можно привести двухмерное и трёхмерное Декартовы xyz.
Умножение матриц
При умножении матрицы Aна матрицу Bнеобходимо, чтобы число столбцов матрицы Aсовпадало с числом строк матрицы B. Только тогда можно умножать.
В таком случае результирующая матрица Cбудет иметь количество строк Aи столбцов B, а её числа будут результатом всех возможных перемножений строк Aна B.
Свойства:
§ 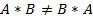
Бывают исключения, называемые коммутирующими матрицами.
§ 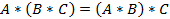
§ 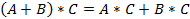
§ 
§ 
§ Det(A*B)=DetA*DetB
Обратная матрица
Матрица  называется обратной к матрице A, если
называется обратной к матрице A, если 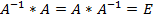

Где AdT– алгебраическое дополнение, транспонированное.
Примечание: алгебраическим дополнением для какого-либо элемента матрицы является определитель исходной матрицы свычеркнутыми строкой и столбцом исходной матрицы, в которых стоял данный элемент.
Теорема: для того, чтобы для матрицы существовала обратная, необходимо и достаточно, чтобы матрица имела определитель не равный нулю.
Док-во необходимости:
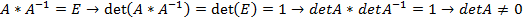
Док-во достаточности(док-во неверно!):
Пускай, B – алгебраическое дополнение матрицы A. ДомножимB на определитель A в минус первой степени.
Докажем, что  .
.
В таком случае, если вынести у B за скобку определитель в минус первой степени, то при произведении матриц мы получим на главной диагонали определители, а на всех остальных местах нули. Доможив на определитель, получим единичную матрицу.
Свойства обратной матрицы:
· 
· 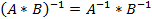
· 
Ранг матрицы
Наибольший порядок не равного нулю минора матрицы Aназывается рангом матрицы A.
Ранг не может превышать наименьшее из числа строк\столбцов матрицы.
СЛАУ, методы решения.
Система Линейных Алгебраических Уравнений (СЛАУ) может быть:
· Однородной (все свободные члены равны нулю) и Неоднородной.
· Совместной (система имеет одно или более решений) и Несовместной.
· Определённой (одно решение) и Неопределённой.
· Если решения двух систем одинаковы, то они называются Эквивалентными.
Матричный метод
В матричном методе любое СЛАУ представляется, как матричное уравнение  , где A–матрица коэффициентов, X–искомая матрица неизвестных и B–матрица свободных коэффициентов.
, где A–матрица коэффициентов, X–искомая матрица неизвестных и B–матрица свободных коэффициентов.
Таким образом,  .
.
Метод Крамера
Метод (или же правило) Крамера – следствие из матричного метода.
Здесь каждый из неизвестных аргументов представляется собой как определитель аргумента поделённый на определитель матрицы СЛАУ, где определитель аргумента – определитель матрицы СЛАУ, в который столбец, принадлежащий искомому аргументу, был заменён на столбец свободных коэффициентов.
Метод Гаусса
Метод Гаусса использует элементарные преобразования строк для получения из расширенной матрицы СЛАУ треугольной или диагональной расширенной матрицы СЛАУ, которая при домножении на матрицу неизвестных аргументов даёт решение.
Квадратичная форма
Пусть есть некоторое векторное пространство Lс базисом e1,e2…en.
Функция Q:  называется квадратичной формой, если её можно представить в виде Q(x)=
называется квадратичной формой, если её можно представить в виде Q(x)=  .
.
Матричная запись:
A= 
Q(x)=XTAX
25)Преобразование квадратичной формы к каноничному виду
Квадратичная форма канонична в случае, если  .
.
При ортогональном преобразовании квадратичная форма приводится к виду Q(x)=  , где
, где  Пример задачи:
Пример задачи:

Комплексные числа
Комплексное число – расширение понятие числа. Ранее мы представляли себе числа как прямую. С введением понятия комплексных чисел мы представляем число как плоскость, где одна прямая – ось реальных чисел, вторая – ось мнимых чисел. Таким образом, лежащая на первой прямой точка – реальное число, на второй – мнимое, не принадлежащая ни одной из них – комплексное число.
Комплексное число имеет вид a+bi, где а – реальное число, bi–мнимое.
Мнимое число в свою очередь состоит из реального числа bпомноженного на мнимую единицу i, представляющую собой 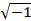 .
.
С комплексными числами можно выполнять действие, как то:
· Сложение и вычитание. В данном случае результатом будет комплексное число, коэффициенты aи bкоторого являются суммой или разностью коэффициентов aи bисходных чисел.
· Умножение. В данном случае числа перемножаются как произведение двух сумм.
· Деление. В данном случае числитель и знаменательно домножаются на знаменатель.
· Сравнение. Сравниваются значение aи bпопарно.
Свободные векторы, их сложение и умножение на число
Вектор – направленный отрезок.
Свободный вектор – вектор, который может свободно переноситься в пространстве. Таким образом, если в пространстве есть два вектора, модуль и направление которых одинаковы, а начало и конец не совпадают, то данные вектора являются равными.
При умножении вектора на число его модуль домножается на заданное число, направление остаётся прежним.
При сложении двух векторов получается вектор, координаты которого являются суммой координат исходных векторов. Это очень легко иллюстрировать при помощи стандартного метода треугольника – начало второго вектора переносится в конец первого. Результатом будет вектор, имеющий начало первого и конец второго.



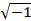 .
.
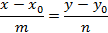





 – эксцентриситет (0<
– эксцентриситет (0<  <1).
<1).






















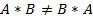
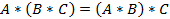
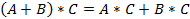


 называется обратной к матрице A, если
называется обратной к матрице A, если 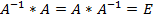

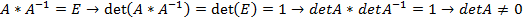
 .
.
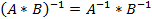

 , где A–матрица коэффициентов, X–искомая матрица неизвестных и B–матрица свободных коэффициентов.
, где A–матрица коэффициентов, X–искомая матрица неизвестных и B–матрица свободных коэффициентов. .
. называется квадратичной формой, если её можно представить в виде Q(x)=
называется квадратичной формой, если её можно представить в виде Q(x)=  .
.
 .
. , где
, где  Пример задачи:
Пример задачи:



