Конструктивное определение рациональных чисел Q дано в схеме 1.2. Приведем аксиоматическое построение множества рациональных чисел. Суть аксиоматического построения в том, что оно выдвигает такой минимум правил (аксиом), который обеспечивает построение множества Q со всеми операциями, перечисленными в п.1.2. Поэтомуаксиоматика рациональных чисел должна содержать правила, определяющие действия с операциями сложения и вычитания, умножения и деления, сравнения чисел, и связь между этими операциями.
Определение 1.
Множество Q называется множеством рациональных чисел, а его элементы - рациональными числами, если выполняется следующий комплекс условий, называемый аксиоматикой рациональных чисел:
Аксиомы операции сложения.
Для всякой упорядоченной пары х,у элементов из Q определен некоторый элемент х+у Î Q, называемый суммой х и у. При этом выполняются следующие условия:
1. (Существование нуля) Существует элемент 0 (нуль) такой, что для любого х Î Q
х + 0 = 0 + х = х.
2. Для любого элемента х Î Q существует элемент - х Î Q (противоположный х) такой, что
х + (-х) = (-х) + х = 0.
3. (Коммутативность) Для любых х,у Î Q
 х + у = у + х
х + у = у + х
4. (Ассоциативность) Для любых х, у, z Î Q
х + (у + z) = (х + у) + z
Аксиомы операции умножения.
Для всякой упорядоченной пары х,у элементов из Q определен некоторый элемент ху Î Q, называемый произведением х и у. При этом выполняются следующие условия:
5. (Существование единичного элемента) Существует элемент 1Î Q такой, что для любого х Î Q
х ×1 = 1× х = х
6. Для любого элемента х Î Q, (х¹ 0) существует обратный элемент х -1 ¹ 0 такой, что
х×х -1 = х-1×х = 1
7. (Ассоциативность) Для любых х, у, z Î Q
х× (у× z) = (х× у)× z
8. (Коммутативность) Для любых х, у Î Q
х × у = у× x
Аксиома связи сложения и умножения.
9. (Дистрибутивность) Для любых х, у, z Î Q
(х+у) × z = x × z+у × z
Аксиомы порядка.
Всякие два элемента х, у, Î Q вступают в отношение сравнения £. При этом выполняются следующие условия:
10. (х 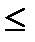 у) Ù (у
у) Ù (у 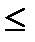 x)
x)  x = у
x = у
11. (х 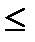 у) Ù (у
у) Ù (у 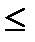 z)
z) 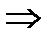 x
x 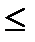 z
z
12. Для любых х, у Î Q либо х < у, либо у < x.
Отношение < называется строгим неравенством,
Отношение = называется равенством элементов из Q.
Аксиома связи сложения и порядка.
13. Для любых x, y, z Î Q, (x £ y) Þ x + z £ y + z
Аксиома связи умножения и порядка.
14. (0 £ x)Ç(0 £ y) Þ (0 £ x ´ y)
Аксиома непрерывности Архимеда.
15. Для любых a > b > 0 существует m Î N и n Î Q такие, что m ³ 1, n < b и a = mb + n.
Следствие.
Аксиомы множества рациональных чисел Q позволяют:
1. Построить систематическую запись рациональных чисел при помощи конечного алфавита (цифровых символов) в виде К -ичной системы.
2. Определить алгоритмы реализации операций ±, ´,:, £ в систематической записи рациональных чисел в выбранной К -ичной системе.



 х + у = у + х
х + у = у + х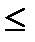 у) Ù (у
у) Ù (у  x = у
x = у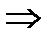 x
x 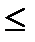 z
z


